Physics307L F07:People/Trujillo/LAB NOTEBOOK/071003
Raw Data Files
- File:Dwell20ms.asc
- File:Dwell40ms.asc
- File:Dwell80ms.asc
- File:Dwell100ms.asc
- File:Dwell200ms.asc
- File:Dwell400ms.asc
- File:Dwell800ms.asc
- File:Dwell1s.asc
- File:Dwell10s.asc
10ms
Oct 03 2007 03:07:41 am Elt: 000000 Seconds. Real Time: 000000
ID: No spectrum identifier defined
Memory Size: 16384 Chls Conversion Gain: 1024 Adc Offset: 0000 Chls
Chn Counts ROI
0, 0, 000
1, 0, 000
2, 0, 000
3, 0, 000
4, 0, 000
5, 0, 000
6, 0, 000
7, 0, 000
8, 0, 000
9, 0, 000
10, 0, 000
11, 0, 000
12, 0, 000
13, 0, 000
14, 0, 000
15, 0, 000
16, 0, 000
17, 0, 000
18, 0, 000
19, 0, 000
20, 0, 000
21, 0, 000
22, 0, 000
23, 0, 000
24, 0, 000
25, 0, 000
26, 0, 000
27, 0, 000
28, 0, 000
29, 0, 000
30, 0, 000
31, 0, 000
32, 0, 000
33, 0, 000
34, 0, 000
35, 0, 000
36, 0, 000
37, 0, 000
38, 0, 000
39, 0, 000
40, 0, 000
41, 0, 000
42, 0, 000
43, 0, 000
44, 0, 000
45, 0, 000
46, 0, 000
47, 0, 000
48, 0, 000
49, 0, 000
50, 0, 000
51, 0, 000
52, 0, 000
53, 0, 000
54, 0, 000
55, 0, 000
56, 0, 000
57, 0, 000
58, 0, 000
59, 0, 000
60, 0, 000
61, 0, 000
62, 0, 000
63, 0, 000
64, 1, 000
65, 0, 000
66, 0, 000
67, 0, 000
68, 0, 000
69, 0, 000
70, 0, 000
71, 0, 000
72, 0, 000
73, 0, 000
74, 0, 000
75, 0, 000
76, 0, 000
77, 0, 000
78, 0, 000
79, 0, 000
80, 0, 000
81, 0, 000
82, 0, 000
83, 0, 000
84, 0, 000
85, 0, 000
86, 0, 000
87, 0, 000
88, 0, 000
89, 0, 000
90, 0, 000
91, 0, 000
92, 0, 000
93, 0, 000
94, 0, 000
95, 0, 000
96, 0, 000
97, 0, 000
98, 0, 000
99, 0, 000
100, 0, 000
101, 0, 000
102, 0, 000
103, 0, 000
104, 0, 000
105, 0, 000
106, 1, 000
107, 0, 000
108, 0, 000
109, 0, 000
110, 0, 000
111, 0, 000
112, 0, 000
113, 0, 000
114, 0, 000
115, 0, 000
116, 0, 000
117, 0, 000
118, 0, 000
119, 0, 000
120, 0, 000
121, 0, 000
122, 0, 000
123, 0, 000
124, 0, 000
125, 0, 000
126, 0, 000
127, 0, 000
128, 0, 000
129, 0, 000
130, 0, 000
131, 0, 000
132, 0, 000
133, 0, 000
134, 0, 000
135, 0, 000
136, 0, 000
137, 0, 000
138, 0, 000
139, 0, 000
140, 0, 000
141, 0, 000
142, 0, 000
143, 0, 000
144, 0, 000
145, 0, 000
146, 1, 000
147, 0, 000
148, 0, 000
149, 0, 000
150, 0, 000
151, 0, 000
152, 0, 000
153, 0, 000
154, 0, 000
155, 0, 000
156, 0, 000
157, 0, 000
158, 0, 000
159, 0, 000
160, 0, 000
161, 0, 000
162, 0, 000
163, 0, 000
164, 0, 000
165, 0, 000
166, 0, 000
167, 1, 000
168, 0, 000
169, 0, 000
170, 0, 000
171, 0, 000
172, 0, 000
173, 0, 000
174, 0, 000
175, 0, 000
176, 0, 000
177, 0, 000
178, 0, 000
179, 0, 000
180, 0, 000
181, 0, 000
182, 0, 000
183, 0, 000
184, 0, 000
185, 0, 000
186, 0, 000
187, 0, 000
188, 0, 000
189, 0, 000
190, 0, 000
191, 0, 000
192, 0, 000
193, 0, 000
194, 0, 000
195, 0, 000
196, 0, 000
197, 0, 000
198, 0, 000
199, 0, 000
200, 0, 000
201, 0, 000
202, 0, 000
203, 0, 000
204, 0, 000
205, 0, 000
206, 0, 000
207, 0, 000
208, 0, 000
209, 0, 000
210, 0, 000
211, 0, 000
212, 0, 000
213, 0, 000
214, 2, 000
215, 0, 000
216, 0, 000
217, 0, 000
218, 1, 000
219, 0, 000
220, 0, 000
221, 0, 000
222, 0, 000
223, 0, 000
224, 2, 000
225, 0, 000
226, 0, 000
227, 0, 000
228, 0, 000
229, 0, 000
230, 0, 000
231, 0, 000
232, 0, 000
233, 0, 000
234, 0, 000
235, 0, 000
236, 0, 000
237, 0, 000
238, 0, 000
239, 0, 000
240, 0, 000
241, 0, 000
242, 0, 000
243, 0, 000
244, 0, 000
245, 0, 000
246, 0, 000
247, 0, 000
248, 0, 000
249, 0, 000
250, 0, 000
251, 2, 000
252, 0, 000
253, 0, 000
254, 0, 000
255, 0, 000
==Octave script for analysis & plotting==
{{SJK comment|label=01:21, 22 October 2007 (CDT)|comment=I had never heard of Octave before, so found [http://en.wikipedia.org/wiki/GNU_Octave a description on wikipedia]. Are you happy with it? Is it easy to use if you don't know matlab? In any case, thanks for posting your analysis code! I hope to have some time to check it out...}}
chop off the first ten lines of the data files before use
rename variable and filenames as necessary. Probably only needs minor tweeks so that it can run in matlab.
<pre><nowiki>#octave
#a sort of diary of commands to automate the data processing day to day
#some of octave's functions do not work in matlab,and vice
#versa. Some functions may work, but not in the same way
#Most things work, though.
#Tomas Mondragon
load LAB3_D10.ASC; #The load function is intended
load LAB3_D20.ASC; #to read files saved by octave.
load LAB3_D40.ASC; #Load can also read .mat files,
load LAB3_D80.ASC; #but only versions saved by matlab
load LAB3_D100.ASC; #version 4. It can also read text files.
load LAB3_D200.ASC; #if no variable name info is in the file
load LAB3_D400.ASC; #it names the variable after the file name
load LAB3_D800.ASC;
load LAB3_D1S.ASC;
load LAB3_D10S.ASC;
dwell10ms=LAB3_D10(:,2); #load put what was on LAB3_D10.ASC into the
dwell20ms=LAB3_D20(:,2); #variable LAB3_D10. I only care about the second
dwell40ms=LAB3_D40(:,2); #column of the data, so here I extract it to an
dwell80ms=LAB3_D80(:,2); #appropriately named variable.
dwell100ms=LAB3_D100(:,2);
dwell200ms=LAB3_D200(:,2); #The first column of LAB3_D10 is the channel number
dwell400ms=LAB3_D400(:,2); #but a more appropriate name would be the bin index.
dwell800ms=LAB3_D800(:,2); #The second column is a count of how many events fell
dwell1s=LAB3_D1S(:,2); #into the bin. The third column isn't important for this
dwell10s=LAB3_D10S(:,2); #experiment, but knowing what it is will allow one to take
#advantage PCA3's region of interest feature. It just marks
#where one has marked ROI's. for example, 4 indicates the bin or channel
#lies within ROI 4
#idea:use max(dwell10s) as max bin for all so grapfh are same x scale
#[y,x]=hist(data,bincenters) is a a function that sets up bins whose values are centered
#at the values given by the vector bincenter and counts the number of times the values in
#data fall into each of the bins. y contains the frequncy counts and x contains the
#corresponding bin index. bar(x,y) will plot the histogram of data. In general, x=bincenters,
#so one can shorten [y,x]=hist(data,bincenters) to y=hist(data,bincenters) and use
#bar(bincenters,y) to plot the same thing.
bincenters=0:max(dwell10s);
freq10ms=hist(dwell10ms,bincenters);
freq20ms=hist(dwell20ms,bincenters);
freq40ms=hist(dwell40ms,bincenters);
freq80ms=hist(dwell80ms,bincenters);
freq100ms=hist(dwell100ms,bincenters);
freq200ms=hist(dwell200ms,bincenters);
freq400ms=hist(dwell400ms,bincenters);
freq800ms=hist(dwell800ms,bincenters);
freq1s=hist(dwell1s,bincenters);
freq10s=hist(dwell10s,bincenters);
#plots. press any key to move to next plot
bar(bincenters,freq10ms)
title("frequency counts for dwell time=10ms")
xlabel("number of events occuring during dwell time")
ylabel("frequency count")
pause
replot
bar(bincenters,freq20ms)
title("frequency counts for dwell time=20ms")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
pause
replot
bar(bincenters,freq40ms)
title("frequency counts for dwell time=40ms")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
pause
replot
bar(bincenters,freq80ms)
title("frequency counts for dwell time=80ms")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
pause
replot
bar(bincenters,freq100ms)
title("frequency counts for dwell time=100ms")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
pause
replot
bar(bincenters,freq200ms)
title("frequency counts for dwell time=200ms")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
pause
replot
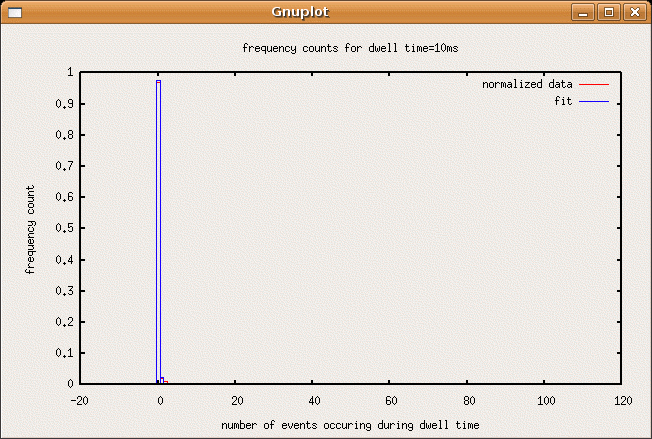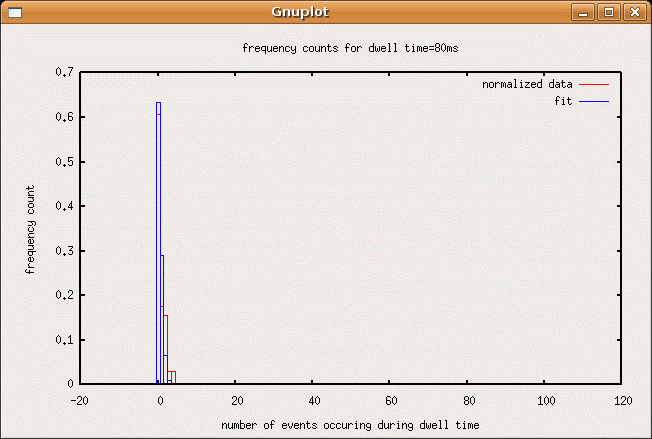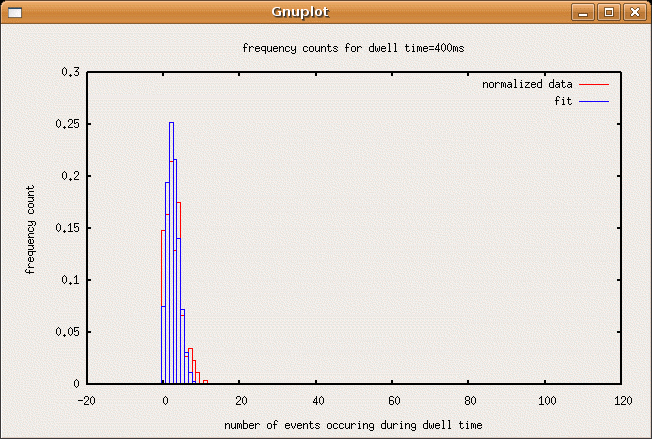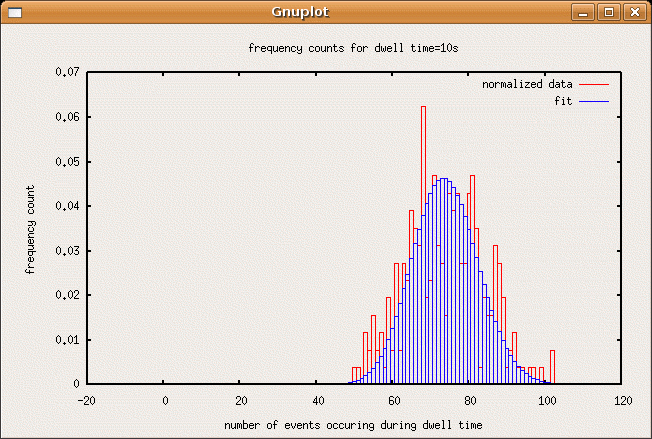
bar(bincenters,freq400ms)
title("frequency counts for dwell time=400ms")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
pause
replot
bar(bincenters,freq800ms)
title("frequency counts for dwell time=800ms")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
pause
replot
bar(bincenters,freq1s)
title("frequency counts for dwell time=1s")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
pause
replot
bar(bincenters,freq10s)
title("frequency counts for dwell time=10s")
%xlabel("number of events occuring during dwell time")
%ylabel("frequency count")
Compilation of plots
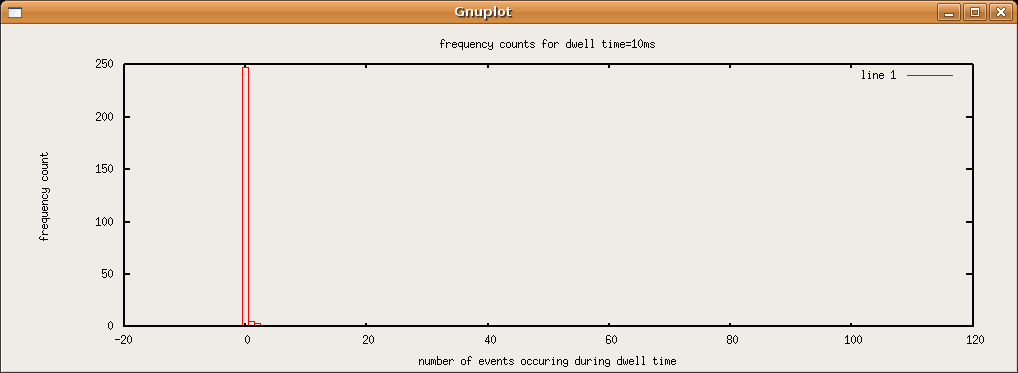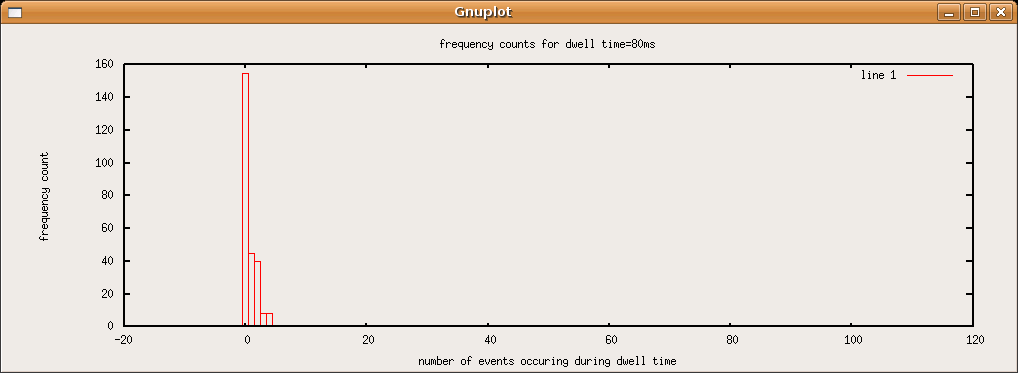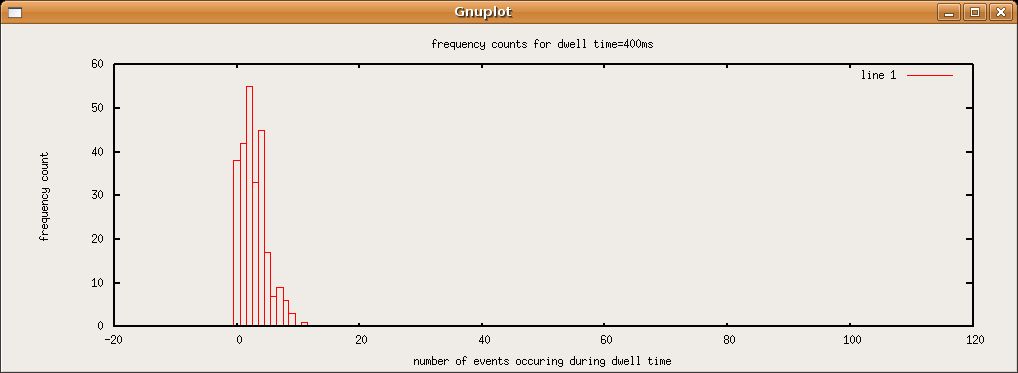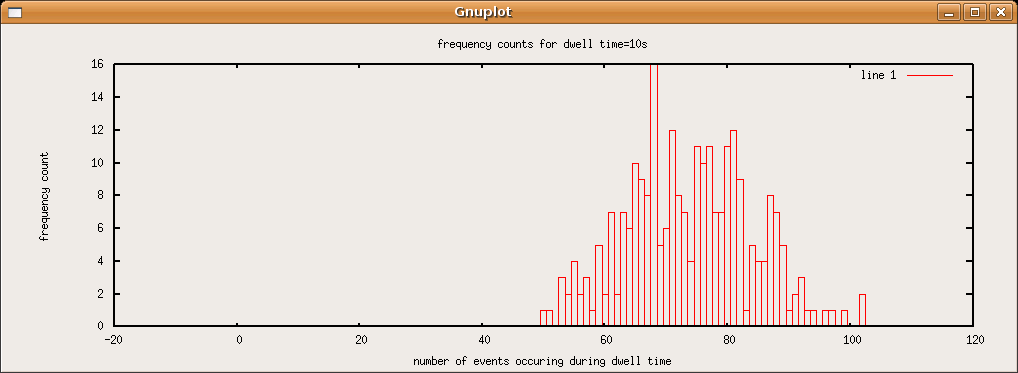
The plot that the script above produced with the data I obtained are shown in sequence below. As the dwell time increases, the most often occurring event count increases and the frequency vs. event count plots drift from something resembling a poisson distibution of a rarely occuring event to a the poisson distribution of a more common event, which resembles a gaussian.SJK 01:40, 22 October 2007 (CDT)

These graphs are very snazzy, and your data certainly are great...however, it's a bit tough to look at the data, because I don't have a way to "play" and "pause" the animated GIF. So, making the individual images available will definitely be necessary in your formal writeup.
I should point out that something interesting happened while we we counting events with a dwell of 200 ms. Our equipment recorded one instance where 27 events happened in that small dwell time. The mode of the data for dwell time=200ms was 0 events, and were were rarely getting counts more than or equal to 5.SJK 01:27, 22 October 2007 (CDT)

Very interesting! Bradley and Nik left the setup going from last Wednesday until today: 100 second bins, going like 5 days or something. I wonder if they will also record a similar occurance (though 27 events may not be obvious in a 100 second bin)?
By the way, you can easily calculate the probability of 27 events happening in a 200 ms window, given your Poisson fit. You can then use this probability to argue about throwing out that data point when fitting. (Also, you should directly state whether you throw the data out or not, and why.)
In Dr. Gold's lab manual, the poisson distribution is a model for the results of experiments that count random events that occur at a definite average rate and the frequency that one should expect to get a certain count number. If the expected average count is [math]\displaystyle{ \lambda }[/math], the probability that one will obtain the result of [math]\displaystyle{ k }[/math] after performing the counting experiment is
[math]\displaystyle{ f(k;\lambda)=\frac{\lambda^k e^{-\lambda}}{k!} }[/math]
So, to fit my data, I will have to normalize my data and find a suitable [math]\displaystyle{ \lambda }[/math] for each data set.
First off, normalize. If the frequency count of an event count [math]\displaystyle{ k }[/math] is [math]\displaystyle{ x_k }[/math], find some normalizing constant [math]\displaystyle{ N }[/math] so that [math]\displaystyle{ \sum_{k=\operatorname{min}\ k}^{\operatorname{max}\ k} \frac{x_k}{N}=1 }[/math]
Then, find [math]\displaystyle{ \lambda }[/math] such that[math]\displaystyle{ \sum_{k=\operatorname{min}\ k}^{\operatorname{max}\ k}\left(f(k,\lambda)-\frac{x_k}{N} \right)^2 }[/math] is a minimum
Duurrrrr... [math]\displaystyle{ N=256 }[/math] because 256 tests were performed each time.
SJK 01:38, 22 October 2007 (CDT)

It appears what you are doing here is a least squares fit of the Poisson distribution to the histogram, which is a great idea. However, I'd have to think some more, but I think maybe you would want a weighting factor in the denominator, perhaps [math]\displaystyle{ \sqrt{x_k} }[/math] (because the uncertainty in #counts is the sqrt(#counts)). Also, though, via talking with Bradley about this lab, I found that in the wikipedia article on Poisson distribution, they show that the maximum likelihood fit is when lambda is set to equal the average counts for the data. In your formal report, you should compare what you did with the much easier maximum likelihood method.
Through an iterative process, I determine [math]\displaystyle{ \lambda }[/math] to be 0.0261205 for dwell=10ms. Ack, I won't go any further, I'll just stop at 6 significant digits for the others too.
- 10ms,0.0261205
- 20ms,0.0736898
- 40ms,0.185892
- 80ms,0.457154
- 100ms,0.468385
- 200ms,0.937453
- 400ms,2.58578
- 800ms,5.74562
- 1s,7.27233
- 10s,73.9022
 SJK 01:44, 22 October 2007 (CDT)
SJK 01:44, 22 October 2007 (CDT)

From my glimpses of the moving GIFs, the fits do look good. In addition to being able to look at the individual images, the fits would probably also be easier to see if they were not also bars, but instead were data points, or curves...
how good are these fits, since I decided to stop at 6 sig figs (quite arbitrarily). I suppose I shall quantify this by taking the average of how far off the actual data is from the fit.
I think the formula is [math]\displaystyle{ Error=\frac{\sqrt{\sum_{k=\operatorname{min}\ k}^{\operatorname{max}\ k}\left(f(k,\lambda)-\frac{x_k}{N} \right)^2}}{\sqrt{N}\sqrt{N-1}} }[/math]
- 10ms, 0.0261205, 5.45905*10^-6
- 20ms, 0.0736898, 1.19310*10^-4
- 40ms, 0.185892, 3.28259*10^-4
- 80ms, 0.457154, 5.95464*10^-4
- 100ms, 0.468385, 3.15888*10^-4
- 200ms, 0.937453, 5.23153*10^-4
- 400ms, 2.58578, 5.22450*10^-4
- 800ms, 5.74562, 2.97039*10^-4
- 1s, 7.27233, 2.59775*10^-4
- 10s, 73.9022, 2.96150*10^-4
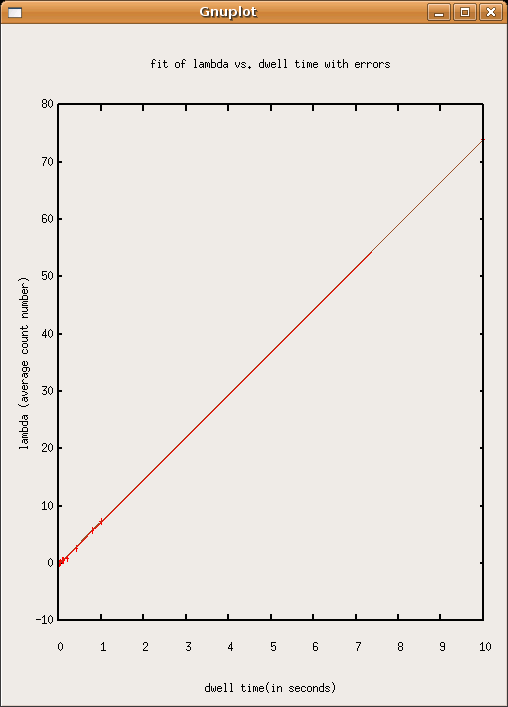
The poisson distribution fits count data of random events that happen at a definite average rate. Therefore [math]\displaystyle{ \frac{\lambda}{dwell time}=some constant }[/math]
A plot of [math]\displaystyle{ \lambda }[/math] vs. dwell time should fit on a line. to do this, I use Dr. Gold's linefit matlab function, modified for use with Octave. (www-hep.phys.unm.edu is down at the moment, maybe provide link when it comes back up or upload modded program here?) SJK 01:38, 22 October 2007 (CDT)

Really cool way to analyze your data (checking lambda versus window width to be linear)!
slope=7.39233+/-0.00003 intercept= -0.048099+/-0.000005 cov(m,b)=0.000000 correlation=0.999983 point error estimate=0.231612 chisq/ndf=265341
So, with our equipment set up the way it was (sorry, no data on this, oops!) we were observing events that occured at an average rate of 7.39 events per second.