Physics307L F07:People/Ritter/Formal lab report
Determining Planck's Constant Using the Spectra Produced By a Mercury Vapor Light Source
Brian Ritter (Britter@unm.edu)
UNM Dept. of Physics
November 5, 2007
Abstract
Planck's constant is one of the most important values in modern physics. In this experiment we look into the differences between the classical method of looking at light as well as the terms that brought scientists to develop the quantum model. The "Ultraviolet Catastrophe" of the classical theory of radiation predicted that the intensity of light emitted by a black body would increase to infinity as wavelength increased. Also, Wien's law was disproved by experiments. Maximum intensity of the light of a hot, glowing body disagreed from the prediction of the classical model. The solution to both of these problems is that the energy of a photon is based only on it's frequency, not it's intensity as classical thinking would have predicted. Along with this, Planck's constant is actually shown with the procedure I have used to be between the values of 5.92E-34(J*s) and 7.24E-34(J*s).
Introduction
This experiment has two important parts. Initially we look into the nature of light from both the classical and quantum models of light propagation. Classical theory would predict that as intensity dropped off, so would lights energy. Early experiments showed that this was in fact not true, and a photons energy would be instead based on the frequency. Experiment 1 is designed to further prove this fact.
Experiment 2 will build upon the findings of part one. The quantum model of light provides us with a formula that can be used to find the energy and well as the wavelength of a photon. This formulas is:
[math]\displaystyle{ E = hf = KE(max) + W }[/math]
This formula is used to describe what is known as the photoelectric effect. KE(max) is the maximum kinetic energy of emitted photoelectrons and W is the energy that would be needed to remove electrons from a surface. The h on the left hand side of this equality is known as Planck's constant. The purpose of part two of this experiment is to determine a value for this constant (1).
Methods and Materials
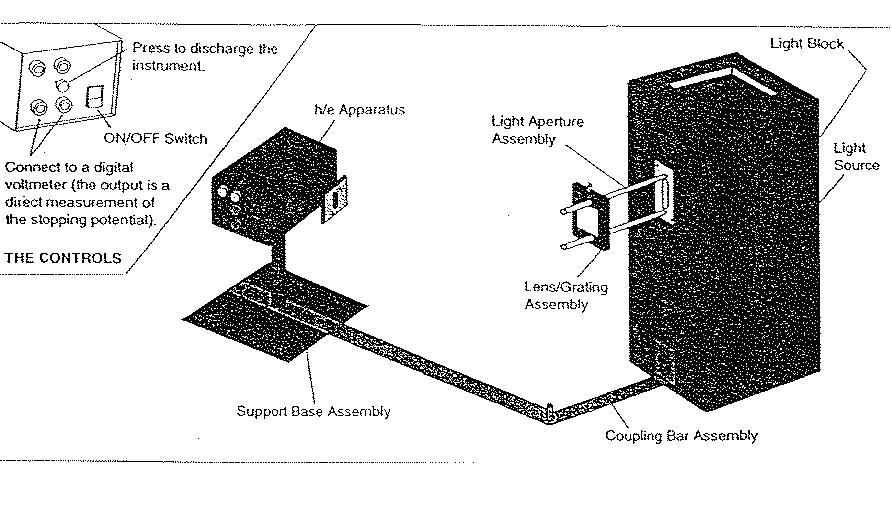
The experiment conducted is what is known as the h/e experiment. A mercury vapor light source is set up in front of an h/e apparatus. The light source produces a spectrum from the Hg vapor. This spectrum should emit light of yellow, green, blue, and violet wavelengths. Each individual spectral line is sent into the h/e apparatus which can then produce a voltage read on a digital voltmeter. These given voltages will be used to determine our value of h.
"Part I: Behavior of stopping voltage as light intensity is varied." The first step is to set up the equipment. A detailed procedure for setting up and using the equipment may be found at the manufacturer's web site. Connect your voltmeter to the output leads. Adjust the apparatus so that only one of the spectral colors falls upon the opening of the photodiode mask. In selecting the green or yellow line, it is important to use the corresponding filter. Place the variable transmission filter in front of the white reflective mask (and over the colored filter, if one is used) so that the light passes through the 100% section and onto the photodiode. Record the DVM reading. Press and release the instrument discharge button, and observe how much time is required to return to the recorded voltage. Move the variable transmission filter to the next section, record the new DVM reading, and the time to recharge after the discharge button has been pressed and released. I repeated all of these steps for all five sections of the filter. I would like to mention again to refer to the manufacturer's website. It was difficult initially to come up with the best way to measure the rise times accurately. In our first attempt, the voltmeter didn't seem to have the necessary precision for us to read. In our second attempt we tried to use an oscilloscope. this seemed without a doubt the most accurate route, but as it turned out, the rather long rise times proved the oscilloscope to be the wrong choice.
"Part II: Stopping Voltages of Different Frequencies of Light." Make sure focus and alignment are still ok. For each color in the first order measure and record the stopping potential (don’t forget the yellow and green filters). Repeat these five measurements to test for reproducibility. Move to the second order and repeat the above process, i.e. take two sets of readings
Results and Discussion
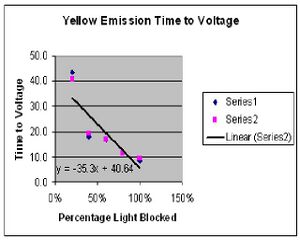
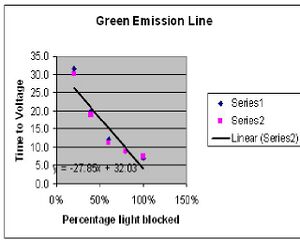
The results of experiment 1 were on course with what was expected. By placing the variable transmission filter in front of the our incoming light we were able to control the intensity of the given light. As expected, the output voltage read by our voltmeter stayed the same despite the intensity. All that changed was the time it took for the voltage to be reached. Fig. 1 and Fig. 2 show the results of the time versus intensity data collected. The predicted result would be a linear curve which is very close to what was achieved.
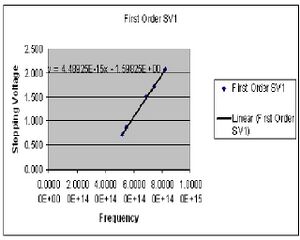
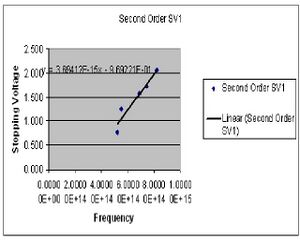
The results of experiment 2 are summarized in four least square charts (only 2 are given). The idea was to have four collected sets of data, two for the first order diffraction pattern and two for the second order. I have chosen to derive my value of h separately for the first and second orders because there seemed to be a measure of systematic error causing the numbers to fairly different. The desired value of h is reached by plotting the measured stopping voltage versus the known frequency of the visible light from the mercury vapor lamp. The slope of this curve gives the value of h/e. The value of h for the 1st order was found to be 7.2311E-34(J*s). This includes a standard deviation of 3.854E-36, and a standard error of +/-1.839E-36. For the second order I found h to be 5.944E-34(J*s) with a standard deviation of 2.601E-36 and a standard error of +/-2.724E-36.
Conclusion
The different values determined by the first and second order measurements were shown to be directly related to the filter used for the green light. The green filter used had little to no ability to block any of the higher frequencies of light. In looking at all of the original data taken it was very noticeable that all of the measured values were consistent with the exception of the green second order numbers. In returning to the lab it was found that the use of a simple glass was much more effective in blocking violet and ultra-violet light. It is then to be be concluded that the second order determination of the value of h is not correct for these reasons.