Physics307L F07:People/Mondragon/Notebook/071121

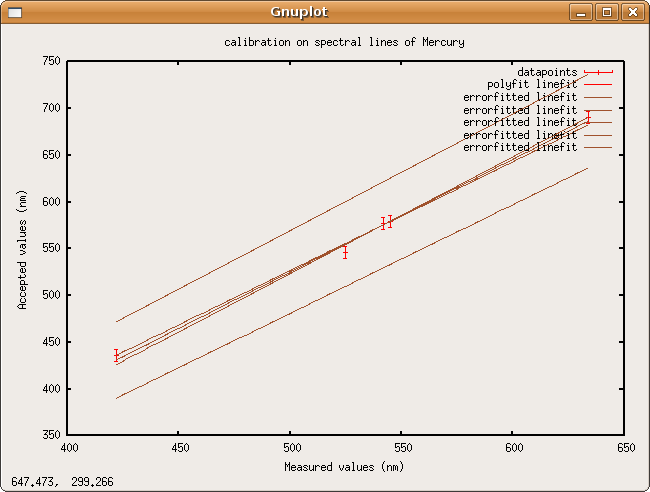
calibration

^{SJK 21:45, 1 December 2007 (CST)}

21:45, 1 December 2007 (CST)
You missed the fact that you were supposed to rotate the prism to correct for this mis-calibration! Your data would be much better in that case. (These methods may be appropriate after you've rotated the prism to the best of your abilities. (Also, did you account for the backlash?)

using mercury to calibrate. center of slit, measuring clockwise

calibration data

color	actual wavelength	measured wavelength
red	690.75nm	634nm
yellow	579nm	545nm
yellow	577nm	542nm
green	546.1nm	525nm
violet	435.8nm	422nm

so the calibration curve is [math]\displaystyle{ real\,wavelength=1.204205321\times measured\,value-76.8339591 }[/math]

the hydrogen spectrum

^{SJK 21:49, 1 December 2007 (CST)}

21:49, 1 December 2007 (CST)
Did you really only take one measurement for each color? (After calibrating correctly (above)), you need to take many "independent" measurements at each color to minimize uncertainty.

hydrogen spectum measurements and rough calculations

color	Measured Value	Actual Wavelength (nm)	Actual Wavelength (m)	1/wavelength	n	[math]\displaystyle{ 2^{-2}-n^{-2} }[/math]	Rydberg Constant
red	604	650.5060546	6.50506E-07	1537264.708	3	0.138888889	1.1068306E+07
blue green	466.5	484.927823	4.84928E-07	2062162.558	4	0.1875	1.0998200E+07
violet	421	430.1364809	4.30136E-07	2324843.496	5	0.21	1.1070683E+07
faint violet	400.2	405.0890102	4.05089E-07	2468593.259	6	0.222222222	1.1108670E+07

mean value for Rydberg constant=[math]\displaystyle{ 1.1061*10^{7}\,\mathrm{m}^{-1} }[/math] standard deviation [math]\displaystyle{ 4.6*10^{4}\,\mathrm{m}^{-1} }[/math]

CALCULATIONS

heres the excel file File:L and T Balmer series.xlsx Section above has numbers from the excel file.

here is a more careful analysis

Linefit says the calibration data fits the line [math]\displaystyle{ actual\,wavelength=(1.204205 \pm 0.042636)*measured\,wavelength-(76.833959 \pm 22.932003)nm }[/math]

Error propagation

No data on measurement error was ever taken, so, for any measurement of wavelength the error on the calculated actual value will be

[math]\displaystyle{ actual\,wavelength\,error=0.042636*measured\,wavelength+22.932003nm }[/math]

The calculated Rydberg constant is related to the measured wavelength value thusly
[math]\displaystyle{ \begin{align} \frac{1}{\lambda} &= R_\mathrm{H}\left(\frac{1}{2^2} - \frac{1}{n^2}\right), n=3,4,5,...\\ R_\mathrm{H} &= \frac{1}{\left(\frac{1}{2^2} - \frac{1}{n^2}\right)\lambda}\\ R_\mathrm{H} &= \frac{1}{\left(\frac{1}{2^2} - \frac{1}{n^2}\right)(m*\lambda_m+b)}\\ \end{align} }[/math]
Where [math]\displaystyle{ \lambda_m }[/math] is the wavelength measured by the instrument, [math]\displaystyle{ m }[/math] is the slope of the calibration curve, and [math]\displaystyle{ b }[/math] is the y intercept of the curve. Because of the uncertainty in the fit, the calculated value of the Rydberg constant will have uncertainty.

[math]\displaystyle{ \Delta R_\mathrm{H} = \frac{1}{\left(\frac{1}{2^2} - \frac{1}{n^2}\right)(m*\lambda_m+b)^2}(\Delta m*\lambda_m+\Delta b)= R_\mathrm{H} \frac{\Delta m*\lambda_m+\Delta b}{m*\lambda_m+b}=R_\mathrm{H} \frac{\Delta \lambda}{\lambda} }[/math]
The uncertiainty in R_H is just R_H times the relative uncertainty in the calculated wavelength.

hydrogen spectum measurements and rough calculations

color	n	Accepted Wavelength (nm)	Measured Value	Calulated Actual Wavelength (nm)	Calculated Error(nm)	Relative Error	Actual Wavelength (m)	Rydberg Constant	Rydberg uncertainty
red	3	656	604	650.506	48.684	0.074840	6.50506E-07	1.10683E+07	8.284E+05
blue green	4	486	466.5	484.928	44.822	0.088305	4.84928E-07	1.09982E+07	9.712E+05
violet	5	434	421	430.136	40.882	0.095044	4.30136E-07	1.10707E+07	1.0522E+06
faint violet	6	410	400.2	405.089	39.994	0.098731	4.05089E-07	1.11087E+07	1.0968E+06

Average for Rydberg constant= [math]\displaystyle{ 1.10592*10^7\,\mathrm{m}^{-1} }[/math]. Uncertainty of average = [math]\displaystyle{ 9.64*10^5\,\mathrm{m}^{-1} }[/math]. Accepted value = [math]\displaystyle{ 10 967 758.341 \pm 0.001\,\mathrm{m}^{-1} }[/math]