Physics307L F07:People/Martin/Notebook/070926
Planck's Constant
Link to Lab partners page Physics307L F07:People/Smith/Notebook/3
Equipment
SJK 03:37, 11 October 2007 (CDT)

recording model numbers is great!...can you do it for all the instruments (including voltmeter)?
- Mercury Vapor Light Source from Pasco scientific OS-9286, 115 volts
- h/e apparatus from Pasco scientific AP-9638
- A relative transmission (changes the intensity of the incident light)
- A digital voltmeter
Setup
The mercury light emitter and the h/e apparatus are already connected by a coupling bar assembly. All we need to do is to connect our digital multimeter to the output plug ins on the back of the h/e apparatus.
Purpose
The purpose of our experiment is to determine the value of plank's constant (h). We will do this by examining the photoelectric effect and using the equation [math]\displaystyle{ E=hf=KE+W }[/math] where f is the frequency of the incident light, W is the work function (amount of energy required to eject an electron from the metal plate, h is plank's constant and KE is the max allowed kinetic energy for the ejected electrons.
Measurements
- note we are measuring the stopping potential for light of a given frequency. The stopping potential is the potential that is required to stop electrons from jumping and creating a current. Measuring this gives us a linear relationship between f and this stopping potential.
Values for wavelengths of light we are using
- Yellow- 578 nm
- Green- 546.074 nm
- Blue- 435.835 nm
- Violet- 404.656 nm
- UV- 365.483 nm
Values above in frequency
- Yellow- 5.18672E14
- Green- 5.48996E14
- Blue- 6.87858E14
- Violet- 7.40858E14
- UV- 8.20264E14
Experiment 1
Part A
Experiment 1 results using yellow light and the green light
| Yellow Line, Filtered | ||||||
|---|---|---|---|---|---|---|
| Time Required to return to recorded voltage (seconds) | ||||||
| Transmission % | Stopping Voltage | Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 |
| 100 | 0.74V | 3.08 | 3.63 | 3.29 | 2.19 | 3.28 |
| 80 | 0.74V | 2.42 | 3.22 | 3.24 | 2.75 | 2.89 |
| 60 | 0.74V | 2.87 | 5.00 | 4.43 | 3.74 | 3.90 |
| 40 | 0.74V | 6.66 | 6.30 | 8.43 | 6.58 | 6.96 |
| 20 | 0.74V | 10.69 | 11.69 | 11.29 | 10.39 | 12.77 |
| Green line, Filtered | ||||||
|---|---|---|---|---|---|---|
| Time Required to return to recorded voltage (seconds) | ||||||
| Transmission % | Stopping Voltage | Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 |
| 100 | 0.87V | 8.17 | 8.25 | 8.76 | 9.09 | 7.33 |
| 80 | 0.87V | 8.03 | 8.19 | 7.43 | 6.97 | 8.1 |
| 60 | 0.87V | 15.2 | 11.53 | 12.05 | 12.03 | 12.37 |
| 40 | 0.87V | 20.32 | 18.93 | 17.72 | 15.66 | 17.13 |
| 20 | 0.87V | 23.29 | 30.30 | 31.17 | 31.05 | 31.79 |
Part B
| Color | Voltage |
|---|---|
| Yellow | 0.75 V |
| Green | 0.87 V |
| Blue | 1.50 V |
| Violet | 1.70 V |
| UV | 2.05 V |
Experiment 2
Determining h, light frequency and the stopping voltage are directly proportional and the proportionality constant is h (The slope)
| Order 1 | Order 2 | |||
|---|---|---|---|---|
| Color | Stopping Voltage 1 | Stopping Voltage 2 | Stopping Voltage 1 | Stopping Voltage 2 |
| yellow | 0.76V | 0.75V | 0.71V | 0.71V |
| Green | 0.88V | 0.87V | 0.88V | 0.87V |
| Blue | 1.52V | 1.5V | 1.58V | 1.58V |
| Violet | 1.74V | 1.7V | 1.74V | 1.75V |
| UV | 2.07V | 2.05V | 2.06V | 2.1V |
- note we had to adjust the focus on the second order yellow and green lines to get a reasonable number for the stopping voltage.
Analysis
Note whene calculating the value of h the equation [math]\displaystyle{ KE=hv-W }[/math] or the stopping potential which is [math]\displaystyle{ Vstop=(1/e)(hv-W) }[/math]
These are the graphs for our mean times to return to our initial measured voltages v %of light transmitted
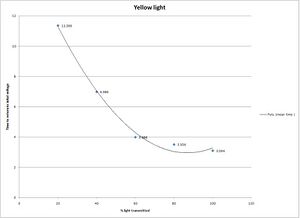
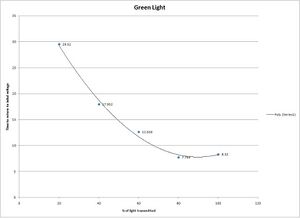
Why does the time to return to the original voltage reading increase as we decrease the % of transmitted light and therefore decrease the intensity?
SJK 03:25, 11 October 2007 (CDT)

Good answer!
The intensity of light effects how many electrons are displaced during the photoelectric effect not the energy that they have after displacement. Since the h/e appratus that we used the buildup of electrons to create its stopping potential the less intense the light, the less electrons displaced, the slower the buildup of the stopping potential (the voltmeter readout).
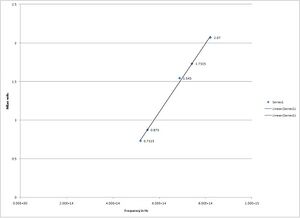
This is my graph for the frequency v stopping potential
SJK 03:28, 11 October 2007 (CDT)

Great job reporting the uncertainty! This would be easier to read if you used same exponent for value and uncertainty. And also, fewer digits. e.g.:
(7.2 +/- 0.2) E-34 J s
Our result for h was- 7.17E-34 Js +/- 2.31E-35 Js
Our result for W was- 2.15E-19 J +/- 2.3E-20 J
with the true value of h being 6.63E-34 we had a percent error of 8.14% we could have better results but having less then ten percent error is fairly good.
This data supports the idea of a quantum description of light, one where the stopping potential depends on the frequency rather then the intensity