Physics307L F07:People/Le/Formal2
Discovering the Fundamental Charge and Investigating Quantized Amounts of Charge Using the Milikan Oil Drop Experiment
Linh Le, Cary Dougherty
Physics and Astronomy Department, Junior Lab 307, University of New Mexico, Albuquerque, New Mexico
Email: linhle@unm.edu
Abstract
To explain the connection between electricity and matter, scientists in the late 19th century argued there had to be a fundamental unit of electricity. To find this fundamental unit, we repeated Robert Millikan's famous Oil-Drop Experiment. The Millikan Oil drop experiment is the product of other attempts. The Millikan experiment was best at determining the charge of an electron, and showing the quantized nature of these charges.
To repeat Millikan we sprayed oil droplets into a capacitor and then ionized the droplets to give them excess electrons. We then exposed these droplets to a constant electric field. Measuring the fall time of the droplets without the field, then measuring the rise time with the field on, we were able to compare the force of gravity pulling down on the droplets to the force of the electric field causing them to rise. In doing so, we were able to get a fundamental charge of [math]\displaystyle{ (1.558+/-0.026) x 10^{-19} coulombs }[/math], very close to the accepted value of [math]\displaystyle{ 1.60217733x10^{-19} }[/math] Coulombs.
Introduction
SJK 00:22, 7 December 2007 (CST)

This is a good start on the introduction. Here's how to finish it: It starts out great, and if you can cite references to famous research papers. I know you can do this for Millikan (I've found it myself), not sure about Thompson. You end first paragraph by saying what technique Millikan used...continue by saying what his main conclusion was. Then add a bit about other ways the electric charge can be measured, cite some original research papers. Say what method is used to determine the currently accepted value. D. Loomba (UNM P&A) et al. published a paper last month of a very cool automated version of the Millikan oil drop experiment. So, those are some things to add. After this would be a good point to go into what you are doing in this paper. Right now your ending sentence is vague and doesn't lead into the rest of the paper. You could even end with a similar sentence to the "We are recreating..."
Late in the 19th century, JJ Thompson discovered that the beam of light in a cathode ray were attracted by positive charges and deflected by negative charges. This helped discover that this beam was electrons, and that they were smaller than a hydrogen atom.(1) Later, Thompson experimented with ionized water in electric fields, but water tends to be flimsy and using acid to find the charges on the water was tricky. Robert A Millikan improved on JJ's experiment by using oil droplets. Oil droplets are sturdier than water. Millikan then used the electric field to balance the force of gravity on the droplets with the upward pull of the electric field on the charges. (2)
We are recreating Millikan's famous experiment looking for the fundamental charge of the electron and whether or not the electron's charge is quantized. The e/m ratio had been known for a long time, but with after this experiment, the charge and the mass of the electron finally had a number. A second consequence was the discovery of quantized charge. The observation of decay had sparked it, but now there is more evidence supporting a quantum nature of particles.
Methods and Materials

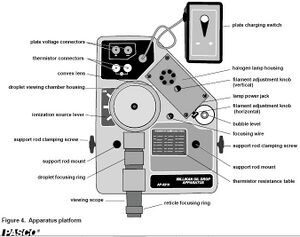
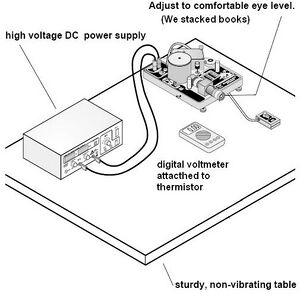
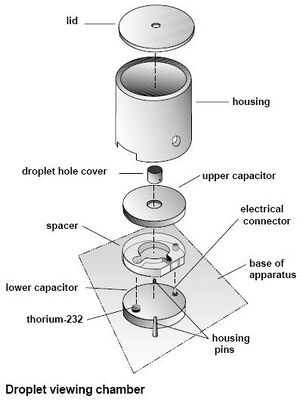
- "Millikan Oil Drop Apparatus" by PASCO Scientific Model AP-8210.Manual
- Tel-Atomic 50V & 500V supply
- Fluke 111 True RMS Multimeter
- Squibb's Mineral Oil
- Smiec 0-25mm 0.01mm Micrometer
- Steve Koch 00:37, 7 December 2007 (CST):It is better to work these into the text, than list them. For example, "We connected the power supply (Tel-Atomic 500V)..." and "...filled the oil spray bottle with mineral oil (Squibb's Mineral Oil)."
Procedure
Setup
The apparatus did not require any extra assembly to operate. We connected a power supply to the capacitor leads, a digital multimeter to the thermistor, plugged the light source into a wall socket, and filled the oil spray bottle with the mineral oil. After raising the apparatus to a comfortable eye level (books were used) we adjust it to be level using the built in leveling gauge and the adjustable feet. (See Fig 4)
To calibrate the apparatus, we opened up the cylindrical housing for the capacitor and took out the droplet hole cover, the upper capacitor plate and the spacer. After measuring the spacer with a micrometer, we replaced it and the upper plate. Unscrewing the focusing wire (located to the right of the capacitor) we placed the wire through the hole in the top of the upper plate and replaced everything else but the droplet hole cover. With the room dark and the lamp plugged in, we looked through the microscope and put the needle in focus, adjusting the amount of light entering the capacitor as appropriate. With the needle and grid inside the eyepiece all focused, we opened the housing, removed the needle, and replaced the droplet hole cover. (See Fig 5)
Experiment
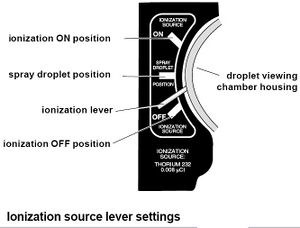
After the apparatus has been setup, we begin by introducing the oil to the capacitor. We placed the special nozzle of the oil sprayer into a small hole in the top of the lid. To the right of the housing is a lever,(see fig 6) the lever must be set to the middle position "Spray Droplet" to allow the oil to enter the capacitor. While someone is watching the microscope, a quick spray followed by smaller, slower sprays are applied (it is helpful to remove the nozzle from the hole before releasing the sprayer to prevent the air from being sucked back out of the capacitor). The oil droplets will appear to be a "shower of sparkles" as the fall into view. Continue spraying until you see a fair amount of particles in view.
After the oil is inside the chamber, we remove the nozzle and set the lever down to the "off" position. We then switch the lever to the "on" position for 2 or 3 seconds to allow the ionizer to ionize the oil particles, then switch it back to the "off" position. To check that the oil droplets are properly ionized, we looked through the microscope and switched the polarity of the plates (see fig 3) to see if the oil droplets react differently. Ideally, they should rise when the upper plate is polarized positive (+) and fall faster when the it is polarized negative (-).
After the droplets have been properly ionized, we sought out to isolate a single droplet of which to study. The droplets can be separated by moving them by switching the polarities in the plates. Using the grid within the eyepiece of the microscope, we looked for a droplet that fell .5mm (one large unit in the grid, or 5 smaller units) in 15 seconds and rose the same amount in 3 seconds. Once a particle of that nature was found, we recorded its fall time and rise times 10 times each(when possible). After taking sufficient data, we turned the ionizer back to the "on" position for 1 or 2 seconds and repeated the experiment with the same droplet (when possible).
Data Analysis
SJK 00:29, 7 December 2007 (CST)

You should say what software and algorithms you use to do these calculations. Also, describe the method for deducing the fundamental charge value (and cite if anyone helped you develop it).
Using the fall and rise times, we were able to determine a few things about the droplets and the charge.
To find the fall and rise times, we said that [math]\displaystyle{ V=\frac{d}{t} }[/math]. We use this simple formula since the droplets reach terminal velocity very quickly and travel at a constant rate after that.
To find the charge stored in the electron:
[math]\displaystyle{ q = {\frac{4}{3}}\pi \rho g[\sqrt{(\frac{b}{2p})^2 +\frac{9 \eta v_f}{2g\rho}}-\frac{b}{2p}]^3\frac{v_f + v_r}{Ev_f} }[/math]
A nice detailed derivation of this formula can be found in the manual, linked above.
q- the charge of the electron
p-barometric pressure-[math]\displaystyle{ 8.33^4Pa }[/math]
d-distance between capacitor plates
g- acceleration due to gravity- [math]\displaystyle{ 9.8 \frac{m}{s^2} }[/math]
b- constant [math]\displaystyle{ 8.20E(-3)Pa * m }[/math]
a- radius in drop measured in meters
[math]\displaystyle{ \rho }[/math]-density of the oil which is [math]\displaystyle{ 886 \frac{kg}{m^3} }[/math]
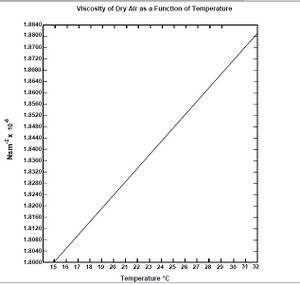
[math]\displaystyle{ \eta }[/math]- viscosity of air (found by the comparing temp inside the capacitor see figs 7,8)
V- potential difference across the plates in Volts
[math]\displaystyle{ v_r }[/math]- rise velocity (dividing .5mm by rise time)
[math]\displaystyle{ v_f }[/math]- falling velocity (dividing .5mm by rise time)
E electric field (found by [math]\displaystyle{ \frac{V}{d}) }[/math]
Results
Raw Data
Due to the length of the raw data, it will be included at the end of the paper in an appendix
Calculated Data
| Trial | E field (V/m) | Viscoscity of Air e-5(Ns/m^2) | Vfall Avg e-5(m/s) | Vrise Avg e-5(m/s) | Q e-19 (couloumbs) |
|---|---|---|---|---|---|
| 1A | 61851.85 | 1.848 | 3.408 | 1.205 | 3.39 |
| 1B | 61886.56 | 1.848 | 3.608 | 2.118 | 6.38 |
| 2 | 61652.28 | 1.852 | 3.225 | 1.683 | 4.84 |
| 3 | 61775.59 | 1.844 | 2.855 | 1.106 | 3.08 |
| 4 | 61901.59 | 1.852 | 3.243 | 2.304 | 6.34 |
There is a noticeable trend in rise times vs the number we got for Q. Plotting them below, we can see that some values tend to group together. This leads me to believe the quantized nature of the charges. http://openwetware.org/images/a/ae/Qvsrise.JPG
Taking notice of this, I averaged the values that were close, and set the lowest value as 1Q, 2nd highest as 2Q, etc. Using a least squares fit, I found the value for the fundamental charge to be [math]\displaystyle{ (1.5575+/-0.00046725)x 10^{-19} coulombs }[/math] http://openwetware.org/images/8/8c/Milikan_Q.JPG
Conclusion
SJK 00:34, 7 December 2007 (CST)

Conclusions and "Sources of error" is still way too informal. COnclusion should be brief, mentioning what you have found and what could be done next (which possibly may be addressing the likeliest source of largest error). Other sources of error can be mentioned earlier when it is relevant. For example, in Methods, you can state the air pressure you are using, and how much that may vary and why or why not it is significant.
The experiment went very well, with no huge sources of conflict. Since the actual value of the fundamental charge is known, our value can be compared to it for a qualitative accuracy of the experiment.
[math]\displaystyle{ %error= \frac{|Actual-Experimental|}{|Actual|}x100 }[/math]
[math]\displaystyle{ %error= \frac{|1.60217646 x 10^{-19}-1.5575 x 10^{-19}|}{|1.60217646 x 10^{-19}|}x100 }[/math]
[math]\displaystyle{ %error=2.78 }[/math]
Sources of Error
There is plenty of room for error in this lab.
- I went on the internet to find the atmospheric pressure in Albuquerque, but that is probably an estimated quantity and changes with specific altitude of your area and the weather at the time
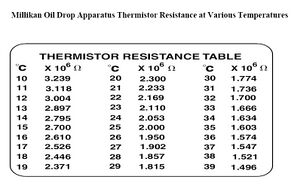
- The viscosity of the air inside the capacitor is measured by the temperature inside the capacitor. That value is determined by measuring the resistance in a thermistor and then finding values on a chart.
- The temperature is estimated off a chart, but when you get a value for the resistance that falls between values, you have to round
- Once the temperature is found, you look at a graph to find the value, and as above, you have to round
- While measuring the fall and rise times of the droplets, it is uncertain how close or far the droplets are, so adjusting the microscope might change the distance that they travel (although it is assumed the apparatus is calibrated to prevent this)
- There is also "lag time" between measurements as one of us stared into the scope and the other was running the stopwatch
- There is substantial Brownian Motion in the droplets that maybe skew the fall and rise rates
- The major partition lines on the grid in the eyepiece are just as wide as the droplet themselves, so knowing when to start and stop the clock is a little ambiguous.
- The voltage read off our supply seems to increase with time (systematic error) this effects the electric field causing the droplets to rise faster.
Acknowledgments
I would like to thank the following people:
- My lab partner Cary Dougherty, for helping take measurements
- The lab professor, Dr. Koch, for getting this all working
- Kyle Martin and Jesse Smith, from whom I borrowed my charge calculation method from
- Millikan, for discovering this in the first place
References
Determination of the Charge on an Electron 2
Appendix 1
Spacing of plates: 8.10mm
Density of Squibb's Mineral Oil: 886kg/m^3
Atmospheric Pressure in Abq (as looked up on the internet): 8.33X10^4 Pa
Set 1
Voltage: 501V Resistance: 1.9982 M(ohms) Distance: .5mm
| Fall Time (s) | Rise Time (s) |
|---|---|
| 18.38 | 3.31 |
| 14.38 | 3.15 |
| 14.11 | 5.14 |
| 13.7 | 5.7 |
| 13.8 | 5.19 |
| 14.72 | 5.52 |
| 14.5 | 5.23 |
| 13.13 | 5.27 |
| 15.37 | 5.37 |
| Avg Fall Time | Avg Rise Time |
| 14.67s | 4.877s |
In this set, we were able to change the charge on the droplet and remeasure
Voltage=501.9V Resistance=1.976M(ohms)
| Fall Time (s) | Rise Time (s) |
|---|---|
| 13.28 | |
| 13.86 | 2.19 |
| 14.58 | 2.21 |
| 13.09 | 2.70 |
| 14.38 | 2.46 |
| 13.94 | 2.24 |
| Avg Fall Time(s) | Avg Rise Time(s) |
| 13.855 | 2.36 |
Set 2
Voltage: 500V Resistance: 1.923M(ohms)
| Fall Time(s) | Rise Time(s) |
|---|---|
| 15.97 | 2.99 |
| 14.50 | 3.13 |
| 13.80 | 2.95 |
| 15.50 | 2.69 |
| 15.17 | 2.75 |
| 15.36 | 3.36 |
| Avg Fall Time(s) | Avg Rise Time(s) |
| 15.05 | 2.97 |
We changed the charge of the oil droplet in this set as well, but the droplet moved so fast, that it was very hard to sync Cary's observations and oral commands with my data collecting. As that is the case, we only took 2 data points.
| Fall Time (s) | Rise Time(s) |
|---|---|
| 9.70 | .72 |
| 10.32 | .73 |
Set 3
Starting Voltage: 501.0 V Resistance: 2.07 M(ohms) Ending Voltage:501.8 V 2.041M(Ohms)
| FALL TIME (s) | RISE TIME (s) |
|---|---|
| 14.87 | 4.81 |
| 17.53 | 4.87 |
| 17.17 | 4.85 |
| 18.67 | 4.57 |
| 17.89 | 4.53 |
| 17.77 | 4.37 |
| 15.93 | 4.56 |
| 16.49 | 4.90 |
| 18.97 | 4.61 |
| 18.41 | 5.11 |
| 19.24 | 2.50 |
| Avg Fall Time(s) | Avg Rise Time(s) |
| 17.54 | 4.52 |
Set 4
Starting Voltage:501.4 V Resistance:1.945 M(Ohms)
| Fall Time (s) | Rise Time (s) |
|---|---|
| 16.13 | 2.23 |
| 14.29 | 2.14 |
| 14.85 | 2.47 |
| 15.96 | 1.93 |
| 16.49 | 1.99 |
| 14.79 | 2.25 |
| Avg Fall Time(s) | Avg Rise Time(s) |
| 15.42 | 2.17 |