Physics307L F07:People/Gooden/Formal Lab Report II
- MEASURING THE SPEED OF LIGHT BY A TIME DELAYED SIGNAL BETWEEN A LIGHT EMITTING DIODE AND PHOTOMULTIPLIER TUBE
Author: Matthew E. Gooden
Experimentalists: Matthew E. Gooden, Zane Gibson
Department of Physics and Astronomy
University of New Mexico
Albuquerque, NM
1. Abstract
The Speed of Light, often denoted by c is one of the most important physical constants in physics, being a basis for special relativity, and appearing in almost all branches of physics. This experiment was done to determine the value of the speed of light. Using a time amplitude converter and an oscilloscope to measure the time between the emission of a light signal by a light emitting diode and the detection of the light signal by a photomultiplier tube. By varying the distance between the LED and PMT we were able to record different times using the above mentioned equipment. Recording the changes in distance between the PMT and LED and the time for the signal we then plotted distance vs. time and using a linear least-squares fit found the speed of light from the slope of the line. From this experiment we have measured the speed of light to be [math]\displaystyle{ c=\left(2.892 \pm .077\right)\times10^8 m/s }[/math] in fair agreement with the accepted value of [math]\displaystyle{ 2.99\times10^8 {m/s} }[/math].
2. Introduction
This experiment investigates the speed of light. The speed of light is how fast light travels,but the value of c also represents how fast any electromagnetic wave/photon(due to wave particle duality) travels in vacuum. The speed of light historically have been very fascinating. Since the time of Aristotle it was believed that light travels instantaneously between locations, that its speed was infinite. However, once physicists began investigating more and they discovered that the speed of light is very large, but a finite value and specifically it is around 300 million meters per second by todays calculations. In the 19th century with James Clark Maxwell and his equations for electromagnetism[1] it was discovered that all electromagnetic phenomena travel at that same speed, and specifically from his equations was defined as [math]\displaystyle{ c=\frac{1}{\sqrt{\epsilon_o \mu_o}} }[/math] where the two constants are the permittivity of free space and permiability of free space respectively. Physicists also believed that light followed Galilean relativity/motion and that its speed was always dependent upon the reference frame from which it was measured. However, Albert Einstein showed in 1905 with his paper "On the Electrodynamics of Moving Bodies" [2] that the speed of light is a constant, that it is independent of the reference frame from which it is measured. In the 1940's to 1950's other scientists attempted to measure the speed of light and most notably was Louis Essen, who in 1946, measured the speed of light using a microwave cavity, of very precisely known dimensions. Essen measured the normal modes of the cavity and since for each normal mode only certain frequencies and wavelength are allowed he used the equation [math]\displaystyle{ c=\lambda \nu }[/math] to find the speed of light[3]. .Essen's background was in time-measurement and so measuring the speed of light precisely would allow for very accurate time measurements, and today the second is even defined to be the time it takes light to travel [math]\displaystyle{ \left ( \frac{1}{2.99} \right )\times10^ -8 }[/math] meters[4]. In this paper we used a Time Amplitude Converter along with an oscilloscope to measure the time delay between a signal from a Light Emitting Diode and a Photomultiplier tube to measure the speed of light, which we have measured to be [math]\displaystyle{ c=\left(2.892 \pm .077\right)\times10^8 m/s }[/math] and compared with the accepted value of [math]\displaystyle{ c=2.99\times10^8 m/s }[/math] it is in good agreement.
3. Methods and Materials
Equipment List:
1.Time-Amplitude Converter (TAC) - EG&G Ortec Model 567 TAC/SCA
2.Light Emitting Diode
3.Photomultiplier Tube (PMT) - Magnetic Shield Co., 22P50
4.DC Power supply (LED) - Harrison Laboratories, Model 6207A 0-160V,0-.2A
5.DC Power supply (PMT)- Bertan Associates,Inc. Model 315, DC Power Supply 0-5000V,0-5mA
6.Oscilloscope - Tektronix TDS 1002 2 Channel Digital Storage Oscill., 60MHz 1GS/s
7.Delay box - Canberra NSEC Delay Box, Model 2058
8.Several Meter Sticks - 4
9.Long Tube (cardboard or other nontransparent material) - 4 meters long
Procedure:
- Equipment Set up:
In this section I want to describe how we set up the equipment, in the way that allowed us to begin the experiment and collect data.During the set up of the equipment listed above, and during the coarse of the experiment that the PMT was never exposed to direct light while its power supply was connected and turned on, because the direct light will cause such a current flow through the PMT that it destroyes the circuitry. We first began to set up the equipment by connecting a meter stick to the LED and then fastening several meter sticks together. Then we connected the power supplies for the PMT and the LED (items 5 and 4 above respectively), while not turning the power supplies on to avoid damaging the PMT. Then we inserted the PMT and LED into opposite ends to the tube, keeping the PMT on the side nearest the equipment and where we were positioned. We picked an arbitrary point to call our zero or begining point on the meter sticks from which to base measurements. Then we connected the LED to the TAC's start jack with a BNC cable, and also connected the PMT to the stop jack on the TAC with another BNC cable. Next we ran a cable from the PMT to the oscilloscope's Channel 1 and from the TAC to channel 2 on the oscilloscope.The oscilloscope was used measure the voltage output from the PMT on channel 1 and the signal from the TAC that respresented the time delay that we wanted to measure.
- Configuration and Data Collection:
Here I would like to describe how we configured the equipment and performed the data collection for this experiment. After completing the set up mentioned above, we turned on all the equipment and began adjustments. We left the delay box set to zero delay for the experiment, as none was ever needed. We then adjusted the voltage knob on the PMT power source(Photo 1, Figure 1 below) so that the PMT was receiving a voltage of approximately 1900 volts. Then we adjusted the LED power supply to approximately 200 volts(photo 2, Figure 1). Then turning to the oscilloscope we saw two signals present on the screen, one from the PMT and the other from the TAC. The PMT signal was charcterized by a sharp downward voltage drop, while the TAC signal was characterized by a rapidly oscillating square wave. Using the aquire button on the oscilloscope we chose to average over the values that the oscilloscope is recieving to allow measurments to be taken must easier. We chose the 128 setting under the average command, to greatly stabilize the signal we were viewing. At this point we began our data collection, having one of us at the other end of the tube to move the LED, and the other at the end with the PMT and other equipment. We picked a value of the voltage on Ch 1 and attempted to maintain that value for the duration of the measurments made for each data set, this is need because as the LED is moved toward or away from the PMT the intensity of the signal changes and by alligning or unalligning the polarizers we were able to keep the signal constant. This was accomplished by turning the PMT left/right to allign or unallign its polarizer with that of the LED. Taking care to note our chosen zero mark, we then moved the LED away from the PMT a short distance, recording this change in distance, while holding the PMT steady. For this experiment, we are not concerned with the actual distance between the PMT and LED. Rather at any particular distance between the PMT and LED we make a measurment and then we are only concerned with the change in that distance for the next measurment, since we are measuring the time delay of the signal from the LED pulse and the PMT signal. Once the LED was moved the PMT was adjusted to regain the chosen voltage, and then using the measure function to allow us to see the values outputed to channels 1 and 2, we recorded the voltage output from the TAC. To complete the particular data set we made several more measurements in the same fashion always recording the change in distance from the original zero mark. For future data sets we made different choices in the chosen PMT voltage, and the distances that we recorded at.
- Figure 1
-
Photo 1:Center is a storage rack for several pieces of equip. From left: power supply for photomultiplier-Item 5, delay box-Item 7, TAC (time amplitude converter)-Item 1
-
Photo 2:Small gray box center of the photo is the Power supply used for LED light emitter. Item 4 from equip. list
-
Photo 3:Oscilloscope. Item 6.
-
Photo 4:On top tried different time delay to try and get better signal.
- Data Analysis:
Analysis of the data collected from this experiment was done using several software packages: Excell and Matlab. The data was placed into Microsoft Excell were we performed linear least-squares fits to each data set. We fit the data keeping Distance vs. Time in mind, by considering the recorded distances to represent our y-values and the times as our x-values. Then using Excell's built in Least-squares algorithms, which run off of following, where the x and y are as described above:
- [math]\displaystyle{ S_X = x_1 + x_2 + \cdots + x_n \, }[/math]
- [math]\displaystyle{ S_Y = y_1 + y_2 + \cdots + y_n \, }[/math]
- [math]\displaystyle{ S_{XX} = x_1^2 + x_2^2 + \cdots + x_n^2 \, }[/math]
- [math]\displaystyle{ S_{XY} = x_1 y_1 + x_2 y_2 + \cdots + x_n y_n. \, }[/math]
Slope: [math]\displaystyle{ m = {n S_{XY} - S_X S_Y \over n S_{XX} - S_X S_X}. \, }[/math]
Intercept: [math]\displaystyle{ b = {S_Y - m S_X \over n}. \, }[/math]
Once we obtained the Linear Least-squares parameters m and b we then went to Matlab where we used the two parameters to create an inline function. Then by selecting a range of times to plot over, we were able to plot the least-squares fit line and then add on our data on top of the fit(see figure 2, below in Reslts/Discuss). Although using the functions above, the least-squares fit could have been done also with Matlab we chose to rely on Excell to produce the parameters m and b rather than code in the functions into Matlab. Along with the Least-squares analysis we performed on the data, we used a weighted average of the reported speed of light for each data set to obtain a final reportable value for this paper. To perform the weighted average we used
- [math]\displaystyle{ w_i = \frac{1}{\sigma_i^2}. }[/math]
The weighted mean in this case is:
- [math]\displaystyle{ \bar{x} = \frac{ \sum_{i=1}^n x_i/{\sigma_i}^2}{\sum_{i=1}^n 1/{\sigma_i}^2}, =\frac{ \sum_{i=1}^n x_i {w_i}}{\sum_{i=1}^n {w_i}}, }[/math]
and the variance of the weighted mean is:
- [math]\displaystyle{ \sigma_{\bar{x}}^2 = \frac{ 1 }{\sum_{i=1}^n 1/{\sigma_i}^2}, }[/math]
which reduces to [math]\displaystyle{ \sigma_{\bar{x}}^2 = \frac{ {\sigma_0}^2 }{n} }[/math], when all [math]\displaystyle{ \sigma_i = \sigma_0\, }[/math].
Where the [math]\displaystyle{ \sigma 's }[/math] are the found standard deviations for each value of c from each data set. More information of the weighted average can be found in the references [5].
4. Results and Discussion
Data: In this section I will present the three data sets that were taken in the course of this experiment, and give the approximate speed of light c obtained from that data set. Also a fourth data set to be analyzed seperately. Then I will describe what took place during each set and any ideas we have on the cause of error in the reported value for that data set.
- In analyzing the data we used the equation :[math]\displaystyle{ V = G*T }[/math] to relate the voltages to time, with G=1/10 volts/nanosecond
- Table 1:Each row represents a seperate measurement that was made. Column 2 is the PMT voltage chosen to be constant throughout the data set. Column 3 represents the Voltage measured on the Oscilloscope being recieved from the TAC. Column 4 is the recorded change in distance between PMT and LED. Column 5 is the associated time with the voltage output of the TAC.
| Data Set 1 Measurments | PMT Ch1 Voltage | TAC Time delay voltage | Distance (cm) | Time (ns) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.24\pm.04 }[/math] | 60 | 32.4 |
| 2 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.2 \pm.04 }[/math] | 80 | 32 |
| 3 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.08 \pm.04 }[/math] | 100 | 30.8 |
| 4 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.00 \pm.04 }[/math] | 120 | 30 |
| 5 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.96\pm.04 }[/math] | 140 | 29.6 |
| 6 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.00 \pm.04 }[/math] | 130 | 30 |
| 7 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.12 \pm.04 }[/math] | 90 | 31.2 |
| 8 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.2 \pm.04 }[/math] | 70 | 32 |
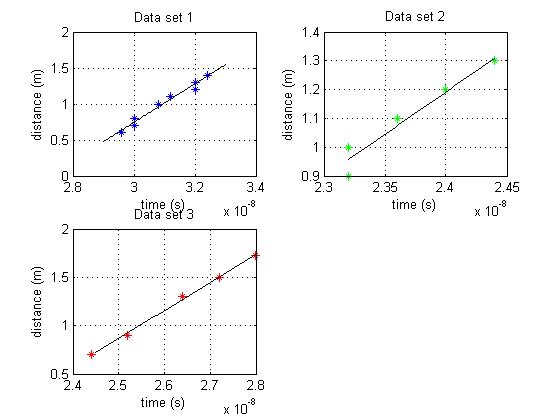
Table 1 to the right shows the results of data set 1, in which the PMT was kept at a voltage of ~600 volts and for changes in distance between PMT and LED of between 60 and 140 cm. The linear fit to this data (as explained in methods) is shown in Figure 2, plot 1. By applying the analysis techniques as described in Methods, we found by taking the slope of the linear least-squares fit that this data set provides a value of c to be [math]\displaystyle{ c=\left(2.68 \pm 0.18\right)\times10^{8} m/s }[/math], which provides an approximation to the accepted value for the speed of light, but not a nearly a good approximation. This set represented our first attempt at data collection on the equipment. Here we attempted to make the changes in distance between the PMT and LED be fairly constant, as can be seen in the first 5 measurements. However the maximum distance we could extend the LED was to 140 cm so once at that point we picked several random points from which to finish the data set. We contribute much of the error in this measurement and likewise this data set to unfamiliarity with the equipment and care taken while making the measurements.
- Table 2:Each row represents a seperate measurement that was made. Column 2 is the PMT voltage chosen to be constant throughout the data set. Column 3 represents the Voltage measured on the Oscilloscope being recieved from the TAC. Column 4 is the recorded change in distance between PMT and LED. Column 5 is the associated time with the voltage output of the TAC.
| Data Set 2 Measurments | PMT Ch1 Voltage | TAC Time delay voltage | Distance (cm) | Time (ns) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.44\pm.04 }[/math] | 70 | 24.4 |
| 2 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.4 \pm.04 }[/math] | 80 | 24 |
| 3 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.36 \pm.04 }[/math] | 90 | 23.6 |
| 4 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.32 \pm.04 }[/math] | 100 | 23.2 |
| 5 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.32\pm.04 }[/math] | 110 | 23.2 |
Table 2 to the right shows the results of data set 2, in which the PMT was kept at a voltage of ~800 volts and for changes in distance between PMT and LED of between 70 and 110 cm. We chose to take several less data points due to the linearity we saw in the collected data. The linear fit to this data (as explained in methods) is shown in Figure 2, plot 2. By applying the analyis techniques as described in Methods, we found by taking the slope of the linear least-squares fit that this data set provides a value of c to be [math]\displaystyle{ c=\left(2.94 \pm 0.42\right)\times10^{8} m/s }[/math], which provides a decent approximation to the accepted value for the speed of light. This set represented our second attempt at data collection on the equipment Here we attempted to make the changes in distance between the PMT and LED be fairly constant, as can be seen in the 5 measurements. We attempted to have a much more linear change in the distances, trying to increment the change in 10 cm intervals. We believe that being more familar with the equipment and using a more constant incrementation of the changes in distance between the PMT and LED led to a much more accurate value of c.
- Table 3:Each row represents a seperate measurement that was made. Column 2 is the PMT voltage chosen to be constant throughout the data set. Column 3 represents the Voltage measured on the Oscilloscope being recieved from the TAC. Column 4 is the recorded change in distance between PMT and LED. Column 5 is the associated time with the voltage output of the TAC.
| Data Set 3 Measurments | PMT Ch1 Voltage | TAC Time delay voltage | Distance (cm) | Time (ns) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.8\pm.04 }[/math] | 27.5 | 28 |
| 2 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.64 \pm.04 }[/math] | 70 | 26.4 |
| 3 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.52 \pm.04 }[/math] | 110 | 25.2 |
| 4 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.44 \pm.04 }[/math] | 130 | 24.4 |
| 5 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.72\pm.04 }[/math] | 50 | 27.2 |
Table 3 to the right shows the results of data set 3, in which the PMT was kept at a voltage of ~720 volts and for changes in distance between PMT and LED of between 27 and 130 cm. This data set was much more chaotic in the changes in distance chosen. The linear fit to this data (as explained in methods) is shown in Figure 2, plot 3. By applying the analyis techniques as described in Methods, we found by taking the slope of the linear least-squares fit that this data set provides a value of c to be[math]\displaystyle{ c=\left(2.89 \pm 0.08\right)\times10^{8} m/s }[/math], which provides a decent approximation to the accepted value for the speed of light. This set represented our third attempt at data collection on the equipment Here we attempted to make the changes in distance between the PMT and LED be more sporatic, as can be seen in the 5 measurements. However in comparison to data set 2, this could show that the steadiness of the incrementation might have a small effect on the accuracy, since we were not a accurate with this data set as compared to data set 2. We still contribute the accuracy we achieved to still more familiarity with the equipment, which gave us a wonderful improvement over data set 1.
- Table 4:Each row represents a seperate measurement that was made. Column 2 is the PMT voltage chosen to be constant throughout the data set. Column 3 represents the Voltage measured on the Oscilloscope being recieved from the TAC. Column 4 is the recorded change in distance between PMT and LED. Column 5 is the associated time with the voltage output of the TAC.
| Data Set 2 Measurments | PMT Ch1 Voltage | TAC Time delay voltage | Distance (cm) | Time (ns) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.16\pm.02 }[/math] | 15 | 31.6 |
| 2 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.26 \pm.02 }[/math] | 30 | 32.6 |
| 3 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.26 \pm.02 }[/math] | 45 | 32.6 |
| 4 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.32 \pm.02 }[/math] | 60 | 33.2 |
| 5 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.36\pm.02 }[/math] | 75 | 33.6 |
| 6 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.44\pm.02 }[/math] | 90 | 34.4 |
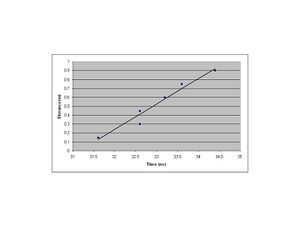
Table 4 to the right shows the results of data set 4, in which the PMT was kept at a voltage of ~640 volts and for changes in distance between PMT and LED of between 15 and 110 cm. For this data set I chose to take 5 measurements. The linear fit to this data (as explained in methods) is shown in Figure 2, plot 2. By applying the analyis techniques as described in Methods, we found by taking the slope of the linear least-squares fit that this data set provides a value of c to be [math]\displaystyle{ c=\left(2.85 \pm 0.03\right)\times10^{8} m/s }[/math], which provides a decent approximation to the accepted value for the speed of light. This set represented our fourth attempt at data collection on the equipment. Here I attempted to make the changes to the experiment as a whole. I moved the entire experimental set up to another position that was more stable, and as discussed above for table 2, made the changes in distance between the PMT and LED be fairly constant, as can be seen in the 6 measurements. I attempted to have a much more linear change in the distances, trying to increment the change in 15cm intervals.I believed that moving the setup to a more stable position that is also more easily accessible and being more consistent in the incrementation of the distances would make this set much more accurate. However, by seeing the value obtained from this set, it is obviously not more accurate. There is some type of systematic error in the experiment that I am unable to account for or detect. As discussed above, I had several ideas of error, and in this set tried to reduce or eliminate them, but our error is even larger in this set than sets 2 and 3. We tried several times at gaining more accurate data for this set but the data only became more and more inaccurate, giving us values of c that were very far off. The data from this set can be seen in figure 3 below.
Results:
I chose to discard data set 1 in favor of sets 2 and 3 due to the error in data set 1. With the much more accurate predictions for the speed of light from data sets 2 and 3 given above, we then proceeded to perform a weighted average of the two values for c (described in Methods) to obtain [math]\displaystyle{ c=\left(2.892 \pm .077\right)\times10^8 m/s }[/math] as my reported value of c and a value of[math]\displaystyle{ c=\left(2.85 \pm .03\right)\times10^8 m/s }[/math] coming from the fourth data set representing a change in the experiment in hope of reducing error, which as can be seen was not accomplished. The first value is a reasonable approximation to the speed of light although still not as near as I would have liked.
5. Conclusions
The reported value of [math]\displaystyle{ c=\left(2.892 \pm .077\right)\times10^8 m/s }[/math] given above is in fair aggreement with the presently accepted value mentioned in the abstract. From our reported value we find that there is a relative error given by [math]\displaystyle{ RE=\frac{\left|2.99\times10^{8}-c\right|}{\left|2.99\times10^{8}\right|}=0.0328=3.3% }[/math] which is a value we would like to see be reduced and obtain a more accurate measurement for the speed of light. Due to time constraints on this experiment we were unable to perform more data collection. I considered the placement of the equipment and possibly unfamiliarity with the equipment as sources of error and for data set 4, I attempted to correct for those and any other possible sources of error such as very inconsistent changes in distance betweent the PMT and LED. However as can be seen from the data set none of these things were able to improve the results, and actually left us with a value of c that is farther off than either of data sets 2 or 3. I took data set 4 several times in hope of obtaining more accurate values, but was not able to do so. The data given above for set 4 is the first and more accurate attempt made for that set. It must be concluded that there is some form of systematic error in the experiment that is not being accounted for. It could be something in the equipment, the set up, how we are taking the data. The error could possibly even be experimenter fatigue. In any case the report value above of [math]\displaystyle{ c=\left(2.892 \pm .077\right)\times10^8 m/s }[/math] is our most accurate value. Due to time constraints and little knowledge of electronics I am unable to determine a way in which the error in the experiment can be reduced or removed(i.e reduced to an ignorable amount).
References/Acknowledgments
1. On Physical Lines of Force - 1861 Maxwell's 1861 paper describing magnetic lines of Force - Predecessor to 1873 Treatise
2. Einstein, Albert,Zur Elektrodynamik bewegter Körper, Annalen der Physik, Berne 1905
3. Louis Essen, Wikipedia Article
4. Essen, L., and Perry, J. V. (1955), "An atomic standard of frequency and time keeping", Nature 176, p. 280.
5. Weighted Averages, Wikipedia Article
6. Dr. Golds Physics 307L lab manual, which can be found here: Previous Course lab manual.
7. EG&G Ortec TAC Operator Manual, which can be found in the Senior Lab
8. Antonio Rivera's Lab Notebook:
lab Notebook.
9. I would like to thank Dr. Koch for his help with the instrumentation and data anslysis.