Physics307L:People/sosa/formallabreport
SJK 14:25, 17 December 2008 (EST)

This is a very good report--if we had gone through the rough draft process, I am sure you would have produced a really excellent final draft. It looks like you did an excellent job on the data acquisition and analysis and also on your background reading and citing of original research papers.
Determining the Elementary Charge Via Millikan's Oil Drop Experiment
Experimentalists: Manuel Franco Jr. and David Sosa
Location: Junior Lab, Department of Physics & Astronomy, University of New Mexico
Albuquerque, NM 87131
dsosa55@unm.eduAbstract
SJK 03:20, 17 December 2008 (EST)

excellent abstract.
The measurement of the fundamental electric charge is of extreme importance for physics because electrons and its characteristics play an essential role in many physical phenomena such as electricity, magnetism, quantum mechanics, thermal conductivity, etc [1].In this experiment we tried to demonstrate the existence of an elementary charge and at the same time attempted to measure its magnitude. In order to achieve these two objectives, we replicated Robert Millikan's oil drop experiment [5]. In this experiment we measure the force on tiny oil droplets suspended against gravity between two metal electrodes. Knowing the electric field, the charge on the droplet could be determined. Although it was well known that electric charge was quantized before Millikan's experiment in 1913 [8], the Millikan experiment provided the most accurate measurement of the electron charge to that day. In the replication of the experiment we used the least squares method to obtain the value [math]\displaystyle{ (1.63\pm 0.02)\times 10^{-19}\;C }[/math] with a difference of [math]\displaystyle{ 2.14%\; }[/math] with the accepted value of [math]\displaystyle{ 1.602\times 10^{-19}\;C }[/math] [7] This result suggests that we were able to replicate Millikan's Experiment.
Introduction
SJK 04:00, 17 December 2008 (EST)

This is a terrific introduction. It probably could be organized better...but it's all so fascinating that I don't think that matters much. Excellent references.
It is difficult to say when the idea of an elementary charge exactly came to be, but Robert Millikan himself gives the credit to Benjamin Franklin for writing about it around 1750 [2]. It was also theorized several times during the 19th century, by a number of physicists including the Irish physicist George Johnstone Stoney, who would name this elementary charge, electron [9]. But it was not until 1887 that Sir Joseph John Thomson obtained the definite experimental proof of the existence of an elementary subatomic particle with negative charge, he would call corpuscle [8]. This experiment would eventually award him with the Nobel Prize in 1906 [10]. After this discovery, Thomson along one of his co-workers J.S.E. Townsend proceeded to measure the charge of the "corpuscles". The result they obtained was [math]\displaystyle{ 1.000\times 10^{-19}\;C }[/math] [3]. Millikan began to work in his oil drop in 1906 and continued for 7 years until he published his final paper in 1913.[3] The oil drop method was superior to the method devised by Thomson and Townsend mainly for 3 reasons:
- Oil evaporates much slower than water, allowing a more consistent measurements.[3]
- Drops can be studied one at the time unlike the water cloud.
- In following the oil drop over many ascents and descents, he could measure the drop as it lost or gained electrons.
With the Oil Drop experiment, Millikan obtained a value of [math]\displaystyle{ 1.592(17)\times 10^{-19}\;C }[/math] for the charge of the electron, which is less than one percent from the actual accepted value of [math]\displaystyle{ 1.602(49)\times 10^{-19}\;C }[/math] [7]. For this report we attempted to recreate Millikan's experiment.
Other Methods to Measure the Elementary Charge
From the Josephson and von Klitzing constants
This method is the most accurate method to measure the elementary charge. This method consists in two effects in quantum mechanics: The Josephson effect, voltage oscillations that arise in certain superconducting structures; and the quantum Hall effect, a quantum effect of electrons at low temperatures, strong magnetic fields, and confinement into two dimensions.[11] [12]
The Josephson constant is:
[math]\displaystyle{ K_J = \frac{2e}{h} }[/math] (where h is Planck's constant).
The von Klitzing constant is
[math]\displaystyle{ R_K = \frac{h}{e^2} }[/math] It can be measured directly using the quantum Hall effect.
From these two constants, the elementary charge can be deduced:
[math]\displaystyle{ e = \frac{2}{R_K K_J} }[/math]
In terms of the Avogadro constant and Faraday constant
The elementary charge can also be determined using the following formula:
[math]\displaystyle{ e=\frac{F}{N_A}\; }[/math]
where
[math]\displaystyle{ F\; }[/math] is Faraday's Constant and it is defined as the amount of charge that must pass through a solution to electrolytically deposit a mole of a singly charged, or monovalent element contained in the solution.
[math]\displaystyle{ N_A\; }[/math] is Avogadro's Constant and it is defined as the number of atoms or molecules contained in a mole, which is defined as a mass in grams equal to the atomic or molecular weight of a substance.
Faraday's constant can be determined using Faraday's 1st law of electrolysis and Avogadro's constant is the number of atoms or molecules needed to make up a mass equal to the substance's atomic or molecular mass, in grams.
Shot noise
Shot noise is when the passing of electron is not a continual random flow, but rather a discrete flow in which electrons pass just one at the time. By carefully measuring the noise of the current, the elementary charge can be measured. [12]
Automated Millikan Oil Drop
This is a modern version of Millikan's Oil Drop experiment. This automated device was used in this paper to search for the fractional charge particles required for unification in all the superstring models. There are clear differences in this new setup and the old one The apparatus uses a digital charged coupled device (CCD) camera interfaced to a computer. It also uses silicone instead of oil, because silicone has a low vapor pressure and the right viscosity to generate stable drops. Also the falling of the drops is controlled by an electric pulse that regulates the falling rate. It is valuable to see how Millikan experiment for determining the charge of the electron is being used to explore the current forefront of physics. [4] [5]
Materials and Methods
SJK 14:12, 17 December 2008 (EST)

these are good methods for an informal report...in your rough draft I would have pointed out changes necessary to make it more appropriate for a formal publication.


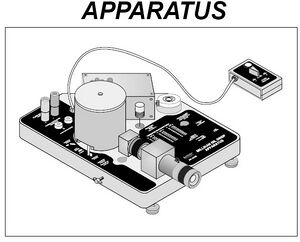
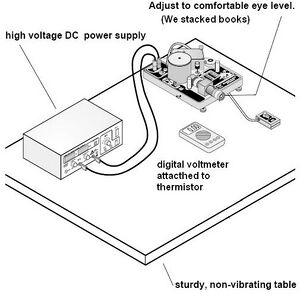
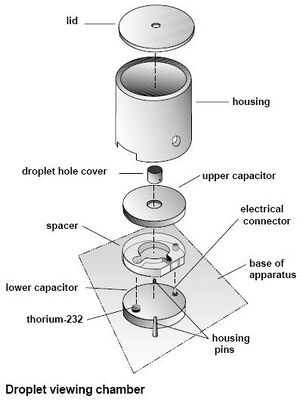
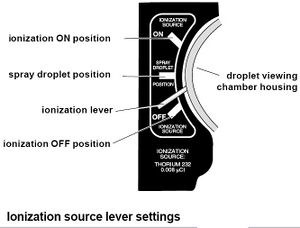
- Millikan oil drop apparatus(PASCO scientific Model AP-8210).
- Tel-Atomic 50V & 500V supply.
- Fluke 111 True RMS Multimeter
- Mineral oil(Squib #5597)
- Atomizer(Included with the apparatus)
- Smiec 0-25mm 0.01mm Micrometer
- Stopwatch
Set Up
First we looked for a comfortable position to set the apparatus, so we could take measurements during 3 straight hours. We used some books to achieve the best position.Although the final position of the apparatus was not entirely comfortable, it did not stop us from continuing. Then, as the manual indicated, we made sure the Millikan apparatus was correctly leveled, by using the leveling gauge and the adjusting feet. Then we used the micrometer to measure the spacer, which is equal to the plate separation.We did not get a good result the first time, as our analysis seemed to indicate, so we went a second time to measure it and with the help of Dr. Koch we obtained the correct measurement. We then opened the Droplet viewing chamber to clean it from left oil from previous experiments.This is important because as Dr. Koch and I would find out, if the chamber is full of oil, the droplets won't be seen. We then reassembled the Droplet viewing chamber according to figure 5
With the lights off we proceeded to calibrate the microscope. First we adjusted the viewing scope and the the vertical filament adjustment knob by unscrewing the focusing wire from its storage place on the platform and inserting it into the hole in the center of the top capacitor plate. According to the manual, the best view is achieved we the light is brightest on the wire in the area of the reticle and when the wire is focused. Manuel and I then connected the power supply on the [math]\displaystyle{ 500 V\; }[/math] side to the plate voltage connectors. We measure to voltage to get exactly [math]\displaystyle{ 500 V\; }[/math]. Then we measured the resistance by connecting the multimeter to the thermistor connectors. We obtained a value of [math]\displaystyle{ 2.09M\Omega\; }[/math]. We would used this value later to obtained the temperature of the room. With these preparations and measurements of constants done, we proceeded to observe the droplets.
Experiment
We prepared the atomizer by spraying oil into a tissue. As Aram instructed us, it is possible to hear when the atomizer is spraying oil or not. One has to pay close attention.We moved the ionization source lever to the Spray Droplet Position to allow air to escape from the chamber. We pointed the atomizer 90° into the chamber, sprayed and slowly released. We should have selected our drops based on the approximate criteria given by the manual;
| Excess Electrons | Fall time (s) | Rise time (s) |
|---|---|---|
| 1 | 15 | 15 |
| 2 | 15 | 7 |
| 3 | 15 | 2 |
but unfortunately we didn't proceed that way. Instead we selected a droplet without any regard for its excess electrons and started taking several measurements of it fall and rise times.
Data and Analysis
SJK 14:21, 17 December 2008 (EST)

I looked at your Excel sheet and it looks like you did a very careful and good analysis. The grouping assignment is a key to the experiment and definitely more discussion of that would be warranted in this report.
The complete data taken during this experiment and also the analysis can be seen in this Excel Spreadsheet
We analyzed out data first by obtaining the fall and rise time for all the measurements we made. We used the straightforward formula [math]\displaystyle{ V=\frac{d}{t} }[/math]. We were able to use this formula because the droplets reach terminal velocity quickly and therefore travel at a constant rate after that.
To find the elementary charge we first found the radius of the droplet by using the formula:
[math]\displaystyle{ a=\sqrt{\left(\frac{b}{2 p}\right)^2+\left(\frac{9\eta v_f}{2g\rho}\right)}-\frac{b}{2p} }[/math]
Knowing the radius and with the density of oil given, it was straightforward to get the mass of each drop:
[math]\displaystyle{ m=\frac{4}{3}\pi a^3 \rho }[/math]
With the mass of the droplet, we calculated the charge carried by each droplet with:
[math]\displaystyle{ q=\frac{mg(v_f+v_r)}{Ev_f} }[/math]
Plugging everything we obtain:
[math]\displaystyle{ q = {\frac{4}{3}}\pi \rho g[\sqrt{(\frac{b}{2p})^2 +\frac{9 \eta v_f}{2g\rho}}-\frac{b}{2p}]^3\frac{v_f + v_r}{Ev_f} }[/math]
The symbols presented in the previous equations are:
[math]\displaystyle{ q\; }[/math] The charge of the electron
[math]\displaystyle{ p\; }[/math] Barometric pressure = [math]\displaystyle{ 8.33\times 10^{4}Pa\; }[/math]
[math]\displaystyle{ d\; }[/math] Distance between capacitor plates [math]\displaystyle{ 7.59mm\; }[/math]
[math]\displaystyle{ g\; }[/math] Acceleration due to gravity- [math]\displaystyle{ 9.8 \frac{m}{s^2} }[/math]
[math]\displaystyle{ b\; }[/math] Constant [math]\displaystyle{ 8.44\times 10^{-3} Pa\; }[/math]
[math]\displaystyle{ a\; }[/math] Radius in drop measured in meters
[math]\displaystyle{ \rho = 886 \;\frac{kg}{m^3} }[/math] Mineral Oil density
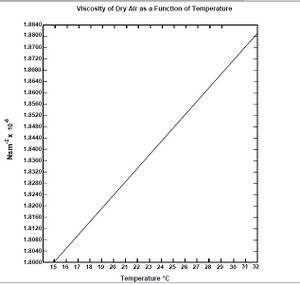
[math]\displaystyle{ \eta\; }[/math] Viscosity of air
[math]\displaystyle{ V\; }[/math] Potential difference across the plates in Volts
[math]\displaystyle{ v_r\; }[/math] Rise velocity
[math]\displaystyle{ v_f\; }[/math] Falling velocity
[math]\displaystyle{ E\; }[/math] Electric field (found with [math]\displaystyle{ \frac{V}{d}) }[/math]
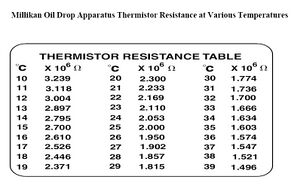
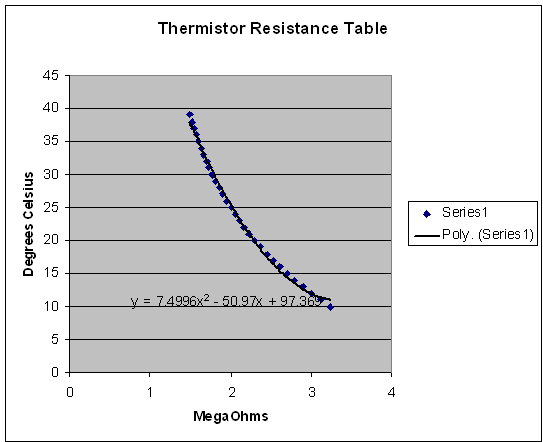
When we finally obtain a charge for the for each drop by relating all the constants and previously obtained values, we can get an average charge for each electron. Looking at this charge, we can assign a multiple of [math]\displaystyle{ -e\; }[/math] to each one. I assigned a multiple of to each of these measured charges. I also obtained an average when several measurements were made for the same drop. I also had to change the calculations in order to account for the change in temperature that we measure two different days. Because we made measurements two different days, we have to different temperatures for each day. Since the temperature was not exactly as given in the Thermistor Resistance Table it was necessary to plot that data and the insert our values for the resistance to get the temperature for the two day. Once I had the temperature, I used this online Gas Viscosity Calculator to get the viscosity for each day. It was not necessary to use Figure 8. Also the barometric pressure for each day is going to be different. I looked for the different barometric pressures for each day in Albuquerque here. I used Excel to organaize and process all the data taken. I used the Excel command Linest to obtain the value of the elementary charge. I also used the Polyfit command to obtain the values of the temperature according to the resistance each day Figure 9 .
Results and Discussion
SJK 14:23, 17 December 2008 (EST)

Of course in a formal publication there would be much more text in this section...if this were your rough draft, I'd give some ideas for you here.
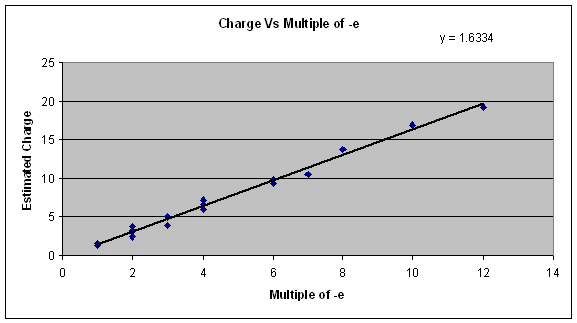
The result obtained using Linear Regression was [math]\displaystyle{ (1.63\pm 0.02)\times 10^{-19}\;C }[/math] with a difference of [math]\displaystyle{ 2.14%\; }[/math] with the accepted value of [math]\displaystyle{ 1.602\times 10^{-19}\;C }[/math]. This result suggests that we were able to replicate Millikan's experiment succesfully.
Acknowledgments
First and foremost I would like to thank Dr. Koch for teaching this course and helping us learn more about experimental physics. I also would like to thank Lab Assistant Aram Gragossian for his helpful inputs in the experiments. I also thank my lab parter Manuel Franco JR who was crucial in the achievement of a good result for this experiments. In addition, I thank Linh Le from last year for his contribution in this experiment. I would also like to thank all my partners from this year, because I used many of their ideas and feedback to complete my formal report.
References
SJK 14:24, 17 December 2008 (EST)

There are a bunch of really good references here! I hope you had fun looking them over, and I wish I had more time to read all of them.
[1] How atoms work http://science.howstuffworks.com/atom.htm
[2] The electron and the light-quant from the experimental point of view ,Nobel Lecture, May 23, 1924 http://nobelprize.org/nobel_prizes/physics/laureates/1923/millikan-lecture.pdf
[3] Determination of the Charge on an Electron http://dbhs.wvusd.k12.ca.us/webdocs/AtomicStructure/Determine-electron-charge.html
[4] D. Loomba et. al, Search for Free Fractional Electric Charge Elementary Particles Using an Automated Millikan Oil Drop Technique, 1999. http://prola.aps.org/pdf/PRL/v84/i12/p2576_1
[5] Millikan R.A, On the elementary electrical charge and the Avogadro constant, 1913 http://authors.library.caltech.edu/6438/1/MILpr13b.pdf
[6] Quarter Electrons May Enable Exotic Quantum Computer, Scientific American,2008 http://www.sciam.com/article.cfm?id=quarter-electrons-may-enable-quantum-computer
[7] Official value of the elementary charge. http://physics.nist.gov/cgi-bin/cuu/Value?e
[8] Thomson J.J ,Cathode Rays, Philosophical Magazine, 44, 293, 1897. http://web.lemoyne.edu/~GIUNTA/thomson1897.html
[9] Of the "Electron" or Atom of Electricity, G. Johnstone Stoney, 1894. http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Stoney-1894.html
[10] J.J. Thomson ,The Nobel Prize in Physics 1906, Nobel Lecture http://nobelprize.org/nobel_prizes/physics/laureates/1906/thomson-lecture.html
[11] B. D. Josephson. The discovery of tunnelling supercurrents. Rev. Mod. Phys. 1974; 46(2): 251-254. http://prola.aps.org/abstract/RMP/v46/i2/p251_1
[12] Ando, Tsuneya; Matsumoto, Yukio; Uemura, Yasutada (1975). "Theory of Hall Effect in a Two-Dimensional Electron System". J. Phys. Soc. Jpn. 39: 279–288. doi:10.1143/JPSJ.39.279.
[13] Horowitz, Paul and Winfield Hill, The Art of Electronics, 2nd edition. Cambridge (UK): Cambridge University Press, 1989, pp. 431-2.