Physics307L:People/Mondragon/Notebook/071017
data for planck's constant
SETTLE VOLTAGE FOR YELLOW ORANGE:=652mV
stop=612mv
1.28s @100%
1.20s @80%
1.72s @60%
2.04s @40%
4.92s @ 20%
SETTLE VOLTAGE FOR GREEN:=800mV
STOP=712mV
1.40s @100%
2.10s @80%
2.50s @ 60%
4.90s @40%
12.0s @20%
SETTLE VOLTAGE FOR BLUE;=1.37V
STOP=1.23V
1.20s @ 100%
2.00s @ 80%
2.00s @60%
2.80s @ 40%
7.40s @ 20%
Settle voltage for purple=1.50V
stop=1.34V
1.28s @100%
1.40s @80%
1.56s @60%
1.92s @40%
5.76s @20%
settle for UV=1.80V
stop=1.62V
6.2s @100%
6.4s @80%
9.7+/-2.0s @60%
17.4s @40%
81s @20%
Methodology
Following instructions in Dr. Gold's lab manual, I made sure the equipment was set up correctly to perform the experiment. First, one should get the light from the lamp as focused as possible by adjusting the diffraction grating/lens. Next, one should make sure light from the lamp reaches the photocathode of the [math]\displaystyle{ \tfrac{h}{e} }[/math] apparatus. How to do this is described in the manual. (perhaps I should upload the manual in case www-hep.unm.edu goes down again) following that, one should test the batteries of the [math]\displaystyle{ \tfrac{h}{e} }[/math] apparatus. I suppose the minimum ratings for the batteries are listed were the apparatus's test points are, so they are +6V and -6V. Measure using a multimeter from the apparatus's ground to each of the battery test points. I measured +8.70V and -8.69V, so the batteries were fine.
All of the outputs of the [math]\displaystyle{ \tfrac{h}{e} }[/math] device are made for banana clips. The lab manual suggests using a stopwatch and a multimeter to measure the rise time. But, since we wanted to use an oscilloscope to measure rise time more accurately, we has to use a banana to BNC connector. It seems like the connector, and maybe the BNC cable and the BNC input of the oscilloscope, caused some weirdness in the voltage output.
If the quantum description of light was correct, then for a certain light frequency [math]\displaystyle{ f }[/math] the voltage output from the apparatus would rise exponentially and settle to a stopping voltage [math]\displaystyle{ V_o(f) }[/math] like the voltage across a capacitor would rise as the capacitor was charging. When we where using just the multimeter this definitely seemed like the case. But, when we had the voltage output going to the oscilloscope, the voltage often exhibited a very sharp rise followed by either an exponential decay to some voltage [math]\displaystyle{ V \gt V_o(f) }[/math] or a sharp drop followed by an exponential rise and settle to [math]\displaystyle{ V_o(f) }[/math].
Theory
The [math]\displaystyle{ \tfrac{h}{e} }[/math] apparatus is basically a capacitor. One plate is a photocathode. Light shining on the photocathode gives electrons the energy necessary to escape the surface of the cathode and to possibly cross the gap to the anode. As charge builds up on the anode, the voltage across the capacitor will increase, as will the energy necessary for electrons to cross the gap.
Just for future reference, I doubt I'll be using it though [math]\displaystyle{ q=C*V }[/math], where [math]\displaystyle{ q }[/math] is the absolute value of charge on one plate of the capacitor, [math]\displaystyle{ V }[/math] is the absolute value of the voltage across the capacitor, and [math]\displaystyle{ C }[/math] is the capacitance of the capacitor.
The energy needed by an electron to escape the photocathode's surface is [math]\displaystyle{ W_0 }[/math]. [math]\displaystyle{ W_0 }[/math] is a property of the photocathode. After light imparts its energy onto en electron, part of the energy will be used to escape the photocathode (if [math]\displaystyle{ E_{light} \ge W_0 }[/math]), and the rest manifests itself as the kinetic energy of the now free electron, [math]\displaystyle{ KE_{max} }[/math]. [math]\displaystyle{ E_{light} = W_0 + KE_{max} }[/math]
Because of the voltage across the capacitor, [math]\displaystyle{ KE_{max} }[/math] must be more than a certain potential energy [math]\displaystyle{ PE_{gap} }[/math] created by the voltage difference. The potential energy that needs to be overcome is proportional to the voltage difference. When [math]\displaystyle{ PE_{gap} \ge KE_{max} }[/math], electrons can no longer reach the anode so the voltage no longer rises. This final voltage is called [math]\displaystyle{ V_{stop} }[/math]. Because of the way capacitors charge, [math]\displaystyle{ V_{stop} }[/math] is never actually reached in a finite amount of time. [math]\displaystyle{ V_{stop} }[/math] is proportional to [math]\displaystyle{ KE_{max} }[/math].
Electrons can only make it to the anode if [math]\displaystyle{ KE_{max} \lt PE_{gap}= e\,V }[/math]. [math]\displaystyle{ KE_{max} }[/math] should, in this experiment, stay the same thoughout a test, but [math]\displaystyle{ PE_{gap} }[/math] changes as [math]\displaystyle{ V }[/math] changes. When [math]\displaystyle{ V_{stop} }[/math] is reached, it is because [math]\displaystyle{ KE_{max} = PE_{gap}= e\,V_{stop} }[/math]
[math]\displaystyle{ \begin{align} E_{light} &= W_0 + KE_{max}\\ E_{light} &= W_0 + e\,V_{stop}\\ \frac{E_{light}}{e} &= \frac{W_0}{e} + V_{stop}\\ \end{align} }[/math]
According to the particle theory of light, the energy imparted by light is proportional to the frequency of the light, the constant of proportionality being Plank's constant. According to the wave theory of light, the energy imparted by light is proportional to the square root of the intensity of the light. The data shows that the stopping voltage doesn't change when the light intensity changes, but it does when the light frequency changes. So
[math]\displaystyle{ \begin{align} E_{light} &= W_0 + KE_{max}\\ E_{light} &= W_0 + e\,V_{stop}\\ \frac{E_{light}}{e} &= \frac{W_0}{e} + V_{stop} &= \frac{h\nu}{e}\\ V_{stop} &= \frac{h\nu}{e} - \frac{W_0}{e}\\ \end{align} }[/math]
ν is the frequency of the light falling on the photocathode and [math]\displaystyle{ h }[/math] is Plank's constant.
table!!
| color | frequency | settle voltage |
|---|---|---|
| Yellow | [math]\displaystyle{ 5.18672*10^{-14} }[/math] Hz | 652 mV |
| Green | [math]\displaystyle{ 5.48996*10^{-14} }[/math] Hz | 800 mV |
| Blue | [math]\displaystyle{ 6.87858*10^{-14} }[/math] Hz | 1.37 V |
| Violet | [math]\displaystyle{ 7.40858*10^{-14} }[/math] Hz | 1.50 V |
| Ultraviolet | [math]\displaystyle{ 8.20264*10^{-14} }[/math] Hz | 1.80 V |
fit is [math]\displaystyle{ V_{stop}=\tfrac{h}{e}*\nu+\tfrac{W_0}{e} \, \, , \,\tfrac{h}{e}=0.377989*10^{-14}\pm 0.014521*10^{-14} \,V*s \,\tfrac{W_0}{e}=-1.282910 \pm 0.097743\,V }[/math]
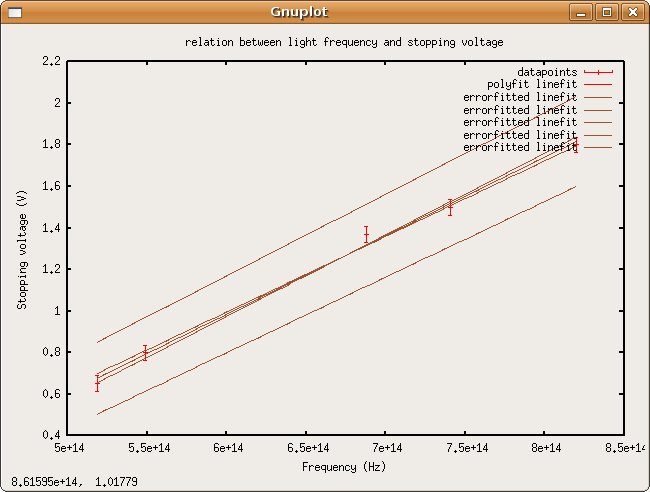
so, [math]\displaystyle{ h=3.77989*10^{-15}\pm 0.14521*10^{-15} \,eV*s }[/math] and [math]\displaystyle{ W_0=1.282910 \pm 0.097743\,eV }[/math]. The accepted value of [math]\displaystyle{ h }[/math], [math]\displaystyle{ h =\,\,\, 6.626\ 068\ 96(33) \times 10^{-34}\ \mbox{J}\cdot\mbox{s} \,\,\, = \,\,\, 4.135\ 667\ 33(10) \times10^{-15}\ \mbox{eV}\cdot\mbox{s} }[/math] is within three standard deviations of my calculated value. Looks like a systematic error.