Physics307L:People/McCoy/Speed of Light/Word
<head> <meta http-equiv=Content-Type content="text/html; charset=windows-1252"> <meta name=Generator content="Microsoft Word 12 (filtered)"> <style> </style>
</head>
<body lang=EN-US>
Raw Data and calculations of mean and standard deviation......................................................... 1
Determination of Voltage difference for known Time delay........................................................ 3
Calculation of Voltage difference for set length difference.......................................................... 4
Calculation of Speed of Light from voltage/time relationship and................................................ 5
Calculation of minimum and maximum values using error in oscilloscope.................................. 6
Calculation of minimum and maximum values within 1 standard deviation of mean................... 7
<a name="_Toc210396835">Raw Data and calculations of mean and standard deviation</a>
calibration_voltage=[1.84 2.24 2.36 2.20
.960 1.44 1.84 2.24
2.08 1.52 1.88 1.48
1.28 1.36 1.68 2.04
1.72 1.92 1.94 1.76
1.60 2.08 1.64 2.04
1.36 1.76 1.32 1.76
1.12 1.56 1.92 1.88
1.64 2.00 1.44 1.52
1.16 1.72 1.84 1.80
1.12 1.56 2.20 2.00
1.48 1.72 1.56 1.92
1.64 1.60 1.88 1.64
1.28 1.44 1.52 1.76
1.48 1.36 2.08 1.96
.960 1.72 2.16 1.88
.800 1.96 1.64 1.84
1.24 1.48 1.92 1.72
1.40 1.76 1.76 2.08
1.42 1.44 1.60 2.16];
calibration_average=mean(calibration_voltage)
calibration_deviation=std(calibration_voltage)
test_voltage=[.860 1.06 1.32 1.60 1.48
1.18 1.02 1.30 1.32 1.60
.940 1.12 1.00 1.02 1.60
1.08 1.60 1.68 1.52 1.28
.940 .780 1.32 1.12 1.52
1.04 1.34 1.22 1.30 1.92
.840 1.28 1.40 1.60 1.32
.820 1.14 1.56 1.48 1.46
.900 .920 1.44 1.56 1.24
1.10 1.08 1.40 1.30 2.06
1.36 1.42 1.48 1.36 1.28
.880 1.28 1.10 1.48 1.56
1.28 1.06 1.10 1.22 1.74
.920 1.32 1.60 1.50 1.38
.840 1.58 1.34 1.58 1.64
1.36 1.08 1.46 1.56 1.82
.760 .840 1.26 1.38 1.38
1.00 .860 1.40 1.66 1.34
1.22 1.14 1.50 1.62 1.58
1.24 1.34 1.22 .980 1.38];
test_average=mean(test_voltage)
test_deviation=std(test_voltage)
calibration_average =
1.3790 1.6820 1.8090 1.8840
calibration_deviation =
0.3192 0.2521 0.2663 0.2112
test_average =
1.0280 1.1630 1.3550 1.4080 1.5290
test_deviation =
0.1888 0.2301 0.1741 0.2020 0.2237
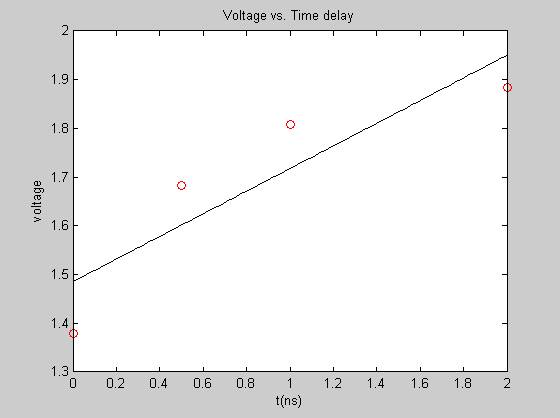
<a name="_Toc210396836">Determination of Voltage difference for known Time delay</a>
t_delay=[0 .5 1 2];
calibration_fit=polyfit(t_delay,calibration_average,1)
t_cal_fit=linspace(0,2,100);
v_cal_fit=polyval(calibration_fit,t_cal_fit);
figure
plot(t_delay,calibration_average,'ro',t_cal_fit,v_cal_fit,'k');
xlabel('t(ns)'),ylabel('voltage'),title('Voltage vs. Time delay');
calibration_fit =
0.2323 1.4852
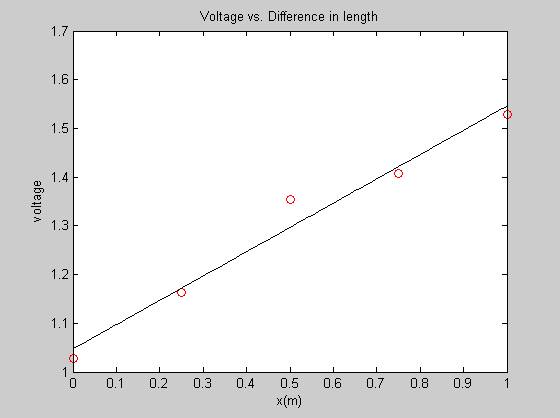
<a name="_Toc210396837">Calculation of Voltage difference for set length difference</a>
x_difference=[0.00,.25,.50,.75,1.00];
length_fit=polyfit(x_difference,test_average,1)
x_fit=linspace(0,1,100);
v_test_fit=polyval(length_fit,x_fit);
figure
plot(x_difference,test_average,'ro',x_fit,v_test_fit,'k');
xlabel('x(m)'),ylabel('voltage'),title('Voltage vs. Difference in length');
length_fit =
0.4988 1.0472
<a name="_Toc210396838">Calculation of Speed of Light from voltage/time relationship and</a>
voltage/length relationship
c_mpns=calibration_fit(1)/length_fit(1) %the units of the calibration
%fit are volts/nanosecond, and those of the length fit are volts/meter
c=c_mpns*1e9
c_mpns =
0.4658
c =
4.6580e+008
<a name="_Toc210396839">Calculation of minimum and maximum values using error in oscilloscope</a>
Margin of error in oscilloscope calculations = .02V Minimum slope would be found with maximum value(n+.02) for data less than median and minimum value (n-.02) for data greater than median minimum L/T = minimum -> L=minimum, T=maximum
t_scope_min(1:2)=calibration_average(1:2)+.02;
t_scope_min(3:4)=calibration_average(3:4)-.02;
V_t_min=polyfit(t_delay,t_scope_min,1)
L_scope_max(1:2)=test_average(1:2)-.02;
L_scope_max(3)=test_average(3);
L_scope_max(4:5)=test_average(4:5)+.02;
V_L_max=polyfit(x_difference,L_scope_max,1)
c_scope_min=abs(V_t_min(1)/V_L_max(1)*1e9)
% maximum
% L/T = maximum -> L=maximum, T=minimum
t_scope_max(1:2)=calibration_average(1:2)-.02;
t_scope_max(3:4)=calibration_average(3:4)+.02;
V_t_max=polyfit(t_delay,t_scope_max,1)
L_scope_min(1:2)=test_average(1:2)+.02;
L_scope_min(3)=test_average(3);
L_scope_min(4:5)=test_average(4:5)-.02;
V_L_min=polyfit(x_difference,L_scope_min,1)
c_scope_max=abs(V_t_max(1)/V_L_min(1)*1e9)
V_t_min =
0.2095 1.5052
V_L_max =
0.5468 1.0232
c_scope_min =
3.8311e+008
V_t_max =
0.2552 1.4652
V_L_min =
0.4508 1.0712
c_scope_max =
5.6610e+008
<a name="_Toc210396840">Calculation of minimum and maximum values within 1 standard deviation of mean</a>
Margin of error = 1 standard deviation Minimum slope would be found with maximum value(n+sd) for data less than median and minimum value (n-sd) for data greater than median minimum L/T = minimum -> L=minimum, T=maximum
t_sd_min(1:2)=calibration_average(1:2)+calibration_deviation(1:2);
t_sd_min(3:4)=calibration_average(3:4)-calibration_deviation(3:4);
V_tsd_min=polyfit(t_delay,t_sd_min,1)
L_sd_max(1:2)=test_average(1:2)-test_deviation(1:2);
L_sd_max(3)=test_average(3);
L_sd_max(4:5)=test_average(4:5)+test_deviation(4:5);
V_Lsd_max=polyfit(x_difference,L_sd_max,1)
c_sd_min=abs(V_tsd_min(1)/V_Lsd_max(1)*1e9)
% maximum
% L/T = maximum -> L=maximum, T=minimum
t_sd_max(1:2)=calibration_average(1:2)-calibration_deviation(1:2);
t_sd_max(3:4)=calibration_average(3:4)+calibration_deviation(3:4);
V_tsd_max=polyfit(t_delay,t_sd_max,1)
L_sd_min(1:2)=test_average(1:2)+test_deviation(1:2);
L_sd_min(3)=test_average(3);
L_sd_min(4:5)=test_average(4:5)-test_deviation(4:5);
V_Lsd_min=polyfit(x_difference,L_sd_min,1)
c_sd_max=abs(V_tsd_max(1)/V_Lsd_min(1)*1e9)
V_tsd_min =
-0.0624 1.7665
V_Lsd_max =
1.0016 0.7972
c_sd_min =
6.2296e+007
V_tsd_max =
0.5271 1.2039
V_Lsd_min =
-0.0040 1.2972
c_sd_max =
1.3084e+011
</body>
</html>