Physics307L:People/Josey/Final Draft
Steve Koch 21:29, 14 December 2010 (EST):Overall, excellent report!
Measuring and Predicting Background Radiation Using Poisson Statistics
Experimentalists: Brian P Josey and Kirstin G G Harriger
Junior Lab, Department of Physics & Astronomy, University of New Mexico
Albuquerque, NM 87131
bjosey@unm.eduAbstract
In this paper, the rate of background radiation was measured with differing time intervals over which the measurements took place. The fact that this data followed the Poisson distribution was demonstrated. After establishing the Poisson distribution, the results of the data were then used to predict the average rate of radiation per second. This estimated value was found to be 30 ± 4 radiations per second. A new set of data was generated from a run representing the rate for radiation per second. This data indicated that the average rate in the laboratory to be 30 ± 5 radiations per second, indicating that the technique is useful to model and measure background radiation. This technique was then further applied to measuring the radiation rate of two gamma-ray sources, Co-60 and Cs-137, determining rates of 560 ± 20 and 1400 ± 40 radiations per second, respectively. These samples also followed a Poisson distribution.
Introduction
The Poisson distribution, first described by Siméon Denis Poisson in 1838 1, is used to describe events that occur in discrete numbers at random and independent intervals, but at a definitive average rate. Examples of this are radiation from nuclei over a range of time, number of births in a maternity ward over time2, or movement of microorganisms 3. Mathematically, the Poisson distribution is given as:
[math]\displaystyle{ P_{\mu} (\nu) = e^{-\mu} \frac {\mu ^ {\nu}} {\nu !} }[/math]
where,
- Pμ (ν) - is the probability of ν counts in a definitive interval, and
- μ - is mean number of counts in the time interval,
This distribution has the unique property that the square root of the average is also the standard deviation 2.
Here the Poisson distribution was demonstrated by measuring the background radiation in a standard physics teaching laboratory at 5000 ft elevation. The background radiation being the naturally occurring ambient radiation in the atmosphere. This radiation is the result of several sources, such as cosmic rays, naturally occurring radioactive isotopes, and fallout from nuclear weapons 4. Several sets of data were created by varying the size of the time interval of the radiation, referred to as the "window size." After taking several different sets of data with the window size ranging from 10 ms to 800 ms, the average rate per second was calculated, and then compared to data taken from a set of 1 second time interval measurements.
The radiation rates where then measured for two radioactive sources not commonly found in nature. The first was a sample of cobalt-60, which has a half-life of 5.27 years 5. The second was a sample of cesium-137, which has a half-life of 30.1 years 6. Both of these sources are manufactured radioactive isotopes that do not occur naturally and are gamma-ray emitters.
Methods and Materials


For this experiment, a combined scintillator-photomultiplier tube (Tracor Norther Model TN-1222) referred to in this paper as scintillator-PMT, Figure 1 was used to collect data7. To do this, every time the scintillator detected ions generated by radiation, it would fire a beam of ultraviolet light to the PMT. The PMT would then convert this light signal into a single voltage pulse. This voltage would be carried to an internal MCS card in a computer (J and J Workstation, with Intel Celeron CPUs of 2.26GHz and 2.27GHz, and 1.96 GB of RAM), where it would be analyzed by a UCS 30 software (Spectrum Techniques UCS 30 software). This software would then count each signal voltage it received, and create a set of data containing both the time interval the data was collected, and the number of times it received a signal voltage in a specific time interval. When the UCS 30 software generated a set of data, it would be saved into a data file that could be manipulated and processed using MATLAB v. 2009a. In order for the scintillator to detect the radiation, it needed a potential gradient that would pick up the ions created in the radiation event. This potential was supplied by a Spectech Universal Computer Spectrometer power supply, Figure 2, and set to 1200 V throughout the course of the experiment.SJK 21:12, 14 December 2010 (EST)

Still think you're a little off on the workings of the scintillator-PMT
To demonstrate the Poisson distribution, the scintillator-PMT, power supply, and computer were all turned on. The UCS 30 software was then uploaded, and the dwell time the software would measure the number of radiations was set to various lengths of time. Data was collected over a series of different time intervals that were set at 10, 20, 40, 80, 100, 200, 400 and then 800 ms. Each run contained 2064 windows of the given size. All of these runs had the same settings, 1200 V from the power supply, and using the MCS internal configuration, and varied only in their time interval length. The data was then analyzed, see results and discussion below, to demonstrate that background radiation did follow a Poisson distribution. This data was then used to predict the behavior of a similar set of data that occurred for a 1 second window size. After predicting its behavior, the system was ran again, using a 2064 intervals of 1 second length. This data was then compared to the predicted results form the initial data.
After the background radiation rate was measured, the radiation rates for two gamma-ray emitters, Co-60 and Cs-137, was measured. To do this, the background radiation was again measured in the way described above to account for any changes due to the elapsed time between these two parts of the experiment. However, for this measurement, data was collected for only 10, 20, 100, and 400 ms for the time interval. Then a cobalt-60 gamma-ray source (1.057 uCi, Isotope Products Laboratories, lot # 519-2-2, produced 20 Jan 96) was placed flat at the PMT side of the scintillator-PMT, approximately half an inch away. The radiation rates was then measured using window sizes of 20, 40, 100 and 400 ms. From this, the data was shown to follow a Poisson distribution, and the average radiation rate per second was calculated. This procedure was then repeated for a similar sample of cesium-173 (1.073 uCi, Isotope Products Laboratories, lot # 519-3-1, produced 20 Jan 96), illustrating the Poisson distribution in the process, and determining the average radiation rate per second.
Results
Note: all of the raw data for this report, and some of the MATLAB code, can be accessed here. Warning, the page takes a while to load. SJK 21:14, 14 December 2010 (EST)

Excellent open data! (Matlab code seems to be missing)
From the scintillator-PMT and the UCS 30 software, the data was processed using Google Docs to determine the range of the number of radiation events per window, and the number of windows with the given number of radiation events. A fractional distribution of the data was also determined. This data is summarized in Table 1 below:
- Table 1 This table summarizes the raw data from each of the initial experimental runs. For each window size, the whole range of number of radiation events per window is given in the first column. In the second column, the number of windows that had this given number of radiation events is given. For example, for the 10 ms run, only a single window had four radiation events in it. The third and final column gives the fractional probability, out of 1, of such event happening in the given run.

From this data, a graph was generated to illustrate the characteristics of the data. This graph is given in Figure 3. For the sake of simplicity only four of the nine data runs are graphed, however, even from this small sample of data, the trends across the whole of the sample are still clear. While the exact implications of this data is discussed in the discussion section below, the data makes it clear that as the window sizes increases, the most probable number of radiations per window increases, and the distribution of the probabilities spreads. This spreading in the data is a result of a greater standard error. Together these two trends are qualitative reasons to believe that the data follows a Poisson distribution. This is further discussed bellow in the discussion section2.
A more potent argument for the Poisson distribution is to determine the averages and standard deviations for each set of data. This data is summarized in Table 2 below:
- Table 2 This table summarizes the raw data collected from the runs with varying window sizes, from 10 ms to 800 ms. The first column represents the average radiation event per window as calculated directly from the data. The second and third rows represent the standard deviation of the data as the square root of the average, and as directly calculated from the data. The fourth row represents the percent error of the standard deviation from the data from the square root standard deviation. Because of the very low difference, it is clear that the data follows a Poisson distribution. The last two rows are the average and standard deviation converted from window size to rate per second.
As this table illustrates, the average radiation event per window sizes grows as the window sizes increases, and the standard deviation in proportion to the average also increases. There are two standard deviations in the table. The first is the square root of the average, while the second is directly calculated from the data. The reason for this, discussed in greater detail below, is that the standard deviation of a Poisson distribution is identical to the square root of the average. As the percent error between the two values shows, the data does follow this trend very closely, and the small differences, that never exceed 1.5 %, indicate that this is true.
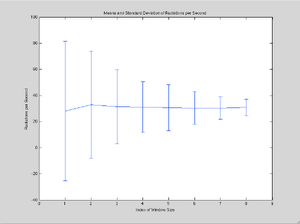
The averages and standard deviations from the data were then divided by the window size to give the rate and error as number of radiations per second. These values are then graphed in Figure 4. Clearly the standard deviation decreases as the window size approaches 1 second, indicating the greater accuracy in the data. From this data, the average rate and standard deviation for a windows size of 1 second was calculated. This value, xwav, was calculated using weighted averages2:
[math]\displaystyle{ x_{wav} = \frac {\sum {w_i x_i}} {\sum {w_i}} }[/math]
where
- xwav - is the best estimate for the average number of radiations per second,
- wi - is the weight of each average, this value is just the inverse of the square of the standard error for a given run,
- xi - is the average value from each run
The standard deviation is then given as:
[math]\displaystyle{ \sigma_{wav} = \frac {1} {\sqrt {\sum {w_i}}} }[/math]
where again, wi is the weight of each average, and σwav is the best estimate for the standard deviation in the final average. These calculations then give a predicted value of 30 ± 4 radiations per second. Another experiment was ran, this time the window size was raised to 1 second. The data from this experiment is summarized in Table 3 below. It is important to note that the predicted value for the average number of radiations per second is only off by the measured value by 0.725 %.
- Table 3 This table summarizes the data taken for a window size of 1 second. On the left is the average predicted by the calculations, its square root, and predicted standard deviation. Below this is the actual average, its square root, standard deviation and the percent difference between the prediction and the measured amount. On the left is the range of radiations per minute, the raw number of windows with a given number and their fractional frequency.
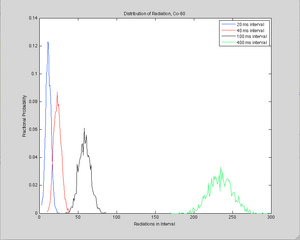

From the second set of measurements, we were able to determine the average rate of radiation per second for the background in the same way as given above, giving a rate of 24 ± 5 radiations per second. While this value is slightly less than the one from the original experiment, possibly from change of conditions over the weeks between the experiments, the nature of this change is outside of this paper, and is only used as a baseline for our cobalt and cesium measurements. As summarized in Table 4 below, both of the gamma-ray sources exhibited a growth in average rate and standard deviation as the measurement dwell time increased. This is illustrated in Figure 5 and Figure 6 for cobalt and cesium respectively. From the data, it was determined that cobalt-60 had an average rate of 560 ± 20 radiation per second, approximately twenty three times greater than the background. Similarly, the cesium-137 sample had an average radiation rate of 1400 ± 40 radiations per second, nearly sixty times greater than the background.
- Table 4 This table summarizes the data from second background measurement and the measurements for both cobalt-60 and cesium-137. For each measurement, the average rate per dwell time is given, as well as the square root standard deviation, and experimental standard deviation, which are used to establish the Poisson distribution, through their percent differences. Also, the average rate per second per trial, and per sample is given. For the cesium and cobalt samples, the background radiation has also been subtracted.
Discussion
Qualitatively, the Poisson distribution has a specific trend in its behavior, namely, as the window size over which the counts were taken increases, the average number of events per window increases, and the distribution spreads out over time8. This results in probability graphs moving to the right and flattening in a standard x-y graph as Figure 3 demonstrates. This behavior in the data indicates that a Poisson distribution could be the mostly likely way to model and represent the data. However, there is a much stronger argument for this conclusion.
The qualitative behavior in the Poisson distribution is actually the result of the change in the standard deviation from the mean2,8. As Table 2 illustrates, the square root of the mean is close enough to the experimental deviation. In fact, using the theory of large numbers, it can be shown that the standard deviation of a Poisson distribution and the square root of the mean are the same2. The data for the first several experimental runs illustrates that the standard deviation and square root of the mean never differ by more than 1.3 %, indicating a very close relationship. This relationship is so close that it is clear that the background radiation in the laboratory can be modeled by a Poisson distribution. Also, this means that as the mean number of radiations per window increases, the standard deviation increases proportional to the square root of the mean, giving the spreading behavior in Figure 3.
Armed with this knowledge of the behavior of the background radiation, the means and standard deviations for the experimental sets between 10 ms and 800 ms were used to determine the average rate of radiation per second. As discussed in the results section, this value was found by using the weighted average method to account for varying degrees of certainty in the measurements. This generated a value of 30 ± 4 radiations per second, and the experimental test for the one second time window gave a final result of 30 ± 6 radiations per minute. As summarized in Table 3 the difference between the two values was only 0.725 %. Because of this close relationship between the two values, it is clear that the method of applying the Poisson distribution to calculate the average radiation rate is successful. This can then be used for any other window size, where determining the final result is only a function of scale.SJK 21:19, 14 December 2010 (EST)

I still have a disagreement with this weighted average method and that it way overestimates the uncertainty--see notes on rough draft page.
To judge the merits of using this technique to measure the radiation rates of other sources, the nature of a different type of radiation had to be determined. From the data collected for the cobalt and cesium samples, it is clear that they generally follow a Poisson distribution, spreading out and moving to greater values as the dwell time increased. From the data, it is also clear that the square root of the average and the standard deviation of the data never exceeds 3.5 %, quantitatively supporting the Poisson distribution. Armed with this knowledge, the same technique used to determine the rate for the background was used to get the rate for the samples. After subtracting the background radiation rate, this gave a value of 560 ± 10 and 1400 ± 40 radiations per second for cobalt-60 and cesium-137 respectively. The value for cobalt is twenty three time higher than the background, while it is nearly sixty times greater for cesium. Clearly the samples are much more radioactive than the surroundings.
Conclusions
For this paper, the radiation rates were measured for varying time intervals to determine its behavior and find a mathematical representation of it. Because the behavior in the probability distributions followed a pattern where the mean grew as the interval increased and the experimental standard deviation grew as the square root of the mean, it became clear that the Poisson distribution is the best way to model the behavior of the background radiation. The difference between an ideal Poisson distribution and the data was found to never vary more than 1.3 % for all the data. Prompted by this, the average rate of radiation per second was calculated from the data. This gave an average rate of 30 ± 4 radiations per second. These values were checked experimentally, giving a value of 30 ± 6 radiations per second, showing that the model was acceptable and could create accurate predictions. The utility of this models is found for any process that, like background radiation, occurs at random independent times, but a definitive average rate. The methods presented here can be used to predict the behavior of these processes to gain very accurate results.
The method could also be used to determine the radiation rates of radioactive samples, and how they compare to the background. By subtracting off the background radiation, it was determined that a small sample of cobalt-60 radiated, on average, 560 ± 24 times a second, approximately twenty three times more often than the background. Also, a sample of cesium-137 was measured to radiate 1400 ± 40 times per second, nearly sixty times more often than the background radiation, and two and a half times more often than the cobalt sample. These measurements illustrate the greater diversity of phenomena that could be described with the Poisson distribution, with great accuracy.SJK 21:22, 14 December 2010 (EST)

technically, your sources are emitting in all directions, and your detector may catch a wider swath of cosmic rays--so the comparison could be a little trickier. But I love that you set out to use real sources!
Acknowledgments
I want to make a couple of acknowledgements of the people that helped me with this report. As always, I want to thank my fellow experimenter, Kirstin Harriger, for all of her help, and doing the experiment. I also want to thank another student, Dan Wilkinson, for originally suggesting that we looked at a radioactive source, and working with Kirstin and I during "extra data week". The professor for this course, Dr. Steve Koch, and the TA, Katie Richardson were both very helpful as well. Outside of our class, I want to thank the original instructor of this course, Dr. Michael Gold, for writing the lab manual, Dr. Stephen Boyd for helping me with my MATLAB code (as always), and Bill Miller for supplying us with the radiation sources.
References
- Poisson, Siméon Denis Recherches sur la probabilité des jugements en matière criminelle et en matière civile (1838) Link here (in French).
- Taylor, John R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements 2e (1997) pg. 174-5 for weighted average 245- 260 for Poisson, Amazon link
- Giuffre, C., Hinow, P., Vogal, R., Strickler, J.R. The ciliate Paramecium shows higher motility in non-uniform chemical landscapes' PLoS ONE, 2010 preprint
- Thorne, M.C. Background radiation: natural and man-made 2003 J. Radiol. Prot. 23 29 link on IOP Science
- United States Environmental Protection Agency Radiation Protection: Cobalt government website link to EPA webpage
- National Library of Medicine: Hazardous Substance Database Cesium, Radioactive government website link to toxnet webpage
- Gold, Michael Physics 307L: Junior Lab Manual (2006) link here
- Wikipedia Poisson Distribution article form the web, external link