Physics307L:People/Gleicher/c
Summary
In this experiment, I will determine the speed of light by measuring the time-of-flight of an optical pulse. The light pulse is emitted from an LED controlled by a pulsing circuit. A signal is sent out from the pulser when the optical pulse is emitted.
The optical pulse is detected by a PMT, which is a very sensitive optical detector.
A signal from the PMT and the LED pulser are both fed into a TAC (time-amplitude-converter) which converts the temporal spread between the signals into a pulse, the amplitude of which is proportional to the temporal spread.
Procedure
The LED is placed at an arbitrary position with respect to the PMT to start. The signal from both the LED and PMT are sent to the TAC after an appropriate delay to make sure the temporal seperation between pulses outputs a reasonable amplitude from the TAC.
To overcome the phenomenon of "time-walk", the amplitude of the output from the PMT is varied using two polarizers.
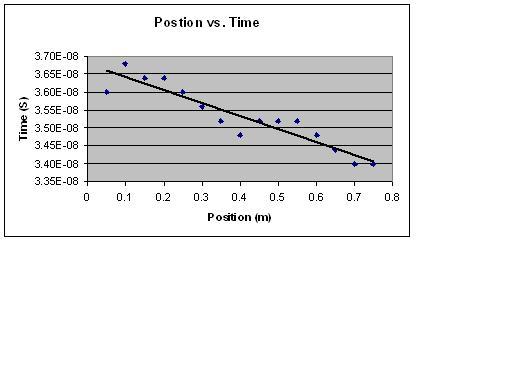
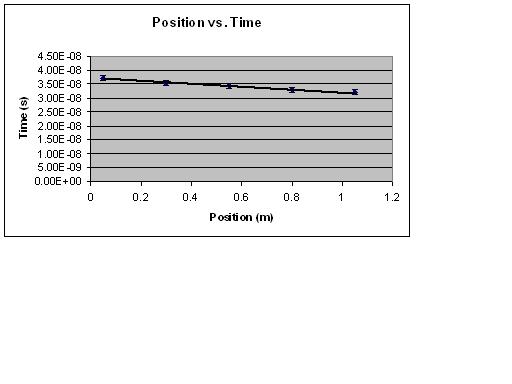
As the distance from the PMT to the LED is varied, the time of flight is measured for each position. When the position vs. time is plotted the value of c can be extracted from a least squares fit.
Data
The raw data can be found here:
Physics307L:People/Gleicher/Notebook/071105
Data Analysis
The data was analyzed using Microsoft Excel's linest function. The value of c and the stDev is given.
Results
My value for the speed of light when the distance is changed in small increments (5 cm ) is (2.41E+08 +/- 2.61E+07)m/s.
The slope is negative but it does not matter as I am using the absolute value.SJK 01:40, 5 December 2007 (CST)

I think that's true, but wouldn't it look at lot better if you had a positive slope? How would you transform the data to do so?
When I plotted the position vs. time for larger increments (25 cm), the value of c is found to be (1.91E+08 +/-1.69E+07)m/s
Conclusion
My two calculated values for the speed of light are:
(2.41 +/- .261)E+8 m/s and (1.91 +/- .169)E+8 m/s. The accepted value for the speed of light is approximately 3E+8 m/s. The accepted value is outside my level of uncertainty, due to systematic error involved in keeping the voltage on the PMT constant, along with my random error. The voltage on the PMT is difficult to keep constant as it is set graphically using an osilloscope.
The value for c corresponding to the small incremental increase is a better value as it includes many more data points.SJK 01:41, 5 December 2007 (CST)

But what is the accepted value? Is the accepted value within your level of uncertainty? Do you have systematic error beyond your random error?