Physics307L:People/Gibson/Formal Lab Report 2
- MEASURING THE SPEED OF LIGHT BY A TIME DELAYED SIGNAL BETWEEN A LIGHT EMITTING DIODE AND PHOTOMULTIPLIER TUBE
Author: Zane Gibson
Experimentalists: Zane Gibson Matthew Gooden,
Department of Physics and Astronomy
University of New Mexico
Albuquerque, NM
Abstract
This experiment was done to determine the value of [math]\displaystyle{ c }[/math] or the value of the speed of light. To complete this experiment, a time amplitude converter (TAC) and an oscilloscope were used to measure the time between a light signal from an light emitting diode (LED) and a photo multiplier tube (PMT). By changing the distance between the PMT and the LED, we were able to record various voltages for various distances, then we converted the voltage to a time and constructed a trend line of our distances and times using a least squares fit analysis. The slope of this trend line was the constant we were originally looking for, the speed of light. For this experiment we found our constant to be [math]\displaystyle{ c=\left(2.892 \pm .077\right)\times10^8 m/s }[/math] which is very close to the theoretical approximation of [math]\displaystyle{ 2.99\times10^8 {m/s} }[/math].
Introduction
The speed of light has been used in many branches of physics in many different ways. The speed of light was first seen as constant by Albert Einstein and as such is a basis for the branch of physics known as special realitivity [1] As such, this value has been disputed and many experiments have been performed to find this value. The first accurate way to find the value was done around 1960 where lasers first started to become used widely in optical physics. It wasn't until 1972, when the National Institute of Standards and Technology employed the developing laser technology to measure the speed of light at 299,792,458 meters per second [2]. Since then, the speed of light has been used in a variety of applications from optical physics to biomedical physics, more specifically using light to shrink cancer cells [3]. In this experiment we consider how close we can approach the value of [math]\displaystyle{ c }[/math], while minimizing our error and uncertainty in our measurements.
Methods and Materials
Equipment List
1.Time-Amplitude Converter (TAC) - EG&G Ortec Model 567 TAC/SCA
2.Light Emitting Diode
3.Photomultiplier Tube (PMT) - Magnetic Shield Co., 22P50
4.DC Power supply (LED) - Harrison Laboratories, Model 6207A 0-160V,0-.2A
5.DC Power supply (PMT)- Bertan Associates,Inc. Model 315, DC Power Supply 0-5000V,0-5mA
6.Oscilloscope - Tektronix TDS 1002 2 Channel Digital Storage Oscill., 60MHz 1GS/s
7.BNC Connector Cables - 6
8.Delay box - Canberra NSEC Delay Box, Model 2058
9.Several Meter Sticks - 4
10.Long Tube (cardboard or other nontransparent material) - 4 meters long
-
Photo 1:Center is a storage rack for several pieces of equip. From left: power supply for photomultiplier-Item 5, delay box-Item 7, TAC (time amplitude converter)-Item 1
-
Photo 2:Small gray box center of the photo is the Power supply used for LED light emitter. Item 4 from equip. list
-
Photo 3:Oscilloscope. Item 6.
-
Photo 4:On top tried different time delay to try and get better signal.
Procedure
Set up - To begin the experiment we first collected all our equipment, then proceeded to first get power to the LED. We then did the same for the PMT (NOTE: Do not expose the PMT to massive quantities of light while operating, this can destroy the PMT) then placed them in the long cardboard tube. We then bolted the LED to one of the ends of a meter stick (so we could vary the distance) and taped the sticks end to end to allow us plenty of variable distances. Using a connector cable, we connected the PMT signal output into channel 1 of the oscilloscope and plugged the response from the LED (when it sent a signal) to the TAC. We then ran a cable from the TAC to the time delay box, and then to channel 2 of the oscilloscope. The distance of how far in or out the LED was is arbitrary. Taking whatever place as the zero works fine and recording the differences in the distances is what is important.
Collection- To begin we left the delay box set to zero delay for the experiment, as none was ever needed. We then adjusted the voltage knob on the PMT power source so that the PMT was receiving a voltage of approximately 1900 volts (as per recommendation from last years lab manual [4]. Then we adjusted the LED power supply to approximately 200 volts. Then turning to the oscilloscope we saw two signals present on the screen, one from the PMT and the other from the TAC. The PMT signal was characterized by a sharp downward voltage drop, while the TAC signal was characterized by a rapidly oscillating square wave. Using the acquire button on the oscilloscope we chose to average over the values that the oscilloscope is receiving to allow measurements to be taken must easier, rather than constantly adjust the equipment to find a steady value. We chose the 128 setting under the average command, to greatly stabilize the signal we were viewing. At this point we began our data collection, having one of us at the other end of the tube to move the LED, and the other at the end with the PMT and other equipment. We picked a value of the voltage on Ch 1 and attempted to maintain that value for the duration of the measurements made for each data set, this is need because as the LED is moved toward or away from the PMT the intensity of the signal changes and by aligning or unaligning the polarizers we were able to keep the signal constant. This was accomplished by turning the PMT left/right to align or unalign its polarizer with that of the LED. Taking care to note our chosen zero mark, we then moved the LED away from the PMT a short distance, recording this change in distance, while holding the PMT steady. For this experiment, we are not concerned with the actual distance between the PMT and LED. Rather at any particular distance between the PMT and LED we make a measurement and then we are only concerned with the change in that distance for the next measurement, since we are measuring the time delay of the signal from the LED pulse and the PMT signal. Once the LED was moved the PMT was adjusted to regain the chosen voltage, and then using the measure function to allow us to see the values outputted to channels 1 and 2, we recorded the voltage output from the TAC. To complete the particular data set we made several more measurements in the same fashion always recording the change in distance from the original zero mark. Every data set has different settings for voltages we were aiming for from the PMT, as listed below in the results and discussions.
Analyzing- In our analysis we used two programs to construct graphs and do averages/ standard deviations for our results. These programs were Microsoft Excel and Mathworks Matlab.
Results and Discussion
Below are the 4 data sets we took and a discussion of each set. In discovering the times for each data set, we were required (since we didn't measure time) to use the equation V=G*T where V is voltage; T is the time we want, and G is a constant set before we began taking measurements = 1/10 volt/nanosecond.
Here we took down measurements as listed in the procedure and placed them below:
Table 1
| Data Set 1 Measurments | PMT Ch1 Voltage | TAC Time delay voltage | Distance (cm) | Time (ns) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.24\pm.04 }[/math] | 60 | 32.4 |
| 2 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.2 \pm.04 }[/math] | 80 | 32 |
| 3 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.08 \pm.04 }[/math] | 100 | 30.8 |
| 4 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.00 \pm.04 }[/math] | 120 | 30 |
| 5 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.96\pm.04 }[/math] | 140 | 29.6 |
| 6 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.00 \pm.04 }[/math] | 130 | 30 |
| 7 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.12 \pm.04 }[/math] | 90 | 31.2 |
| 8 | [math]\displaystyle{ 600 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.2 \pm.04 }[/math] | 70 | 32 |
Table 1 shows a constant for the speed of light being around [math]\displaystyle{ c=\left(2.68 \pm 0.18\right)\times10^{8} m/s }[/math] given all the settings labeled above.
Table 2
| Data Set 2 Measurments | PMT Ch1 Voltage | TAC Time delay voltage | Distance (cm) | Time (ns) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.44\pm.04 }[/math] | 70 | 24.4 |
| 2 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.4 \pm.04 }[/math] | 80 | 24 |
| 3 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.36 \pm.04 }[/math] | 90 | 23.6 |
| 4 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.32 \pm.04 }[/math] | 100 | 23.2 |
| 5 | [math]\displaystyle{ 800 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.32\pm.04 }[/math] | 110 | 23.2 |
Table 2 shows a speed of light being [math]\displaystyle{ c=\left(2.94 \pm 0.42\right)\times10^{8} m/s }[/math] given all the settings labeled in the table above.
Table 3
| Data Set 3 Measurments | PMT Ch1 Voltage | TAC Time delay voltage | Distance (cm) | Time (ns) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.8\pm.04 }[/math] | 27.5 | 28 |
| 2 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.64 \pm.04 }[/math] | 70 | 26.4 |
| 3 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.52 \pm.04 }[/math] | 110 | 25.2 |
| 4 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.44 \pm.04 }[/math] | 130 | 24.4 |
| 5 | [math]\displaystyle{ 720 \pm 8 {mV} }[/math] | [math]\displaystyle{ 2.72\pm.04 }[/math] | 50 | 27.2 |
Table 3 shows a speed of light being [math]\displaystyle{ c=\left(2.89 \pm 0.08\right)\times10^{8} m/s }[/math] given all the settings labeled above.
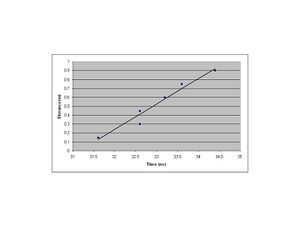
- NOTE: Table 4 was analyzed separately from the other data sets. This was because the delay box was used to help improve our accuracy of getting to the theoretical value of the speed of light, as discussed in the conclusions.
Table 4
| Data Set 2 Measurments | PMT Ch1 Voltage | TAC Time delay voltage | Distance (cm) | Time (ns) |
|---|---|---|---|---|
| 1 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.16\pm.02 }[/math] | 15 | 31.6 |
| 2 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.26 \pm.02 }[/math] | 30 | 32.6 |
| 3 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.26 \pm.02 }[/math] | 45 | 32.6 |
| 4 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.32 \pm.02 }[/math] | 60 | 33.2 |
| 5 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.36\pm.02 }[/math] | 75 | 33.6 |
| 6 | [math]\displaystyle{ 640 \pm 8 {mV} }[/math] | [math]\displaystyle{ 3.44\pm.02 }[/math] | 90 | 34.4 |
Table 4 shows a value of [math]\displaystyle{ c=\left(2.85 \pm 0.03\right)\times10^{8} m/s }[/math] given a delay of 2 nanosecs and all labeled settings above.
- NOTE: See acknowledgments section
Once we completed calculating our times for each of the trials, we then proceeded to construct 3 least squares plots to determine what our value of the speed of light would be. To do this we simply took the distance recorded vs time which then gave us a very linear graph... the slope of this line is the constant we were looking for.
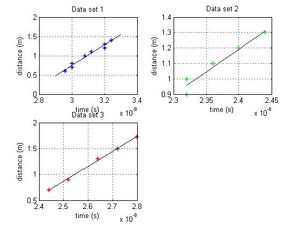
- The slopes for each data set are listed below:
Data Set 1
[math]\displaystyle{ c=\left(2.68 \pm 0.18\right)\times10^{8} m/s }[/math]
Data Set 2
[math]\displaystyle{ c=\left(2.94 \pm 0.42\right)\times10^{8} m/s }[/math]
Data Set 3
[math]\displaystyle{ c=\left(2.89 \pm 0.08\right)\times10^{8} m/s }[/math]
Average of all three data sets:
[math]\displaystyle{ c=\left(2.83 \pm .23\right)\times10^8 m/s }[/math]
From here we calculated our relative error to determine the amount off of the theoretical value:
[math]\displaystyle{ Relative Error=\frac{\left|2.83\times10^{8}-2.99\times^{8}\right|}{\left|2.99\times10^{8}\right|}=0.0535=5.3% }[/math]
Possible sources of uncertainties have to do with the equipment. We ran the same experiment several times over the same values to see how close our values would be to one another after several repeated measurements. We found quite a discrepancy and we've concluded it has to do with some sort of systematic error which we are unable to account for at this time.
Conclusions
Thus our closest approach to the theoretical value of the speed of light is [math]\displaystyle{ c=\left(2.892 \pm .077\right)\times10^8 m/s }[/math]. This is a good value to receive especially with our unfamiliarity with most of the equipment. Additional error analysis shows our reported value we find having a relative error given by [math]\displaystyle{ RE=\frac{\left|2.99\times10^{8}-c\right|}{\left|2.99\times10^{8}\right|}=0.0328=3.3% }[/math] which is again very good considering the time to take measurements was somewhat constrained. With data set 4 we attempted to improve on this error by taking more measurements and possibly shrinking this value. The ideas used are explained next to the table above but as can be seen from the data set none of these things were able to improve the results, and actually left us with a value of c that is farther off than either of data sets 2 or 3. The data given above for set 4 is the first and more accurate attempt made for that set in comparison to the other trials. It must be concluded that there is some form of systematic error in the experiment that is not being accounted for and at this time with our little knowledge of the inner workings of the electronics we cannot specifically pin point the problem. Our most accurate and reported value is [math]\displaystyle{ c=\left(2.892 \pm .077\right)\times10^8 m/s }[/math].
Acknowledgments/References
1. [Special Relativity]
2. [Measuring the Speed of Light] as done by NIST.
3. [Cancer] article and using light to shrink cells
4. [Previous Course lab manual] from Dr. Gold
I would like to thank Dr. Steve Koch for help with theory, instrumentation and experiment design.
I would also like to thank my lab partner Matt Gooden for his help in presentation of the data.