Physics307L:People/Cochran/Poisson distribution
Steve Koch 22:51, 21 December 2010 (EST):It is nice data and histogram analysis. However, I don't see you compare to the theoretical Poisson distribution, nor investigate how the standard deviation behaves relative to the mean.
Summary
In this lab, we investigated the Poisson distribution using atmospheric muons and a scintillator-PMT. The Poisson distribution describes a set of events that occur randomly, but with an average rate. My lab notebook for this lab is visible here, and Cristhian Carrillo was my partner for this lab.
Procedure/Results

We collected data measuring the incidence of radioactive events at various dwell times, found the average values for each set and its standard deviation, and graphed the frequency of the number of counts per channel vs. the number of counts per channel, using MATLAB and Excel. We used a scintillator/PMT, a computer, and UCS30 software. The results are below.
Conclusion
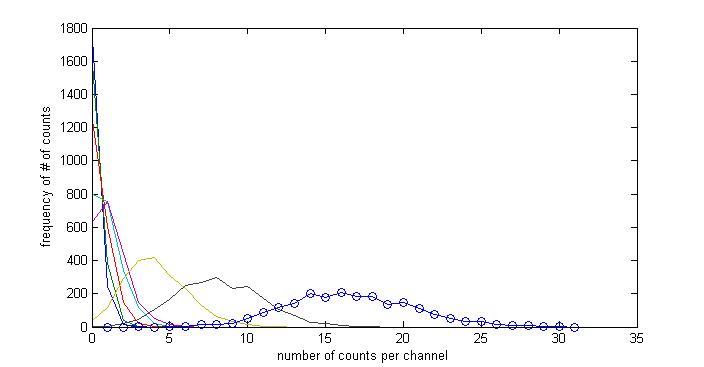
This image shows the all the separate dwell times graphed together, showing that the peak of the distribution shifts to the right as dwell time is increased. The distribution also becomes wider with increased dwell time.