Paul Magnano:Assignment Week 2
From OpenWetWare
Jump to navigationJump to search
Assignment week 2
Question 1
- consider the model:
dcdt = q*u - q*c -((y*c)/(K+c));
dydt = (y*r*c)/(K+c) - q*y
- variables
- q*u= inflow rate
- q*c=outflow rate
- r=net rate of yeast population growth
- y=yeast population
- c=nutrient concentration
- k=constant
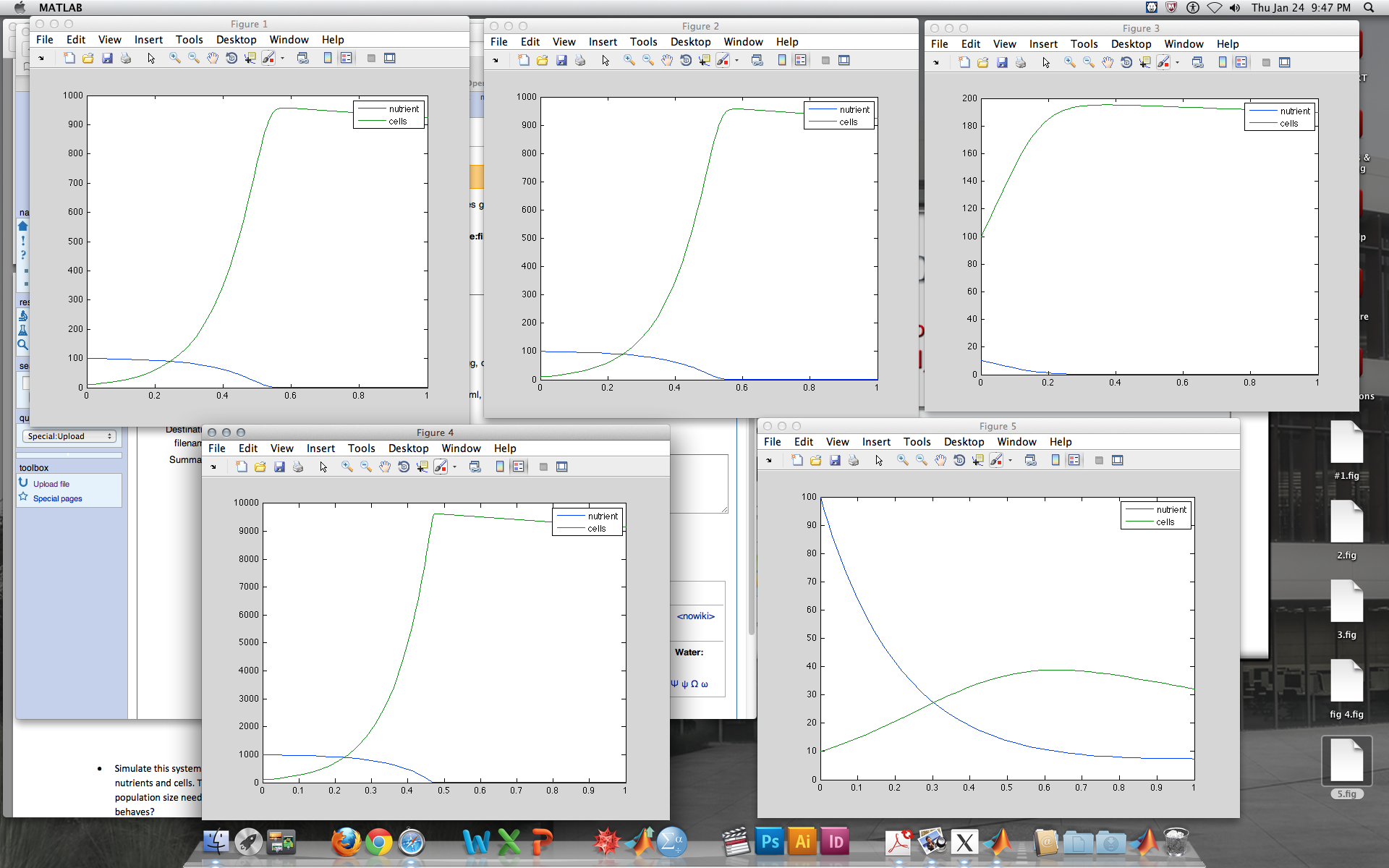
- First I started a simulation with a nutrient concentration of 100, a starting population of 10, q at 0.1, and u,r & K at 10. This resulted in a gradual decline in nutrient which eventually reached 0 and exponential cell growth that leveled off when nutrient levels reached zero. This is illustrated by fig. 1. Next I ran the same simulation but changed starting population to 100 and nutrient concentration to 10, this resulted in the same effects in growth, and is illustrated by fig. 2. Next I ran the same simulation but made initial cell population 100 and initial nutrient concentration 1000, and again the same results occurred in terms of graph shape, and this is illustrated by fig. 3. Next I ran a simulation with a nutrient concentration of 100, a starting population of 10, q at 10, and u,r & K at 10. This resulted in both cell population and nutrient concentration declining, with cell pop. reaching zero and nutrient concentration leveling out. This is illustrated by fig 4.Next I ran a simulation with a nutrient concentration of 100, a starting population of 10, q at 5, and u,r & K at 10. in this case both nutrient concentration and cell pop. reached stable levels where neither approached zero. This is illustrated in fig 5. Overall I would say the system tends to produce high rates of cell growth when nutrients are sparse, cell decline when nutrients are overabundant, and stability of population growth (sustainable) when nutrient concentration is in sufficient.
Question 2
- simulate this model:
dcdt = q*u - q*c -((y*c)/(K+c));
dydt = (y*r)*(1-(y/(M*c)));
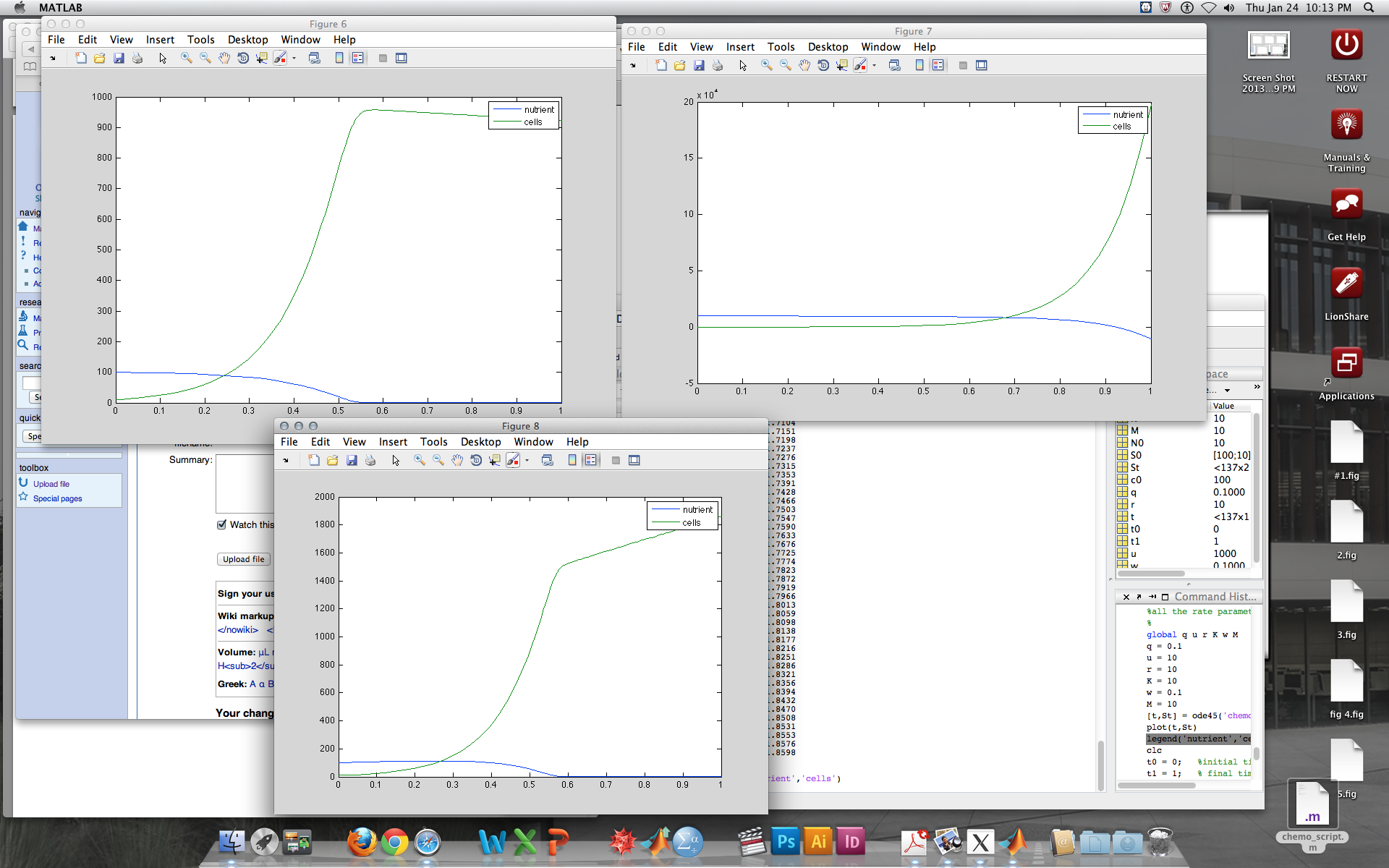
- First I ran the simulation with the values 0.1 for q& w, u, r, k, & M with values of 10, an initial population of 10 and a starting nutrient concentration of 10. The graph ended up showing exponential cell growth and nutrient concentration approaching zero as illustrated in fig. 6. Next I ran the simulation with the values 0.1 for q& w, u, r, k, & M with values of 10, an initial population of 10 and a starting nutrient concentration of 10000. This resulted in overall decreasing nutrient concentration after a lag period, as well as exponential cell growth after a corresponding lag period, as illustrated in fig 7. Finally, I ran the simulation with the values 0.1 for q& w, r, k, & M with values of 10, u with a value of 1000 an initial population of 10 and a starting nutrient concentration of 10. This produced rapid cell growth and rapidly dropping levels of nutrient concentration, as illustrated in fig 8.This system seemed to behave similarly to the previous system modeled, except that the cells growth is limited by the carrying capacity, as they can only grow as fast as it allows the population to.
- I think it would be interesting to model this while accounting for the yeasts production of one of its waste products in fermentation, alcohol. Since The waste of its life cycle can end up killing it it would be interesting to see how this effects the yeasts population growth in a chemostat. Theoretically the graph of waste vs cell pop. would could look like a wave function, with yeast population rising and fall in sync with the rise and fall of waste concentration.