Physics307L:People/Gooden/Notebook/070917
From OpenWetWare
(Redirected from Matthew E. Gooden Lab book/070917)
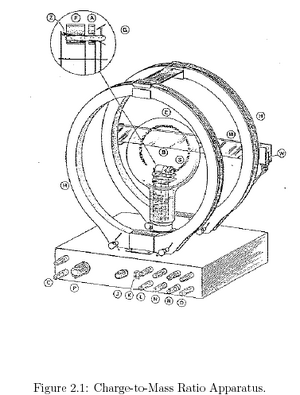
e/m Ratio Experiment
SJK 00:22, 18 October 2007 (CDT)

Very nice description!
- This experiment is using the Helmholtz coils and a helium filled tube with an electron gun to measure the e/m ratio. That is the electron charge-to-mass ratio. A heating element inside the tube is heated to the point where electrons in the metal are 'boiled' off and with the help of a voltage applied between two plates the electrons are accelerated. The helmholtz coils are supplied with a current to generate a magnetic field that according to the Lorentz force law will cause the electrons path to be bent into a circular trajectory inside of the tube. As the electrons move through the tube they collide with helium atoms that become excited by the collision and then radiate, allowing us the see the path that the electrons are taking. Measuring the radius of the electrons circular path allows for the calculation of the Charge-to-Mass ratio.
Procedure
Materials
This experiment requires 2 DC power supplies, 2 digital volt meters, 1 helmholtz coil, 1 vacuum tube/electron gun assymbly, and 1 high voltage supply.
Set Up
step 1 - Connect one of the DC power supplies in series with a DVM, that will measure
current, to the Helmholtz coil jacks on the bottom left side of the apparatus.
step 2 - Connect the other DC power supply to the electron gun heater jack on the front
right of the apparatus.
step 3 - Connect the high voltage power supply to the electron gun electrode jacks that are
next to the heater jacks.
step 4 - Finally connect the second DVM to the voltmeter jacks on the apparatus to measure
accelerating voltage.
- Complete Set Up
Step 1 - Once all of the equipment is connected, turn on the power supply to the heater
jacks and allow the electron gun to heat up for several minuets.Keep the voltage
under 6.3 volts.
Step 2 - Once the electron gun has heated for several minuets go ahead and turn on the high
voltage supply to around 250 volts(for best results) and begin to increase the
current through the coils using the current knob on the apparatus. Also, turn on
both DVM's to being measuring voltage and current through the coils.
DATA
SJK 00:25, 18 October 2007 (CDT)

Nice recording of the data. It would also be good to record your measurement uncertainties for the various measurements. For example, "all radius measurements +/- 0.1 cm"
- DATA SET 1 at constant voltage - V=270 V
Measurment 1 Measurment 6
I=1.04 I=.99
r1=5.4cm,r2=4.1cm r1=5.5cm,r2=4.1cm
* r=4.5cm *r=4.55cm
Measurment 2 Measurment 7
I=1.01 I=1.22
r1=5.5cm,r2=4.1cm r1=4.9cm,r2=3.9cm
*r=4.5cm *r=4.35cm
Measurment 3 Measurment 8
I=.95 I=1.13
r1=5.6cm,r2=4cm r1=5.2cm,r2=4cm
*r=4.6cm *r=4.2cm
Measurment 4 Measurment 9
I=1.18 I=1.08
r1=5cm,r2=4cm r1=5.3cm,r2=4.1cm
*r=4.25cm *r=4.3cm
Measurment 5 Measurment 10
I=1.24 I=1.30
r1=4.8cm,r2=3.9cm r1=4.6cm,r2=3.9cm
*r=4cm *r=3.65cm
- DATA SET 2 at constant current - I=1.35 A
Measurment 1 Measurment 6
V=270 V=320
r1=4.4cm,r2=4cm r1=4.8cm,r2=3.9cm
* r=3.7cm *r=4.15cm
Measurment 2 Measurment 7
V=289 V=330
r1=4.6cm,r2=4cm r1=4.9cm,r2=4.1cm
*r=3.9cm *r=4.25cm
Measurment 3 Measurment 8
V=298 V=348
r1=4.6cm,r2=4cm r1=5cm,r2=4.2cm
*r=3.95cm *r=4.35cm
Measurment 4 Measurment 9
V=307 V=360
r1=4.6cm,r2=4cm r1=5cm,r2=4.2cm
*r=4cm *r=4.45cm
Measurment 5 Measurment 10
V=313 V=388
r1=4.7cm,r2=4cm r1=5.1cm,r2=4.3cm
*r=4.1cm *r=4.55cm
- DATA SET 3 for random values of current and voltage
Measurment 1 Measurment 6
V=180,I=1.21 V=220,I=1.30
r1=3.9cm,r2=3.5cm r1=4.1cm,r2=3.6cm
* r=3.7cm *r=3.85cm
Measurment 2 Measurment 7
V=189,I=1.02 V=230,I=1.33
r1=4.7cm,r2=3.6cm r1=4.2cm,r2=3.7cm
*r=4.15cm *r=3.85cm
Measurment 3 Measurment 8
V=198,I=1.09 V=248,I=1.14
r1=4.6cm,r2=3.7cm r1=5cm,r2=4cm
*r=4.15cm *r=4.5cm
Measurment 4 Measurment 9
V=207,I=1.18 V=260,I=1.01
r1=4.4cm,r2=3.8cm r1=5.5cm,r2=4.1cm
*r=4.1cm *r=4.8cm
Measurment 5 Measurment 10
V=212,I=1.25 V=288,I=4.33
r1=4.2cm,r2=3.7cm r1=4.6cm,r2=4cm
*r=3.95cm *r=4.3cm
ANALYSIS
- With the three data sets, we used the formula on the e/m apparatus to calculate e/m for each
measurment and then found the mean for the set and the standard deviation.
SJK 00:26, 18 October 2007 (CDT)

I don't think this formula is correct
[math]\displaystyle{ e/m=\frac{2V}{(B*I)^2R^2} }[/math]
- Value of e/m for data set 1
e/m = 6.28343E+11 +/- .725E+11
(Koch says (6.3 +/- 0.7)*10^11)
- Value of e/m for data set 2
e/m = 3.39E+11 +/- .0272E+11
(3.39 +/- .03)*10^11
- Value of e/m for data set 3
e/m = 3.07111E+11 +/- .00840E+11
(3.07 +/- .01)*10^11
Data Analysis of set 1 and random set
SJK 00:28, 18 October 2007 (CDT)

This is a good start to a discussion of the errors...but I don't think you fully explained everything that we had talked about. Also, it would be good to include graphs as images to show how the e/m "constant" varies with current, like we saw.
- These values are all very far off from the accepted value of the charge-to-mass ratio of
e/m = 1.76e+11 coulomb/kg. Our result from our first data set is grossly inaccurate and the other two results while not as bad are still not very good. We believe that we are experiencing systematic errors in the experiment, that are most likely not human caused since the another group who performed this experiment obtained results very near ours.
- Errors that could be apart of the experiment include:faulty DVM's, or faulty e/m tube. Other
pausible sources of error could be that the equation used to calculate the ratio is incorrect and also that the constant B (magnetic flux density) for the helmholtz coils is inaccurate.