LuisM SPi
Graphical Stochastic π Calculus model for iGEM Mexico 2007 Oscillator
The motivation for use Stochastic π Calculus for modeling our constructions is based in the advantages that present this formal lenguage against the ordinary differential equations (ODE's). There are many papers that describe this advantages, escentially I used it because is a different approach to model biological systems, a very interesting approach!.
I have learned SPi alone without any supervision, and my models has not to be necessary corrects.
This is the representation with logic gates
Basically in the repressilator we can found three logical gates with negative control. Our construction consist by three negative gates and two positive gates.
The characteristics of the construction are as follows:
1.We have a X Constitutive gene that inhibits LasR and LuxpR genes.
2.Lambda cl is then opened and begin producing the autoinductor protein that switch promotes LuxpR.
3.When LasR is unblock, it starts parallel production of two proteins, GFP and the protein that activates LuxpR.
4.LuxpR gets unblock and produce at the same time RFP and the inhibitor of the lambda cl gene.
5.When lambda cl get blocked it won't produce anymore the protein that activates LasR.
6.As the gene LasR is blocked, GFP stops and the production of the protein that unblock LuxpR stops.
7.Then LuxpR won't produce RFP and the inhibitor of lambda cl stops producing.
8.When the inhibitor of lamda cl degrades the cycle is finished and we returned to the original state.
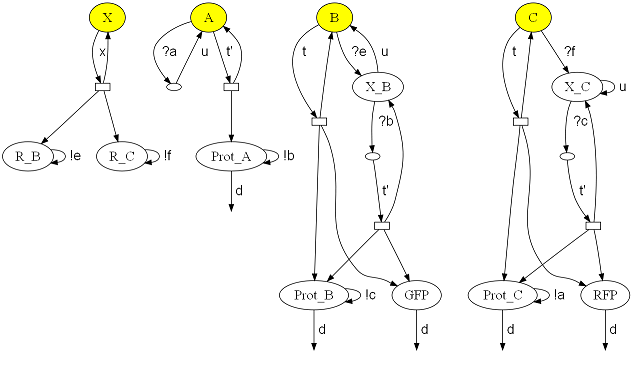
Now the model in Graphical Stochastic π Calculus Representation
g(a,b)= ?a.g'(a,b) + Ʈt'.(P(b)|g(a,b))
g'(a.b)= Ʈu . g(a,b)
P(b)= !b . P(b) + Ʈd
g(b,c)= ?e . g'(b,c) + Ʈt . (P(c)|GFP()|g(b,c))
g'(b,c)= Ʈu . g(b,c) + ?b . g(b,c)
g(b,c)= Ʈt' . (P(c)|GFP()|g'(b,c))
P(c)= !c . P(c) + Ʈd
GFP()= Ʈd
g(c,a)= ?f . g'(c,a) + Ʈt . (P(a)|RFP()|g(c,a))
g'(c,a)= Ʈu . (P(a)) + ?c . g(c,a)
g(c,a)= Ʈt' . (P(a)|RFP()|g'(c,a))
P(a)= !a . P(a) + Ʈd
RFP()= Ʈd
X(e,f)= Ʈx . (P(e)|P(f)|X())
P(e)= !e . P(e) + Ʈd
P(f)= !f . P(f) + Ʈd
Once i had the model, i simulated it in the Stochastic Pi Machine(Phillips, et all)
This is the code that I wrote for the SPiM.
directive sample 10000.0 1000
directive plot !b;!c;!a
val x = 1.0
val t = 0.001
val t'= 1.0
val d = 0.001
val u = 0.0001
val bind = 1.0
new a@bind:chan
new b@bind:chan
new c@bind:chan
new e@bind:chan
new f@bind:chan
let X()= delay@x;(XB()|XC()|X())
and XB()= !e; XB()
and XC()= !f; XC()
let A()= do ?a;delay@u;A() or delay@t';(Prot_A()|A())
and Prot_A()= do !b;Prot_A() or delay@d
let B()= do ?e;(X_B()) or delay@t; (Prot_B()|GFP()|B())
and X_B() = do delay@u; (B()) or ?b; delay@t'; (Prot_B()|GFP()|B())
and Prot_B()= do !c;Prot_B() or delay@d
and GFP()= delay@d
let C()= do ?f; X_C() or delay@t; (Prot_C()|RFP()|C())
and X_C()= do delay@u; X_C() or ?c; delay@t'; (Prot_C()|RFP()|C())
and Prot_C()= do !a;Prot_C() or delay@d
and RFP()= delay@d
run(X()|A()|B()|C())