Koch Lab:Publications/Drafts/Magnetic Microtubule Steering/Paper
Title
Electromagnetic Manipulation of Microtubule Shuttles End-Labeled with Magnetic Beads
Authors
Amanda M. Trent1,2, Steven J. Koch1,3, George D. Bachand1, and Gayle E. Thayer1
1Sandia National Labs, NM
2Current affiliation: University of California-Santa Barbara
3Current affiliation: University of New Mexico
Abstract
Using an electromagnet mounted on an optical microscope, we can affect the direction and speed of functionalized microtubules (MTs) powered by kinesin motor proteins in an inverted motility assay. Magnetic beads were selectively attached to the leading end of MTs, allowing for electromagnetic manipulation of the MTs when the assay flow cell is placed between the poles of the magnet. The position of the attached bead was monitored optically while the electromagnet current was dynamically adjusted to apply calibrated forces. We present data showing a moving bead repeatedly changing direction by approximately 50° to align with a cycled force of 0.7 pN, and another bead slowing by roughly 50% when traveling against a 2 pN force. This study lays the groundwork for future devices using magnetic field gradients to steer microtubule shuttles and for future experiments measuring force-velocity relationships of a collection of kinesin motor proteins within motility assays.
Introduction
The kinesin-microtubule transport system has been proposed for use in powering microfluidic devices [1]. Integrating kinesin motor proteins and microtubule (MT) shuttles as mechanical components in such devices could provide a means to program or regulate processes such as materials synthesis or chemical recognition at a molecular level. In addition, using this system to actively transport nano-particles in microfluidic environments would eliminate destructive friction and heat generation typically seen in devices relying on fluid pumping or electric fields [2]. With promising applications of this nanoscale machinery, recent work has focused on enhanced control and manipulation of this nano-bio system [3]. One possible strategy is to use microfabricated magnetics to guide the direction of transport. Here we propose to first use a macroscopic magnetic testbed (Figure 1a) to quantitatively define the parameters required for a device incorporating microscopic magnetics. Furthermore, this testbed can be used to probe general biophysical properties of the kinesin-MT system such as the stall force of a MT as a function of kinesin motor density.
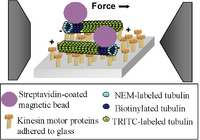
We have developed a method to laterally direct MTs within inverted motility assays (IMAs) [4] using an adjustable and calibrated magnetic field gradient. To magnetically manipulate the MTs, we attached single magnetic beads to the leading end of MTs via a streptavidin-biotin linkage. As the leading end of a MT ratchets side-to-side “searching” for the next motor protein to bind to in the IMA, an electromagnetic force acting on the bead attached to this leading end can effectively bias the direction of the MT. To generate these forces and simultaneously track the motion of the beads/MTs, we constructed a computer-controlled electromagnet (EM) incorporated into an upright optical microscope. Specialized flow cells and a long working distance objective allowed positioning of the electromagnet pole close enough to the sample to apply piconewton-level forces to the beads. With this instrumentation we were able to take multiple measurements of single beads/MTs at one time as the EM field was cycled on and off. The dynamic forces applied to the magnetic beads during each cycle were determined through finite element modeling of the electromagnet field and field gradient combined with known properties of the magnetic beads. In addition, the forces on the microspheres were directly calibrated using microfabricated springs [5].
Methods
Microtubules and Bead Attachment
The Drosophila kinesin used in this study moves only toward the positive end of an MT and therefore, in an inverted motility assay, the minus end of an MT is the leading end. Normal microtubule polymerization occurs from both the positive and negative ends of the MTs [6]. To create MTs with biotinylated tubulin only at the minus end, we first capped the minus end of short, biotinylated MT ‘seeds’ with n-ethylmaleamide (NEM)-labeled tubulin. We were then able to polymerize rhodamine-labeled tubulin strictly in the positive direction off of the seeds. Finally, 2.8µm diameter streptavidin-coated magnetic beads (Dynal M-270) washed and diluted 1:2 in BRB80T (BRB80 [80 mM PIPES, 1 mM MgCl2, 1 mM EGTA], 20 uM Taxol) were combined with the functionalized MTs in motility solution (BRB80T, 0.2 mg/mL casein, 1mM ATP, 20 mM dextrose, 0.02 mg/mL glucose oxidase, 0.08 mg/mL catalase, 1 mM DTT) at ratios ranging from 1:4 to 1:2 (% vol., beads:MTs). The two were combined just prior to use in the IMA to avoid settling and crosslinking of MTs via the beads. The bead:MT ratio was adjusted as needed to maximize the number of MTs with a single bead attached. Figure 1b illustrates the functionalization of the microtubules and subsequent bead attachment.
Adapting methods reported in the literature [7], we labeled tubulin with NEM by adding 1 mM NEM to 6 mg/mL tubulin suspended in GPEM (BRB80, 1mM GTP, 10% glycerol). The reaction sat on ice for 10 minutes before being quenched with 8 mM dithiothriotol (DTT) for a final volume of 90 uL. Excess NEM, GTP and DTT were removed by running the mixture through BioRad P6 spin-columns equilibrated with BRB80. 2 uL aliquots were stored at -80°C.
Biotinylated MT seeds were prepared by polymerizing a mixture of 50% biotinylated/rhodamine-labeled tubulin (5mg/ml total tubulin) in GPEM at 37°C for 20 min., then diluted 100-fold and stabilized with BRB80T. These biotinylated MTs were then sheared by passing through a 30 ½ gauge syringe needle 6-8 times, creating small MT segments or “seeds” (~1 um long). The seed mixture was centrifuged at 30 psi (~165,000 x g) for 5 min. in a Beckman Coulter Airfuge. The supernatant containing excess biotinylated tubulin was removed and discarded and the concentrated seed pellet was resuspended with 20 uL BRB80T. Then, in order, 2 uL (~5mg/ml) NEM-labeled tubulin and 4 uL (5mg/ml) 50% rhodamine-labeled/unlabeled tubulin was added to the seeds. The seed/tubulin mixture was incubated at 37°C for 35 min. and then stabilized with BRB80T (200 uL final volume), yielding fluorescent rhodamine-labeled microtubules with a short biotinylated section on the minus end [8].
The magnetic beads used in this work were streptavidin-coated 2.8 µm diameter polystyrene beads (Dynabeads® M-270 Streptavidin, purchased through the Invitrogen Corp., www.invitrogen.com) with embedded maghemite and magnetite superparamagnetic nanocrystals. Quantification of individual bead characteristics was performed using transmission electron microscopy, and a novel MEMs force sensor technique described in reference [5]. It was determined that the beads are spherical, have uniform diameter, and the magnitude of the magnetic moment,[math]\displaystyle{ m vector }[/math], of individual beads is 2.7 x10-13 A•m2 +/- 9% (see figure 1(d)).
Electromagnet System
An electromagnet (EM) was constructed using a 3/8 inch diameter soft steel rod, one end machined to a conical point with an included angle of 64 degrees and a blunt tip diameter of 2.75 mils and the other end machined to a flat face, heated and bent into a C-shape with a distance of 0.48 inches between the poles. The magnet was wound with 228 turns of 1mm diameter copper wire. The poles of the magnet were shaped so as to yield a maximum magnetic field gradient in the axial-direction and a symmetric minimum in the radial directions, and were spaced to allow a sample to fit between them (Figure 1a). The EM was mounted on an XYZ translation stage, independent of the x-y stage of an upright optical microscope (Olympus BX-51). Decoupling the magnet from the microscope translation stage allowed precise position of the electromagnet relative to the microscope objective, independent of sample movement, effectively allowing us to determine the forces across any field of view based on knowledge of the off-screen magnet position. For the objective lens to view the sample, yet not interfere with the magnetic field or physically hit the pole piece, we used a 50X long working distance objective (Olympus LMPlanFl, w.d. 10.6 mm). Due to spatial constraints, it was necessary to use a flow cell that is smaller than those constructed from standard coverglasses and typically used in IMAs, we used glass Vitrotubes™ (Borosilicate glass Vitrotubes™ purchased from VitroCom, Inc. http://www.vitrocom.com). This setup allowed visualization of the beads being transported within the field of view. However, due to the relatively large amount of glass between sample and objective, we were not easily able to image the microtubules (25 nm diameter filaments) while in the EM setup. While this precludes us from knowing the exact attachment geometry and microtubule lengths and lends some difficulty to interpretation, the data are sufficient for the proof of principle results we report and the problem will be overcome by use of improved flow cells.
Force Calibration
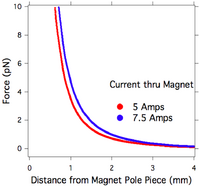
The Dynal 280 beads by the manufacturer’s specifications are 2.8 µm in diameter and 4.8% volume loading of maghemite nanocrystals with an effective initial susceptibility of 21 and saturation magnetization per unit volume of 419,000 A/m. As described in reference 5, using a microelectromechanical (MEMs) force sensor to measure the magnetic force applied to individual beads and finite element modeling (FEM) of the EM applied field and gradient (7.5A, field = XXmTSJK

Steve: can you put in this value?--GET
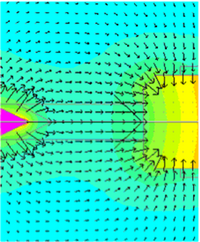
, gradient = 0.07 T/cm), the saturation magnetization of the beads was found to be 494,000 A/m and susceptibility was found to be 2.5. FEM of the magnetic field and gradient produced by the EM is shown in figure 3d. Force variation across the field of view is large (1.6 pN), but in principle it is known with micron-level precision and can be accounted for.
Results
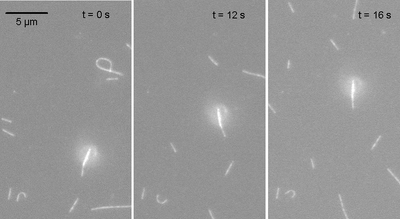
An inverted motility assay using conventional Drosophila melanogaster kinesin and the functionalized MTs was first carried out in a standard flow cell consisting of a microscope slide, double-sided tape and a #1 glass cover slip to verify attachment of the magnetic beads to MTs. Epi-fluorescence was visualized using a 100x N.A. 1.4 oil immersion objective (as opposed to the EM setup described above). Our best bead attachment preparations yielded 30-50% of the MTs having a single bead selectively attached to the minus end. Figure 2 shows time-elapsed images of a magnetic bead bound to the leading end of a polar MT moving at a rate comparable to that seen with control assays (~0.5 µm/s). However, the preparations were highly variable. Many MTs had no beads attached, were crosslinked to multiple beads (or multiple MTs were bound to one bead), or occasionally the bead was attached somewhere other than the minus end. In addition, non-specific binding of beads to the surface caused immobilization of some MTs. Previous experiments using smaller 1µm diameter beads (Dynal MyOne streptavidin) instead of 2.8 µm beads were more successful with selective attachment, however the larger beads were preferred for their much larger magnetic saturation moment.
Once bead attachment and motility was verified in a standard flow cell, the IMA was repeated in a Vitrotube™ and placed between the poles of the EM, having been previously positioned relative to the objective. Because the EM setup precluded visualization of the MT’s, success of bead attachment in the experimental assays shown is not known. Images of single moving beads in each IMA performed were taken while the EM current was cycled on and off.
The distance between the pole piece and the field of view was used to determine [math]\displaystyle{ grad Bvector }[/math] , the external magnetic field gradient. With the magnetic field gradient and dipole moment of the beads known, the force being applied to the beads is then defined as:
F vector = magnitude(mvector)(grad BVector)
assuming there is no external current at the location of the dipole and the beads are free to rotate and align with the external field. Thus the force on the bead is proportional to the magnitude of the dipole moment of the bead, and the gradient of the magnetic field [9]. With the 9% uncertainty of the bead moment, and 516 nm per pixel for image resolution, which correlates to our resolution of [math]\displaystyle{ grad Bvector }[/math] in the field of view, our force measurements are accurate to +/- 0.02 pN.
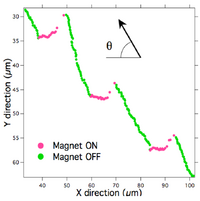
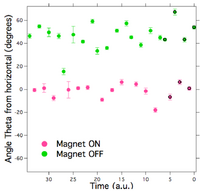
Images of single moving beads in each IMA performed were taken while the EM current was cycled on and off several times. (Computer controlled electromagnet and data acquisition, to be published elsewhere, LabVIEW software available on request.) Figure 3 shows a bead/MT traveling at a 50° angle away from the direction of the 0.7 pN cycled force. Each time the EM current was turned on, the bead/MT changed direction to align parallel with the force. Instead of maintaining that direction during each “off” cycle as expected, however, the bead/MT resumed its course ~50° away from the magnetic field. This redirection was seen a total of 15 times, 1 time per ON/OFF cycle.
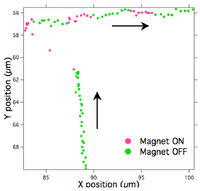
Figure 4 shows a bead/MT traveling perpendicular to a 2pN force. The first “on” cycle resulted in the bead/MT aligning parallel with the force, but moving in the opposite direction. If the bead were correctly positioned on the leading end of a single MT, it would be expected to move in the same direction as the applied force upon alignment. Nonetheless, as the bead/MT traveled against the force, the velocity decreased by an average of 45% with each “on” cycle and returned to normal velocity of about 0.8 µm/s upon each “off” cycle.
Discussion
Our constructed EM is capable of applying forces in the range of 0.1 to 10pN to Dynal 2.8µm beads. In comparison, the Holohan-Marston work demonstrated the ability to apply from 0-60pN of force on Dynal 2.8µm beads, with 6pN sufficient to pull bead-tailed actin filament off of a myosin motor coated surface and 0.6pN per µm length of actin to stall the filament [3]. However, in modeling performed by Gibbons et al., the stall force of a single kinesin motor was predicted to be 5pN [10]. They explain that cancellation of forces exerted by many motors results in a longitudinal force much smaller than the maximum force exerted by one motor. Also that the velocity of an MT in an IMA is the mean velocity of all attached motors, and whether the MT comes in contact with a low density (100’s) or high density (1000’s) of motors, most of the work is done by the small percentage of kinesin that stay attached longer. Our own force measurement required to slow down an MT in the IMA was 2pN and based on the Gibbons paper we speculate the density of active motors was low.
Our measured force required to steer an MT was 0.7pN and can be compared to a measurement by Hutchins et al. to steer the CoFe2O4 nanoparticle-coated MTs in the IMA [3b]. They estimate there are 1000 20nm particles packed on a 5µm long, 25nm diameter segment of the MT leading end and are able to use a permanent magnet to change the direction of such MTs in the IMA. Based on the known mechanical properties of MTs, Hutchins et al. estimates the amount of force required to bend one of their MT filaments is 10pN. By similar analysis, the flexural rigidity of MTs has been measured to be 3x10-23 Nm2 [11]. Bending an MT with a magnetic bead attached to the leading end can be modeled as a cantilevered beam. The spring constant of a cantilevered MT of length 10µm is ~10-7 N/m and a force of only 0.1pN is needed to deflect it through 1µm [12]. Our measurement of 0.7pN is in close proximity to this estimate and more than an order of magnitude smaller than that made by the Hutchins paper.
There are difficulties in interpretation of our experimental results shown here. Key questions are: 1) Why does the MT that is re-directed in figure 3 go back to the pre-directed direction when the magnet is off?; 2) Why does the MT in figure 4 travel in the direction opposite to the applied force? These unresolved questions may be explained by beads positioned on the middle or lagging end of the MT instead of on the minus end or by multiple MTs binding to one bead. However, it is difficult to be conclusive about what is really happening since only the beads (not MTs) can be visualized in the current EM testbed. Future work will require improving microscopy capabilities to visualize beads and MTs while applying magnetic forces. Optimization of the bead attachment process is also necessary to increase the level of control achieved with the EM. Possibilities in this direction include partially blocking the streptavidin sites on the beads prior to attachment in order to discourage crosslinking of the beads via MTs. Also, it is conceivable to isolate only the MTs attached to beads before use in the IMA, increasing the number of MTs with beads at the leading end in each assay.
Despite these difficulties, the experiments establish the plausibility of using an external electromagnetic field to direct the transport of kinesin-powered microtubule shuttles. Specifically here we have used a calibrated magnetic field gradient and bead magnetic dipole moment yielding known applied forces. The data in figure 3 clearly demonstrate an electromagnetic force repeatedly guiding the direction of a microtubule. Furthermore, figure 4 reveals the added potential to study biophysical properties of the kinesin-MT transport system. For example, by modifying the method to reliably place the magnetic bead on the lagging end of the MT to steer the MT in the opposite direction of the applied force, we will be able to characterize the force-velocity relationships for the system as a function of kinesin surface density and MT length. These experiments also demonstrate that the forces attainable from microfabricated magnetics are sufficient to manipulate the kineisn- MT transport system. The field gradient produced by our EM was 0.07 T/cm within our field of view. Comparatively, this much less than the 1 T/cm produced by microcoils fabricated for transport of beads with m = 7.2 x 10-14 A•m2 [13]. Also, since the magnetic moment of the 2.8µm diameter beads is an order of magnitude larger than this, microfabricated devices should be more than sufficient to produce forces for transport and sorting in the IMA.
Conclusions
We have demonstrated the ability to apply calibrated electromagnetic forces to beads specifically attached to microtubules. When in the IMA, the electromagnetic forces are sufficient to noticeably affect the speed and direction of motility of the MTs. Specifically, we have observed: that a 2pN force applied in the direction opposite to a MT slows its speed by approximately 45% and a lateral 0.7pN force was enough to repeatedly deflect the direction of motion by 50 degrees. The highlights of our method are that we are able to apply known forces to the IMA that are not destructive and in a manner that allows for performing multiple measurements at the same time. Additionally, the EM is thermally isolated from the flow cell to prevent heating of sensitive biological samples. We have bracketed the forces necessary to direct shuttles under the power of molecular motors and have demonstrated the feasibility of using integrated micromagnets in a flow cell for sorting and transport.
Acknowledgements
The authors wish to thank Dr. James E. Martin for support constructing and calibrating the EM and Erik D. Spoerke for polar MTs support. Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy’s National Nuclear Security Administration under Contract DE-AC04-94AL85000.
References
[1] H. Hess, G. Bachand, and V. Vogel. ‘Powering nanodevices with molecular motors.’ Chemistry - A European Journal. 2004, 10, pp 2110-6.
[2a] D. Erikson, D. Sinton, and D. Li. ‘Joule heating and heat transfer in poly(dimethylsiloxane) microfluidic systems.’ Lab Chip. 2003, 3, pp 141-9.
[2b] D. Ross, M. Gaitan, and L. Locasio. ‘Temperature Measurement in Microfluidic Systems Using a Temperature-Dependent Fluorescent Dye.’ Anal. Chem. 2001, 73, pp 4117-4123.
[3a] S. Holohan and S. Marston. ‘Force-velocity relationship of single actin filament interacting with immobilized myosin measured by electromagnetic technique.’ IEE Proc.-Nanobiotechnol., 2005, 152, pp. 113-119;
[3b] B. Hutchins, M. Platt, W. Hancock, and M. Williams. ‘Motility of CoFe2O4 nanoparticle-labeled microtubules in magnetic fields.’ Micro & Nano Letters, 2006, 1, pp. 47-52; B. Hutchins, M. Platt, W. Hancock, and M. Williams. ‘Directing transport of CoFe2O4 –functionalized microtubules with magnetic fields.’ Small, 2007, 3, pp 126-131.
[3c] J. Clemmens, H. Hess, R. Doot, C. Matske, G. Bachand, and V. Vogel. ‘Motor-protein "roundabouts": microtubules moving on kinesin-coated tracks through engineered networks.’ Lab on a Chip. 2004, 4, pp 83-6.
[4] J. Howard, A. Hunt, and S. Baek. Methods Cell Biol. 1993, 39, pp 137.
[5] S.J. Koch, G.E. Thayer, A.D. Corwin, and M.P. de Boer, ‘Micromachined piconewton force sensor for biophysics investigations.’ Applied Physics Letters. 2006, 89, pp.173901-1-4.
[6] A. Desai and T. Mitchison. ‘Microtubule polymerization dynamics.’ Annurev. Cellbio. 1997, 13, pp 83-117.
[7] W. Hancock and J. Howard. Modified from methods reported on the Kinesin Homepage: www.proweb.orb/kinesin.
[8a] K. Phelps and R. Walker. ‘NEM tubulin inhibits microtubule minus end assembly by a reversible capping mechanism.’ Biochemistry. 2000, 39, pp 3877-85.
[8b] E.D. Spoerke, to be published.
[8c] A. Hyman, et. al. ‘Preparation of modified tubulins.’ Methods in Enzymology. 1991, 196, pp 478-85.
[9] D. Griffiths. 1989. Introduction to Electrodynamics, 2nd ed. Prentice Hall, Englewood Cliffs, New Jersey.
[10a] F. Gibbons, J-F. Chauwin, M. Desposito, J. Jose`. ‘A Dynamical Model of Kinesin-Microtubule Motility Assays.’ Biophysical Journal. 2001, 80, pp 2515-26.
[10b] K. Visscher, M. Schnitzer, S. Block. ‘Single kinesin molecules studied with a molecular force clamp.’ Nature. 1999, 400, pp 184-9.
[10c] S. Block, C. Asbury, J. Shaevitz, M. Lang. ‘Probing the kinesin reaction cycle with a 2D optical force clamp.’ Proc Natl Acad Sci U S A. 2003, 100, pp 2351-6.
[11] B. Mickey and J. Howard. ‘Rigidity of microtubules is increased by stabilizing agents’. Journal of Cell Biology. 1995, 130, pp 909-917.
[12] J. Howard. 2001. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates, Sunderland Massachusetts.
[13]. Q. Ramadan, C. Yu, V. Samper, and D.P. Poener. ‘Microcoils for transport of magnetic beads.’ Applied Physics Letters. 2006, 88, pp 032501-1-3.
Comments by Outsiders
- Ramalldf 20:25, 25 April 2009 (EDT):Haha, I'm taking Zev Bryant's molecular motors class right now and for my project I'm writing a proposal that is based on developing a method that exploits molecular motors for DNA stretching purposes. He referred me to the paper by Vogel et al, so I googled "Vogel + piconewton force sensor" and this page was the first hit :D