Imperial College/Courses/2010/Synthetic Biology/Computer Modelling Practicals/Practical 2
Practical 2
Objectives:
- This practical will introduce you to the standard models for
- Constitutive Gene Expression.
- Activated and Repressed Gene Expression.
These models , along side the law of mass-action, are the models that are most commonly used in the computational side of synthetic biology. They will prove very useful for the rest of your course -especially the mini-iGEM - and you are expected to master them at the end this module.
Part I: Constitutive Gene Expression
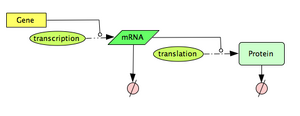
In this section, we explore a computational model to describe a constitutively expressed gene. The model is based on a simple interpretation of the central dogma: Gene -(transcription)-> mRNA -(translation)-> Protein, with both the mRNA molecules and the protein molecules being naturally degraded. If you need a quick refresh on the Central Dogma, have a look at the 'additional resources' section below.
The modelling parameters, used throughout this practical, are characteristic of the E.Coli bacteria.
| Model | CellDesigner Instructions |
|---|---|
|
|
Define the topology of the reaction network:
|
|
Following the law of mass action, we can write: |
|
Questions
The following questions constitue Part C of your coursework
- Question 1: Derive the steady-state expression of the [mRNA] concentration and the [Protein] concentration . Remember that steady-state means that both d[mRNA]/dt=0 and d[protein]/dt=0.
Now let us define the simulation constants...
- Question 2: In a bacterium that grows exponentially, the dilution rate corresponds to the (exponential)growth rate of the volume of a bacterium. It can be safely assumed that a bacterium divides once its volume has doubled. Knowing that the typical cell division time for e-coli is 30-40min (use 35 minutes), what is the dilution rate?
- Question 3: Knowing that average number of mRNA molecules per gene is 2.5 in E.Coli, what is the average transcription rate ? Keep in mind that the problem only gives the mRNA half life, not the actual degradation rate (see the exponential decay model for more info)
- Question 4: Knowing that the average number of proteins per gene is 1000 in E.Coli, what is the average translation rate ?
You are now ready to run the simulations with CellDesigner. Define all the necessary kinetics laws for the model, and create all the appropriate parameters.
- Question 5: Run a simulation, and comment on the simulation outputs (mRNA and Protein). Pay special attention to the transient phase and the steady-state.
- Question 6: From a Synthetic Biology point of view, this motif can be seen as a 'Protein Generator'. One might be interested in controlling the steady-state protein output level of this device. Using the 'parameter scan' function, run a simple sensitivity analysis on each of the 4 parameters, within a 10% range of their default value. Illustrate, and describe briefly, how each parameter impacts the protein steady state.
Part II: A Simplified Model for Constitutive Gene Expression
Before moving to other types of genes, it is interesting to explore the quasi-steady-state assumption on the mRNA molecules expression.
- From the previous simulations, you might have noticed that the concentration of mRNA reaches steady-state very quickly, compared to the protein concentration.
- This suggests that we could consider that the [mRNA] concentration is always at steady state , i.e. [math]\displaystyle{ \frac{d[mRNA]}{dt}=0 }[/math] all the time. This model means that we want to apply a quasi-steady-state assumption on the [mRNA] molecules.
| Model | CellDesigner Instructions |
|---|---|
|
|
|
|
Following the law of mass action, we can write: |
|
Questions
The following questions should also feature in Part C of your coursework
- Question 7: Taking into account the quasi-steady-state assumption on the [mRNA], work-out the value of 's', and 'd' with regards to [math]\displaystyle{ k_1, k_2, d_1, d_2 }[/math], so that the two models are equivalent.
- Question 8: Simulate the full model, alongside with the quasi-steady state approximation. When using the parameters from the previous section, comment on how good this approximation seems to be.
- Question 9: When and why do you think such a reduced model would be useful ?
Part III: Activated and Repressed Gene Expression
Very few genes are known to have a purely constitutive expression, most genes have their expression controlled by some outside signals (DNA-binding proteins, Temperature, metabolites, RNA molecules ...). In this section, we will particularly focus on the study of DNA-binding proteins, called transcription factors. These proteins, when binding to a promoter region, can either have an activation effect on the gene (positive control), or a repression effect (negative control). In prokaryotes, control of transcriptional initiation is considered to be the major point of regulation. In this part of the tutorial, we investigate one of the most common model used to describe this type of interactions.
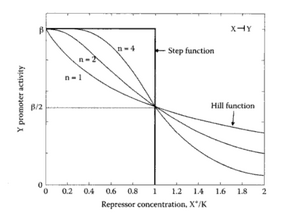
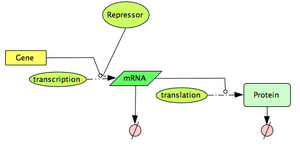
Let's first consider the case of a transcription factor acting as a repressor. A repressor will bind to the DNA so that it prevents the initiation of transcription. Typically, we expect the transcription rate to decrease as the concentration of repressor increases. A very useful family of functions to describe this effect is the Hill function:
[math]\displaystyle{ f(R)=\frac{\beta.{K_m}^n}{{K_m}^n+R^n} }[/math].
- The Hill function can be derived from considering the transcription factor binding/unbinding to the promoter region to be at equilibrium (similar to the enzyme-substrate assumption in the Michaelis-Menten formula).
- This function has 3 parameters: [math]\displaystyle{ \beta, n, K_m }[/math]:
- [math]\displaystyle{ \beta }[/math] is the maximal expression rate when there is no repressor, i.e. [math]\displaystyle{ f(R=0)=\beta }[/math].
- [math]\displaystyle{ K_m }[/math] is the repression coefficient (units of concentration), it is equal to the concentration of repressor needed to repressed by 50% the overall expression, i.e [math]\displaystyle{ f(K_m)=\frac{\beta}{2} }[/math]
- [math]\displaystyle{ n }[/math] is the Hill Coefficient.
| Model | CellDesigner Instructions |
|---|---|
|
|
Define the topology of the reaction network:
|
|
Hill function for transcriptional repression:
|
|
|
We can therefore write: |
|
Questions
The following questions are part of section D of your coursework:
- Question 1: Analysis of the Hill function
the parameter n of the Hill function determines the profile of the Hill function. Plot the Hill function for well chosen values of n (we recommend n=1, n=2 and n=3). All the other parameters of the function can be set to 1. Describe the evolution of the Hill function. Why can we regard it as a switch function?
- Question 2: Analysis of the Repression
We assume that the concentration of repressor remains constant. Plot [math]\displaystyle{ [Protein]= f(time) }[/math] for a few well-chosen repressor concentrations between 0 and 1000. Describe your results
- Question 3: The Transfer Function
We still assume that the concentration of repressor remains constant. We want to establish the transfer function between the [repressor] concentration and the protein steady-state level. To do so plot [math]\displaystyle{ [Protein]_{steady-state} = F([Repressor]) }[/math] where the repressor concentration varies from [0 to 1000].
- Question 4: Unfortunately in practice, repressor genes are leaky, that is the transcription is not simply regulated by the repressor concentration but also has a constant term. A repressor gene with a leakiness coefficient [math]\displaystyle{ \alpha }[/math] has a transcription rate [math]\displaystyle{ k_1(\alpha+(1-\alpha)\frac{{K_m}^n}{{K_m}^n+R^n}) }[/math].
- Repeat the simulations of Question 2: for a leakiness coefficient of 10% and comment
- Repeat the simulations of Question 3: for a leakiness coefficient of 10% and comment
- Question 5: Suggest an application where this genetic circuit might be useful. Discuss (in qualitative terms) what characteristics the repressor should have for your chosen application.
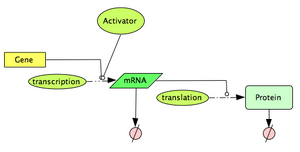
Part IV: Activated and Repressed Gene Expression
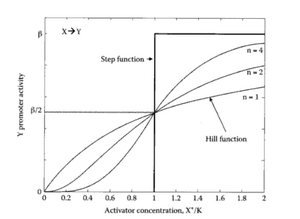
Now, let's consider the case of a transcription factor acting as an activator. An activator will bind to the DNA so that it promotes the initiation of transcription. Typically, we expect the transcription rate to increase as the concentration of activator increases. Once again, the Hill type function will be useful to describe the interaction effect. It is slightly different from the previous one: [math]\displaystyle{ f(R)=\frac{\beta.{A}^n}{{K_m}^n+A^n} }[/math].
| Model | CellDesigner Instructions |
|---|---|
|
|
Define the topology of the reaction network:
|
|
Hill function for transcriptional activation:
|
|
|
Following the law of mass action, we can write: |
Questions
The following questions are also part of section D of your coursework:
- Question 6: Analysis of the Activation
We assume that the concentration of activator remains constant. Plot [math]\displaystyle{ [Protein]= f(time) }[/math] for a few well-chosen activator concentrations between 0 and 1000. Describe your results
- Question 7:The new transfer function
We still assume that the concentration of activator remains constant. We want to establish the transfer function between the [Activator] concentration and the protein steady-state level. To do so plot [math]\displaystyle{ [Protein]_{steady-state} = F([Activator]) }[/math] where the Activator concentration varies from [0 to 1000].
- Question 8: Again in practice, the genes are leaky. An activator-gene with a leakiness coefficient [math]\displaystyle{ \alpha }[/math] has a transcription rate [math]\displaystyle{ k_1(\alpha+(1-\alpha)\frac{{A}^n}{{K_m}^n+A^n}) }[/math].
- Repeat the simulations of Question 6: for a leakiness coefficient of 10% and comment
- Repeat the simulations of Question 7: for a leakiness coefficient of 10% and comment
- Question 9: Suggest an application where this genetic circuit might be useful.
Part V: Additional Resources