Imperial College/Courses/2010/Synthetic Biology/Computer Modelling Practicals/Design
Complementary Session: Introduction to the Design of Biological circuits
Goals of the session
- This session aims at introducing to you the basic tools and techniques of design (without which no computer-assisted design is possible.
- The material presented in this session will not count towards your coursework.
- However, it should prove useful for the rest of your course, especially the mini-iGEM.
- Takeaway message:
- designing simple pathways is possible, albeit hard
- in practice it gets very complicated, very fast...
Foreword
Design of a synthetic biological pathway (whether it is computer-assisted or not) is in general a very complicated affair. Typically, a list of specifications (and tolerances) has been drawn for the synthetic pathway. Based on pre-existing designs (found in nature or not) and their inspiration, a biological designer will then propose a pathway (topology+genes) that may meet this specifications. Computer simulations are very valuable tools to check and if need be modify the design of a synthetic pathway. They are not however, without their problems and it is crucial that synthetic biologists are aware of the practical limitations of computer modelling.
The first set of limitations concern the verification phase. you must, by now, be aware of the complexity of biological pathways and how fast unpredictable behaviours may emerge. In the case of the repressilator, 3 genes are enough to generate a pathway with 'interesting' properties.
More generally:
- the behaviour depends on the (potentially many) parameters of the system
- we may not know them with enough accuracy - sometimes not at all
- a small change in a parameter may lead to a totally different behaviour (bifurcation)
- initial conditions are also liable to have an influence (the arguments regarding the parameters mostly apply to the initial conditions too)
Browsing the space of admissible parameters to check whether a proposed design meet some initial specifications therefore becomes - very quickly- a very difficult computational problem.
The second set of limitations is far worse unfortunately . Even if there is a subspace of parameters for which the synthetic pathway seems to meet your initial specifications, your model and simulations may mislead you. It may indeed be too simple or not have any predictive power. Possible reasons include:
- some basic properties of the cell have a significant impact on the effective dynamics of pathways. Take for instance the growth rate:
- it appears in the dilution term of proteins (easy to incorporate into the model)
- but is also affects in a highly nonlinear way the gene copy number
- it affects the concentration of free and bound RNAp and therefore the level of transcription etc..
- some modules in your system may be very hard to model (if at all possible)
- for instance transport of molecules through a membrane and diffusion phenomena can be modelled but it becomes complicated fast
- in a model, errors pile up so much so that after a while the predictive power of your model is negligible.
- your synthetic pathway may 'cross-talk' with natural pathways; since we are not able to model the whole metabolism of the cell this crosstalk effect can not be assessed.
Now, all is not lost! Designing simple pathways with predictable properties/functions is indeed possible, even without the extensive use of software.
Preliminary Simplifications
A great deal of the design work takes place on a sheet of paper. It is therefore important to develop an intuition of the functioning of the various elements and how they combine. To make our task simpler, it is customary to make a few (usually easily justifiable) assumptions. The following assumptions are the most common ones:
Initial Conditions
- for a constititutive gene, both protein and mRNA are at steady state
- for an inducible gene, the same assumption holds but the steady state depends on the concentration of inducer
- write the general expression of the steady state of protein and mRNA for a activated gene
- write the general expression of the steady state of protein and mRNA for a repressed gene
Time scales
- Binding reactions occur very fast, so fast we can reliably assume they are instant
- mRNA reaches its steady state after a few minutes
- Proteins reach their steady states in hours
Simplified Gene Expression Model
Finally it is customary to approximate the gene expression profile by the simplified model of practical 2, where it is assumed that mRNA is at steady state. It is also custom to overlook the evolution of mRNA unless it is stricly needed as for instance with riboswitches... In practice it is assumed that the production rate of proteins is constant.
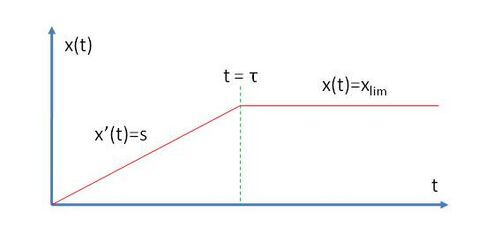
In the case of a constitutive promoter or an inducible promoter for which the inducer does not enter any other biochemical pathway (this includes degradation) the gene expression profile simplifies into a simple ramp profile.
- Let us deal with the case of a constitutive promoter first; How do the parameters of the ramp model refer to parameters of the standard constitutive gene expression model?
- Same question for an activated gene
- Same question for a repressed gene
Although very simple, the ramp model is very powerful and has been widely used in software such as rovergene that check whether a proposed-network topology may meet certain requirements (for instance oscillations, steady state of protein 1 between two specified values etc...).
| The Ramp Approximation |
|---|
Ideal Induction
As you must know by now, the relation between trancription rate and inductor concentration is modelled with a sigmoidal Hill function.
to simplify things it is assumed it is ideal that is of infinite sharpness. Induction therefore depends only on the switch value Km.
A Basic Timer
Timers are in theory very easy to design (in practice they are fiendishly hard to build, you will see why). They also are ideal toy-systems to learn the basics of design in biological engineering.
The simplest design rests on the following 3 ideas
- 1) Switching on a gene is achieved when the concentration of the gene activator crosses the activation threshold
- 2) With an inducible gene, the rate of protein production depends on the concentration of inductor
- 3) consequently the time it takes for that protein to go over a defined threshold will depend on the concentration of inductor (if the gene is strong enough)
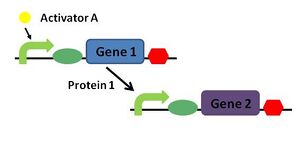
The simplest timer design therefore consists of two activated genes in cascade. We note A the activator of gene 1. Gene 1 synthesizes protein 1 (P_1) which activates Gene 2, which itself produces protein (P_2).
| Model | The simplest timer |
|---|---|
|
The synthetic pathway can be modelled as:
|
- Preliminary analysis
- sketch the expected behaviour of the system (for both protein 1 and 2).
- Prove that the first gene has to be strong enough for the second gene to be switched on
- With the ramp model, estimate how long it will take before the production of the second protein is switched on
- Now let's run simulations for the following parameters and comment the results
- Activation parameters
- For promoter 1, K_1=100
- for promoter 2, K_1 = 500
- all the hill functions are infinitely sharp
- initial concentration of inducer A_0=250;
- both genes are non-leaky
- Protein 1: production rate s_1=100 ; degradation rate = 0.1
- Protein 2: production rate s_2=50 ; degradation rate = 0.5
- Activation parameters
- Unfortunately genes are leaky and hill exponents are not infinite...
- Redo the simulations for p=1 and q=2;
- Swap the hill exponents and do the simulations - comment your results
- the first gene is now leaky witha leakiness coefficient of 10% -p=1 and q=2 - comment your results
Autoregulation of a Protein Concentration / A Negative Feedback Loop
Analogies with design of electronic circuit are plentiful. Let us consider another example, which happens to be found very often in nature too (in e-coli for example see Uri Alon book). Pathways are often designed so that the concentration of a given protein be at a given value and may not deviate much from this given value.
- The simplest way to ensure that the concentration of a protein be set to a given value is to have it produced under a constitutive gene.
- We wish a protein P , whose degradation rate is d, to be kept constant to a concentration C_0. What should the production rate of the gene synthetsizeing P be?
- Now, let us imagine that the concentration of P is perturbed so that it drops from C_0 to C_1; Prove that the constituve gene will bring it back to C_0; estimate how fast this will happen. Comment on these results
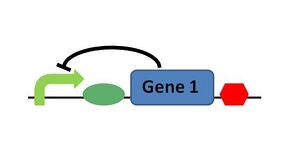
A classic trick used in electronics to control a voltage and keep it to a given value is to use a negative feedback loop. Such a trick is easily transposed into the realm of synthetic biology: all it takes is a protein that represses itself.
| Model | Active Control through Self-repression |
|---|---|
|
The ODE system can be written as:
|
- Preliminary analysis
- We want the steady state of the protein to be C_0; what relation binds a,d,K_m and n?
- Show that the maximal production rate (a) is larger than it would be with a constitutive promoter.
- sketch the expected behaviour of the system - show that the system will overshoot the target concentration.
- Now let's run simulations for the following parameters
- Activation parameters: n=2; K_m=100
- The gene is non-leaky
- Protein 1: degradation rate = 0.1 ; Target concentration =1000
- First use an intial protein concentration of 0
- Analyse how the system reacts to perturbation by varying the initial concentration ( say from 0 to 2000)
- Compare the performance of the autorepressed system to the performance of a constitutive gene
A bump generator
Finally, we want to design a system that produces a protein for a limited amount of time - and we wish to control the time the system produces.
- A constitutive gene is always on, so it is not a suitable solution.
- Solutions involving a single gene do exist. for instance let us consider the following strategy
- Switch on a gene (activator concentration above activation threshold)
- Then wait for concentration of activator to drop below the activation threshold, which effectively switches off the gene
- What mechanisms can make the activator concentration drop below the activation level?
- Explain why this will be slow and cumbersome
Fortunately a simple solution with two genes exists.Its principle is simple:
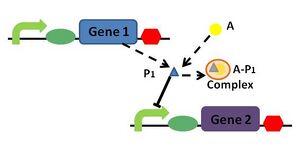
- The synthesis of a protein P_1 is ruled by a strong constitutive promoter
- Protein P_1 represses Gene 2; therefore Gene 2 is effectively switched off
- Repression of Gene 2 is lifted by the introduction of a molecule A that binds to P1
- Gene 1 then produces more protein 1 to restore it to its steady state and silence gene 2
| Model | The bump generator |
|---|---|
|
P_1 Constitutively expressed by Gene 1 P_1 Represses Gene 2 A may bind to P_1 as follows: |
- Preliminary analysis
- sketch the expected behaviour of the system (for both protein 1 and 2, and molecule A).
- Prove that the first gene has to be strong for the second gene to be switched off
- Now let's run simulations - Describe your results and comment on them
- Protein 1: production rate s_1=100 ; degradation rate d_1= 0.1
- Protein 2: maximum production rate s_2=50 ; degradation rate d_2= 0.5
- Activation parameters: K_m=300; hill exponent n=2
- Binding constants: k_1=100; k_2=105000;
- initial concentration for A: A_0=5000;
- Make the initial concentration of A vary and comment on the length of the bump and the amount of protein 2 that is produced