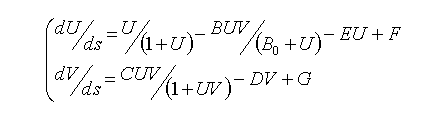IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/Conclusion/Future Works

Possible Extensions of the 2D Model

Introduction

Should we extend the 2D model?

• In the 2D model we have assumed so far that

- the leakage terms were negligible

- the growth of both prey and predator is not commended by a term depending on an exponent alpha

• Both qualitative assumptions can be justified from a biological point of view. But from the point of view of our analysis how robust are our results with regards to these assumptions?
• Before discussing the influence of variability on our study, it is worth stressing that in the discussion that follows we strictly remain within the realm of Dynamical Systems.
• Thus we overlook all possible stochastic elements in our system such as the distribution of a certain parameters over the population of cells. Equivalently we assume the distribution is Dirac.

Variability in biology

• Variability in biology is in general large, consequently parameter estimations are often 'ballpark estimates'.
• The data analysis part of our project is a good example variability in Biology. For instance from the normalised fluorescence plot of GFP vs AHL we can get a decent estimate of the parameter C0. The assumption alpha=1 also seems to hold for the experimental data - although an acceptable fit could be also be obtained for a range of values of alpha around 1.
• As a rule of thumb, an error of 10% is usually considered acceptable for such biological data,as it is thought to have little influence on the main characteristics of a biological system.

The consequences of variability in biology

• With Dynamical Systems we cannot afford such luxury unfortunately.
• As the analysis of the 2D model shows two types of behaviors can be obtained for our system: stability and oacillations. Each behaviour is associated with a subspace of parameters. Consequently the tolerance on the parameters (and on all similar assumptions) cannot be measured in percentages but with regards to the location of the parameters in the space of parameters and in particular to how far to the border between stability and oscillations they are.

Conclusion

• It follows from this little discussion that in order to fully validate our existing analysis of the 2D model we need to

- extend the model to include leakage terms and an exponent alpha

- study its behaviour at the vicinity of null leakage terms and alpha=1

- either prove that our existing analysis does not correspond to a pathological case

- if this fails discuss the possibility of oscillations for small values of leakage and alpha almost 1

• In the following sections you can find a few qualitative results we have gathered on the extended model. We - again - broke down the complexity of the analysis by studying

- the influence of the leakage terms first

- then the influence of the exponent

- finally the whole model

Leakage Terms

Introduction

• Biological Interpretation of the Leakage Terms

• Model with Leakage Terms

The dimensionless form of the model with leakage terms is

2D Model with Leakage:

General Results

• The Dissipative Terms (due to washout in chemostat) ensure that trajectories remain bounded
• We can therefore apply Poincare-Bendixson again
• If we ensure all steady point are unstable then we will have oscillations
• Simulations show that we can obtain some oscillations

Influence of Leakage terms

• The Leakage Term F 'pushes' the vector field to the left (Warning: it is not mere translation) and consequently:

- the Steady Point (0,0) disappears

- any Limit Cycle will be pushed to the left also hence may get very close to Y-axis

• The Leakage Term G 'pushes' the vector field upward (Warning: again it is not mere translation), which confers to the system a string of Practical Advantages:

- We cannot have steady points on the X-axis

- Hence any limit cycle will not get too close to X-axis

- Suggestion: If we can measure the predators instead of the preys, let's do it!!

Exponent

Introduction

• We assume the leakage terms are negligible (or zero). But this time we introduce an exponent in the model. The dimensionless form of the model is:

2D Model with Exponent: File:Model-exponent.png

• Interpretation

alpha>1 => cooperation

General Remarks

• The Dissipative Terms (due to washout in chemostat) also ensure that trajectories remain bounded
• We can therefore apply Poincare-Bendixson again
• If we ensure all steady point are unstable then we will have oscillations

Alpha=1 is a Limit Case

• For alpha larger than 1

- Some steady points are stable

- Origin (0,0) becomes stable point (all the time)

- On X-axis we have two other steady points (one of which is also stable)

• Therefore we have a Big Problem:

- We are unlikely to get oscillations

- Trajectories likely to converge to one of the Steady stable Points

- Yet we cannot rule out existence of a Limit Cycle

- Poincare - Bendixson just says trajectories will converge to stable point or limit cycle

- We would have to study basin of attraction of Limit Cycle

- We would have dependency on initial conditions (Again!!!)

• We did a few a simulations for alpha more than 1 and were unable to get some oscillations

• For alpha smaller than 1

- We do not have these problems with points on X-axis

- Origin (0,0) always saddle point (Jacobian non defined actually)

- On X-axis we have another steady points that can be made unstable

• - With alpha less than 1 , We end up in a situation similar to the model we have studied and expect oscillations

Extended 2D Model

Final Model We now consider both leakage terms and an exponent in the growth terms of the model. The dimensionless form of the model now becomes:

Generalised 2D Model File:Model-2Dgeneralised.png

Expected Behaviour: A mixture previous results

• We can hope to get oscillations with alpha larger than 1

- Leakage term F help stabilise the system as it expels (0,0)

- Leakage term G can be used to stabilise the system as pushes steady points off the X-axis

• Advantage of the result (if confirmed) :

Our study done 'at the border' alpha = 1 will be more representative / trustworthy

We can extend the data-analysis part of the project and seek a better fit by introducing a new parameter in the interpolation model

• If we cannot get oscillations for alpha larger than 1 our system may be really hard to build!!!

NB:These qualitative results have not been proved. We are confident of their validity. Proving them - and simulating the most interesting cases is a job we leave for next year.