IGEM:IMPERIAL/2006/Before the Jamboree/MIT Site

Project Website
Imperial College iGEM 2006 Website on OpenWetWare
- Full Documentation
- 100's of Photographs
- Extensive Modelling
- Lab Notebook
- And much more!
Project Summary
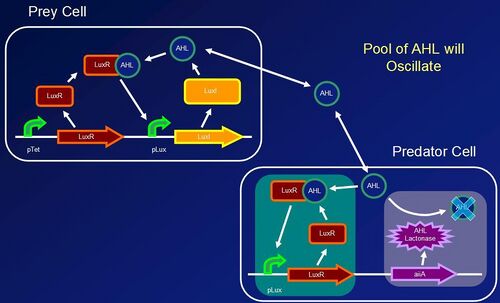
The major goal of Imperial College’s 2006 entry into the iGEM competition was to create a stable biological oscillator, improving on past designs such as Elowitz’s repressilator. The team investigated into natural biological oscillators and sought to mimic Lotka-Volterra predator-prey interactions with a molecular system. The model was adapted to molecular interactions between prey (n-acyl homoserine lactone (AHL)) and predator (AiiA (AHL-lactonase) + LuxR). The design strategy of the project was an engineering based cycle of specification, design, modeling, testing, and implementation. Parts were constructed and individually tested before the final construct was assembled. Our ongoing parts testing shows correlation to our mathematical models, suggesting that the design could be successful.
Introduction
Predator-prey interactions form stable oscillations with frequencies which can be calculated precisely given certain assumptions. The team decided to model the biological oscillator on the basis of predator-prey interactions hoping that this novel approach would lead to success. Since one of the key assumptions to the model is the self dependent growth of prey, a positive feedback loop for the production of AHL was implemented in E. coli strain DH5a. Furthermore, a separate cell was constructed to sense the AHL molecules in the surrounding environment and respond by producing AiiA. This will result in the AHL being degraded, or in terms of the model, being “eaten by the predator”. Since AiiA production is dependent upon the concentration of AHL molecules, the action of AiiA itself, leading to a decrease in AHL concentration, would result in less AiiA being produced at a later time. The advantage of a two cell construct instead of previous one cell construct designs is that Paremeters can be changed easily by altering cell ratios. AHL is a suitable molecule to mimic the prey behavior. since it can be detected by a transcriptional regulator (LuxR) and therefore promote it's own growth. Also it easily diffuses outside of the cell as well having a complementary predator molecule AiiA. The team attempted to use as many parts from the Registry of Standard Biological Parts, which are outlined in the biological parts section. Once a stable oscillator has been created, several future applications into biological computing and synchronization become accessible.
Biological Parts
Below are all the parts designed for the predator-prey oscillation system. Parts actually sent to registry can be found here.
Final Constructs
- <bbpart>J37015</bbpart> – Final Prey Cell
- F2620 (AHL Receiver)
- C0261 (LuxI)
- I13504 (GFP Reporter)
- <bbpart>J37036</bbpart> – Final Predator Cell – Polycistronic Design
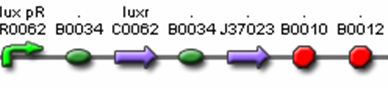
- R0062 (Lux pR, AHL induced promoter)
- B0034 (RBS)
- C0062 (LuxR)
- B0034 (RBS)
- J37023 (AiiA w/ LVA & FLAG)
- B0015 (terminator)
- <bbpart>J37035</bbpart> – Final Predator Cell – Monocistronic Design
- R0062 (Lux pR, AHL induced promoter)
- B0034 (RBS)
- C0062 (LuxR)
- I13033 (terminator + Lux pR)
- B0034 (RBS)
- J37023 (AiiA w/ LVA & FLAG)
- B0015 (terminator)
Test Constructs
- <bbpart>J37016</bbpart> (Polycistronic Predator Cell Test Construct)
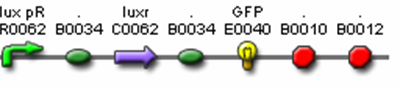
- R0062 (Lux pR, AHL induced promoter)
- B0034 (RBS)
- C0062 (LuxR)
- I13504 (GFP Reporter)
- <bbpart>J37020</bbpart> (Monocistronic Predator Cell Test Construct)
- R0062 (Lux pR, AHL induced promoter)
- B0034 (RBS)
- C0062 (LuxR)
- I13033 (terminator + Lux pR)
- I13504 (GFP Reporter)
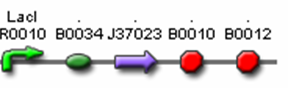
- <bbpart>J37022</bbpart> (AiiA Test Construct)
- J04500 (LacI promoter + RBS)
- J37023 (AiiA w/ LVA & FLAG tag)
- B0015 (terminator)
New Individual Protein Coding Sequences
- <bbpart>J37023</bbpart> (AiiA Protein Coding Sequence with LVA & FLAG immunotag)
Experiments & Results
Testing constructs above were made to characterise the parts necessary to build the biological oscillator using standard ligation procedures. The FLAG immunotag was added to the existing registry AiiA part with an LVA tag (<bbpart>C0060</bbpart>) using Polymerase Chain Reaction (PCR) methods. The resulting protein coding sequence was then ligated to the other BioBrick parts.
BioBricks composing the test constructs and the final oscillator were engineered and a number of important results were extracted from the modelling and testing stages: i) The test constructs/BioBricks representing the different parts of the oscillator were characterised from testing in E.Coli (DH5α) (testing page). ii) The model of the test constructs, which included experimental data, predicted stable oscillations as output of the full system (modelling pages). iii) The influence of specific system parameters on the frequency, amplitude and stability of the oscillations was investigated with the Lotka-Volterra model (LV model).
Modelling
Assumptions for Modelling
- General assumptions on gene expression modelling:
- Quasi-steady state hypothesis on mRNA expression.
- Gene activation can be approximated by Hill equations.
- Assumptions linked to the quorum sensing:
- As a first approximation, we assume that luxR and AHL molecules form a heterodimer (even if it has been found that the complex formed is more complicated)
- The concentration of the heterodimer is in equilibrium with the concentration of AHL
- LuxR is constitutively produced and reaches steady state before AHL production begins. [LuxR] in the prey can be considered constant
- The degradation rate of luxR and AHL-lactonase is due to the growth dilution which, in this case, is controlled by the chemostat
- AHL is diffusing freely throughout the system
Differential Equations Derived
The following three differential equations completely describe the concentrations of AiiA, LuxR and AHL in our oscillator.
[math]\displaystyle{ \frac{d[AHL]}{dt}= \frac{a[AHL]}{(a_0 + [AHL])} - \frac{b[AiiA][AHL]}{(b_0 + [AHL])} - \delta_{deg}[AHL] }[/math]
[math]\displaystyle{ \frac{d[luxR]}{dt} = \frac{c[AHL][luxR]}{(c_0 + [AHL][luxR])} - \delta_{deg}[luxR] }[/math]
[math]\displaystyle{ \frac{d[AiiA]}{dt} = \frac{c[AHL][luxR]}{(c_0 + [AHL][luxR])} - \delta_{deg}[AiiA] }[/math]
Applications
Once we are able to create a biological oscillator, we can then move to synchronise several biological computer paving the way for an internet-like system controlled by bacteria. Further developments to electrical interfacing could mean that communication between electrical and biological devices would be seamless. This can potentially integrate the existing infrastructure and novel biological approaches so the current technology would not be drastically displayed, but gradually replaced by better biological machines. Moreover, the quest for self-reproducing machines has finally succeeded. Wouldn’t it be great if our computers upgraded themselves? Made themselves faster every 30 minutes? Genetically engineered bacteria have this potential and are only limited by their lifespan and the biological reaction rates. Unfortunately, biological reaction rates are relatively slow, so when compared to electrical signals, consider 100 years ago when we knew very little about electricity and how to harness the power of electricity. Biological engineering is at that stage now, and we cannot expect to surpass in a few years the engineering foundations that have been perfected throughout the ages.
Future Extensions
Once a stable biological oscillator has been achieved, the next step is to connect two oscillators together and investigate into how two populations synchronize themselves. This could lead to more information on the mechanism behind cellular communication and steps necessary to control it, especially in terms to controlling the amplitude and frequency of biological oscillations. One major drawback to working with biological systems is their inherent noise and ability to mutate. It is yet to be seen if any of these factors could affect the robustness of a biological oscillator. Furthermore, electrical to biological interfaces are the next step in bringing the power of biological systems to fruition. This could lead to an internet communication using existing infrastructure between bacterial colonies, and the possibilities are limitless, just as they are with the internet today.
The Team
- Undergraduates
- Christin Sander (Bioengineering)
- Deepti Aswani (Biology)
- Farah Vohra (Bioengineering)
- Jiongjun Bai (Electrical Engineering)
- John Sy (Bioengineering)
- John Chattaway (Biology)
- Jonathan Wells (Biology)
- Tom Hinson (Biochemistry)
- Advisors
- Prof. Richard Kitney
- Prof. Paul Freemont
- Dr. David Mann
- Dr. Kirsten Jensen
- Vincent Rouilly
- Chueh-Loo Poh
- Matthieu Bultelle
- Contributors
- Prof. Tony Cass
- Dr. Anna Radomska
- Dr. David Leak
- Dr. Mauricio Barahona
- Dr. Danny O'Hare
- Ms. Susan E. Wryter
- Mr. David Featherbe
- Dr. Geoff Baldwin
- Ciaran Mckeown
- Dr. James Mansfield - Chemostat
- Special thanks for their support to
- The European Comission
- Imperial College Deputy Rector's Fund
- Imperial College Faculty of Engineering
- Imperial College Faculty of Life Sciences
<html> <script type="text/javascript" language="javascript"> var sc_project=1999432; var sc_invisible=1; var sc_partition=18; var sc_security="3a523ad5"; </script>
<script type="text/javascript" language="javascript" src="http://www.statcounter.com/counter/frames.js"></script><noscript><a href="http://www.statcounter.com/" target="_blank"><img src="http://c19.statcounter.com/counter.php?sc_project=1999432&java=0&security=3a523ad5&invisible=1" alt="hit counter script" border="0"></a> </noscript> </html>