Final Report
Modeling Background Radiation with the Poisson Distribution
Experimentalists: Kirstin G. G. Harriger and Brian P Josey
Junior Lab, Department of Physics & Astronomy, University of New Mexico
Albuquerque, NM 87131
kharrig1@unm.eduAbstract
Poisson statistics govern many important processes in physics, such as background radiation and radioactive decay. In this experiment, we explore the Poisson distribution as a model for background radiation. Background radiation events in the lab were counted using a scintillator connected to a photomultiplier tube and a computer. The data was gathered over 9 trials with time periods ranging from 0.01 seconds to 1 second. We compared the standard deviation of the data to what the theoretical standard deviation would be if that data was represented by a Poisson distribution. We also predicted the average number of background radiation events in the lab for a one second time period with data from the first 8 trials. Data was then gathered for a one second time period in the 9th trial to compare to the predictions. In the one second time period there were an average of 33 ± 6 radiation events, and the average of the predictions was 31 ± 6 events. Our data was demonstrated to be representative of a Poisson distribution, both qualitatively and quantitatively.
Introduction
SJK 02:35, 18 December 2010 (EST)

Good introduction.
The Poisson distribution is a discrete probability distribution and it is characterized by a function that gives the probability of a discrete random number being equal to some value1. Specifically, it expresses the probability of a number of discrete events occurring within a time frame if the timing of each event is independent of the timing of the previous event, the events are rare, i.e. unlikely to be simultaneous, and there is a definite average rate of events2. If the known average rate is [math]\displaystyle{ \lambda }[/math] then the probability that there are exactly k occurrences is equal to3
- [math]\displaystyle{ f(k; \lambda) = \frac{\lambda^k e^{-\lambda}}{k!} }[/math]
Statistical questions can be answered with only the average rate being known for a given Poisson process4. One statistical quantity that is relevant to our experiment is the theoretical standard deviation, the square root of the average, of the Poisson Distribution5. Consequently, the average and the standard deviation are not independent of each other6. If it can be shown that the standard deviation is significantly close to the theoretical standard deviation of the Poisson distribution, then the data is modeled a Poisson distribution quantitatively. The formula that shows this relationship is7
- [math]\displaystyle{ \sigma = \sqrt{\overline{\lambda^2} - \overline{\lambda}^2} = \sqrt{\lambda} }[/math]
Another characteristic of the Poisson distribution is that the average rate of events measured for one time period can be used to predict the average rate of another time period by using a factor that converts between the time periods8. If the average rate was measured over 0.01 seconds and you wanted to predict the average rate for 1 second, then you would multiply the measured average rate by 100. The data is likely to represent a Poisson distribution if the predicted average rate for a given time period is significantly close to the average rate measured for that time period.
The Poisson distribution has many applications in physics, especially in modeling radioactive decay processes9 and cosmic background radiation. This is because these processes are governed by particle characteristics which can be treated discretely10 and counted, the timing of each of event is independent of the timing of the last, and the events are rare and unlikely to be simultaneous. Additionally, it is not difficult to get a known average of events from one time period to find a theoretical standard deviation and predict an average number of events for another time period.
We measured the number of background radiation events in a standard physics teaching laboratory at 5000 ft elevation. After we gathered the data, we analyzed it using the two characteristics of the Poisson distribution described above: the theoretical standard deviation, and the prediction of an average rate from one time period to another time period. We compared trends in our data as the average rate increased for increasing time periods to the known trends in the Poisson distribution under the same circumstances, and we demonstrated the trends graphically to show further evidence that our data represented a Poisson distribution.
Materials & Methods


A scintillator connected to a photomultiplier tube, Tracor Norther Model TN-1222, see Figure 1, was used to detect ionizing background radiation. When the scintillator detected radiation, it would create a small flash of light in the ultraviolet range which was detected by the photomultiplier tube. The photomultiplier tube would then convert the light into a single voltage via the photoelectric effect 11. This signal was detected by the computer, a J and J Workstation with Intel Celeron CPUs of 2.26GHz and 2.27GHz and 1.96 GB of RAM, with it's internal MCS card. We used a Spectech Universal Computer Spectrometer set to 1200V, see Figure 2, in order to amplify the signal generated by the photomultiplier tube.
The Spectrum Techniques UCS 30 software counted each signal voltage picked up by the card in the computer as an event. The data output by this software contained the size of the dwell time, and the number of radiation events that occurred in each instance, or window, of the given dwell time. This data was then saved into files that were manipulated with MATLAB v. 2009a. In this experiment we used the dwell times: 10, 20, 40, 80, 100, 200, 400, 800 ms to gather data in order to determine the prediction for one second. We then used a dwell time of 1 second to gather data to compare to the prediction. Each run of the software collected data for 2047 windows for the given dwell time.
The fractional probability in Table 2 was calculated by dividing the number of windows in which a given number of events occurred by the total number of windows. The predicted average radiation events per second in Table 3 was calculated by dividing 1 second by a dwell time in seconds and then multiplying that by the average number of events per window for that dwell time.
The MATLAB code used to make Figure 3 is as follows:
- plot(A4,B4,A5,B5,A6,B6,A7,B7)
- xlabel('Number of Events')
- ylabel('Fractional Probability')
- title('Fractional Probability of a Given Number of Radiation Events')
- legend('Trial 4: 0.08s Dwell Time', 'Trial 5: 0.1s Dwell Time', 'Trial 6: 0.2s Dwell Time', 'Trial 7: 0.4s Dwell Time')
The variables A4-A5 contain all the numbers of events that were detected for Trials 4-7, and the variables B4-B7 contain the fractional probabilities that the numbers of events will occur for Trials 4-7.
The MATLAB code used to make Figure 4 is as follows:
- plot(x,y)
- xlabel('Square Root of the Average Number of Events per Window')
- ylabel('Calculated Standard Deviation')
- title('Relationship Between Theoretical and Calculated Standard Deviation')
The variable x contains the standard deviations calculated as the square root of the average number of events per window, and the variable y contains the standard deviation calculated with the standard deviation function in MATLAB.
Results
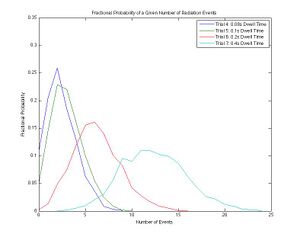
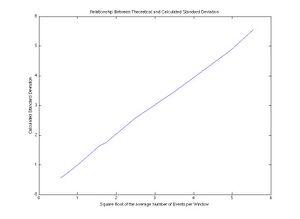
Table 1: The sheets in this table show the raw data generated by the USC 30 software for each of the 9 trials. The first 13 rows show information about the run. The rows after row 15 show the data gathered by the computer from the scintillator and PMT. The first column after row 15 shows the channel numbers, of which there is one for each window in the run; the second column shows the cumulative dwell time for the trial; and the third column shows the number of radiation events detected for the given channel.
Table 2: In the first column the possible number of radiation events per window are listed from lowest to highest for each dwell time. The second column shows how many windows in which a given number of radiation events were detected for that dwell time. For instance if there were 100 windows in which 3 radiation events were detected, 3 would be in the first column and 100 would be in the second column next to it. The third column shows the fractional probability that there will be a given number of events in a window.
Table 3: The first row shows the average number of radiation events per window as calculated directly from the data for each dwell time. The second row shows the standard deviation of the data as the square root of the average for each dwell time, and the third row shows the standard deviation as directly calculated from the data for each dwell time. The fourth row shows the percent error between the two standard deviations. The fifth row shows the predicted average rate per second from the data for the dwell time.
Discussion
There are several trends characteristic of a Poisson distribution and can be demonstrated graphically and our data shows these trends, see Figure 3. As the window size increases, the average number of events and the standard deviation also increase. The peaks of the curves, showing the most probable number of events for a given dwell time, move from being the y-intercepts to the right in the direction of increasing numbers of events. The curves become more symmetric and begin to look like Gaussian distributions. The curves flatten out as the highest probability becomes less distinct from the other probabilities. This is the result of the relationship between the average number of events and the standard deviation in a Poisson distribution. The curves spread out along the x-axis as more possible numbers of events are detected for longer windows. Since the curves clearly demonstrate the trends associated with a Poisson distribution developing as the average number of events increase, the graph indicates qualitatively that the data represents a Poisson distribution.
There is a close relationship between the two standard deviations, the one calculated in the normal way and the one that is characteristic of data in a Poisson distribution, the square root of the average. These two values are supposed to be equal for data that represents a Poisson Distribution, see Figure 4. The difference between the two deviations never exceeds 5.15%. The graph of the two deviations is very nearly linear, demonstrating that the two deviations are approximately equal. This indicates quantitatively that the data represents a Poisson distribution.
An important characteristic of the Poisson distribution is that the average rate of events measured for one time period can be used to predict the average rate of another time period. The data from Trials 1-8 was used to predict the average number of radiation events during one second as can be seen in Table 3. The average of these predictions was 31 ± 6 events per second and the measured rate was 33 ± 6 events per second. The percent difference between these two values is 6.06%, which suggests the predictions were relatively good ones.
Conclusion
In this experiment, background radiation events were counted over time periods varying from 0.01 seconds to 1 second during 9 trials. The events were detected using a combined scintillator and photomultiplier tube whose output signal was amplified with a spectrometer before being fed into a computer. The data gathered was shown to follow a Poisson distribution based on graphical trends and statistical characteristics. Predictions were made for the average rate of radiation events in a one second time period based on data from the first 8 trials. In the one second time period there were an average of 33 ± 6 radiation events, and the average prediction was 31 ± 6 events. We found that our data represented a Poisson distribution, and based on this we could make accurate predictions about the average number of events over time for background radiation.
Acknowledgments
I would like to thank the professor for this course, Dr. Steve Koch, the TA, Katie Richardson, the original creator of the experiment, Dr. Michael Gold, and especially my fellow experimenter, Brian P. Josey.
References
- Wikipedia Article on the Probability Mass Function
- Measurements and their Uncertainties by I. Hughes & T. Hase, Copyright 2010, Published by Oxford University Press Inc., pg. 30
- Wikipedia Article on the Poisson Distribution
- Journal of the American Statistical Association, Vol. 49, No. 266 (Jun., 1954), pg. 255
- Prof. Gold's Lab Manual, pg. 60
- Measurements and their Uncertainties by I. Hughes & T. Hase, Copyright 2010, Published by Oxford University Press Inc., pg. 29
- An Introduction to Error Analysis by John R. Taylor, Copyright 1982, Published by University Science Books, pg. 249
- An Introduction to Error Analysis by John R. Taylor, Copyright 1982, Published by University Science Books, pg. 247
- Measurement and Detection of Radiation by Nicholas Tsoulfanidis, Copyright 1995, Published by Taylor and Francis, pg. 37
- Radiation Mechanics: Principles and Practice by Esam M. A. Hussein, Copyright 2007, Published by Elsevier Ldt., pg. 8
- Wikipedia Article on the Scintillators