DNAmazingProcess
<html><head> <style type="text/css"> .main { margin: 0 auto; width: 804px;border-style:solid; border-width:5px; }
- logo{ margin:10px 0 0 52px; display:block; background:url('http://openwetware.org/images/7/74/Banner20.png') 0 0 no-repeat; width:700px; height:200px; text-indent:-9999px;}
.navbox { position: relative; float: left; }
- menu{ background:url('http://openwetware.org/images/3/3f/Menu_bg.png') 0 0 no-repeat; width:643px; height:100px; margin:51px 0 0 78px; padding-top:100px}
- menu li{ float:left;}
- menu a{ font-size:30px; color:#000000; line-height:1.2em; text-decoration:none; letter-spacing:-1px;}
.nav1{ padding:26px 0 0 37px;} .nav2{ padding:16px 0 0 30px;} .nav3{ padding:36px 0 0 17px;} .nav4{ padding:16px 0 0 19px;} .nav5{ padding:26px 0 0 30px;}
- menu .nav1 a:hover{ color:#bb0e0e}
- menu .nav2 a:hover{ color:#ca6509}
- menu .nav3 a:hover{ color:#3f9711}
- menu .nav4 a:hover{ color:#0ca0ce}
- menu .nav5 a:hover{ color:#8606c5}
</style> </head>
<header> <a href="index.html" id="logo">DNAmazing asfsaf. Smart. Effective</a> <nav>
</nav> </header>
</html>
Background Information
DNA Origami
DNA Origami has emerged as one of the most promising tools for DNA self-assembly nanostructures. The techniques has been coined by Rothemund in 2006 (1) and extensively exploited. Thank to the efforts of scientists in the field, DNA origami now can enable the building of custom-shaped DNA nanostructures with a high degree of accuracy and complexity. DNA Origami structures have been used to study single-molecular chemical reactions, to assemble water-soluble probe tiles for label-free RNA hybridization (2).
DNA Origami future applications and developments
Potential applications of DNA Origami in the future are the modeling complex protein assemblies, the building of molecular electronics or plasmonic circuits created on the DNA Origami boards, or even molecular factories with nanomachines operated on complex networks constructed by DNA Origami technique (1). Some of these applications may require the connection between DNA structures and other novel materials or devices such as carbon nanotubes, nanowires, gold nanoparticles, DNA nanomachines, etc. Sticky ends have been suggested as the best solution so far (3). Sticky ends are double helix DNAs with one longer single strand containing unpaired base pairs. The unpaired base pairs of sticky ends can act as a link between DNA Origami and other DNA or biological devices through the hydrogen bonds of complementary base pairs. In addition, the ends of sticky strands can be functionalized with chemical groups (4).
Another requirement for future applications of DNA Origami is the design complexity. The application of DNA Origami for the molds of large scale nanoelectronic circuits and platforms for DNA machines definitely demand a software to reduce the tedious process of building the scaffold, determining the crossover positions.
Traditional CAD programs for DNA Origami
Process
The Overview of DNAmazing Program
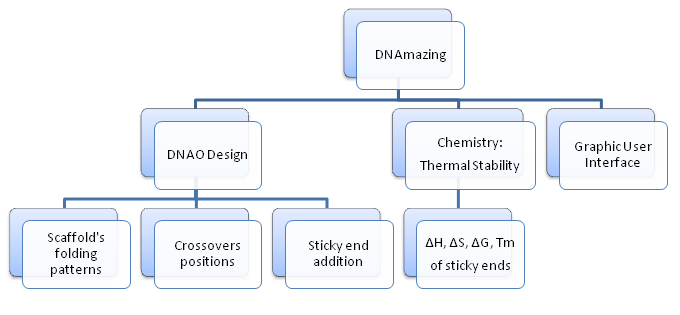
DNAmazing program consists of three main modules: Design, Chemistry, and Graphic User Interface (GUI).
The programming language is C# and the integrated development environment (IDE)is Microsoft Visual Studio 2010.
The Design is the backbone of the program which provides basic functions of a DNA Origami design tool: receiving information about the DNA Origami structures (shapes, sticky ends) and returning the necessary information of staple and scaffold sequences to synthesize the structures in labs.
The Chemistry: implementing Nearest-Neighbor method, thermal stability of DNA sticky end is estimated by calculating [math]\displaystyle{ \Delta H^o }[/math], [math]\displaystyle{ \Delta S^o }[/math], [math]\displaystyle{ \Delta G^o }[/math], and melting temperature [math]\displaystyle{ T_m }[/math]. In addition, these thermodynamic values assist in the sticky end generation process by ensuring that proposed sticky end is not stably bound to the scaffold strand.
The GUI allows users work on the Design and Chemistry in a user-friendly, interactive interface.
The Design
Basic Dogmas of Design
The Design of 2D DNA Origami in DNAmazing follows the principles which were laid out in Rothermund's first paper in 2006 (1). The basic idea of DNA Origami is to fold a DNA helix into a desired shape. The DNA helix in DNA origami is made from 2 different single strands: a single, long, and continuous strand making up the pattern of the origami is called the scaffold strand; the second strand made from the continuous connection of several short, single DNA fragments, or staple strands. The staple strands are bound to the scaffold via the complementary base-pair interaction, constructing the structure of DNA origami. In addition, the staple stands form crossovers to keep the scaffold strand in the desired shape.
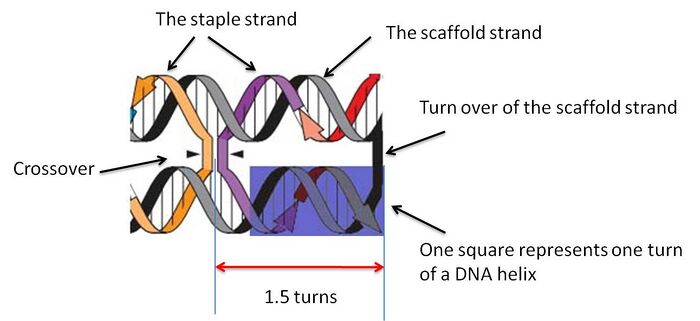
For designing purpose, the desired DNA origami is conceptually divided into several small helical segments, in which one segment is equivalent to one turn of the folded helix. Each segment is represented as one square shown in the program, and is numbered for designing convenience. The labeling is done from left to right, and from bottom row to the top. The non-integer number of bases pair per turn: 10.67 (5) will be approximated as 11 base pairs. The DNA helix is folded by forming several crossovers in the staple strands; these crossover indicates the position where a staple strand switches to binding to another segment of the scaffold strand. These crossover positions only occur at locations where DNA twist places at its tangent point between helices which is apart by any odd number of half-turns. In this project, we will stick to 1.5 turns (1).
Throughout the software, there are 2 coordinate systems which are used to refer a specific square in the DNA Origami structures. The labeling mentioned in this part is the matrix coordinate. The other is the scaffold coordinate which will be described later in 6.2.3 Generation of scaffolding pathways.
Inputting parameters
Recognizing the fact that the conventional input of existing programs may not be convenient for large and complex structures, DNAmazing adopts a very different way: a lithography-like way.Instead of drawing the scaffold way, which may be difficult and even impossible for complicated designs, users will input the dimensions of a rectangle that encloses their desired structure. The dimensional units are the number of helices/squares per row and per column. The users will achieve their final desired shape by eliminate the unwanted squares. The elimination id done by inputting the number of the unwanted squares (null squares).
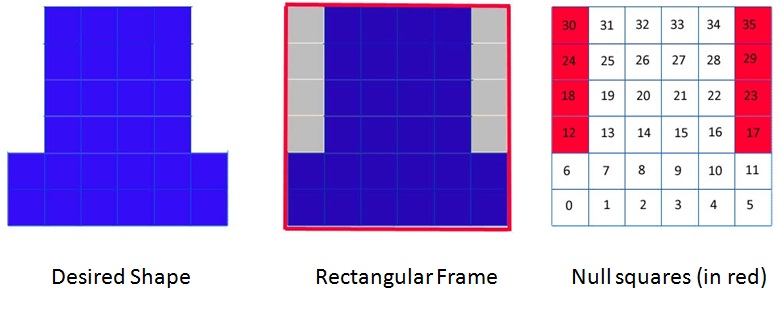
In the above example, the desired DNA Origami shape is enclosed by a rectangular frame 6 squares x 6 squares. There are totally 8 null squares: 12,18,,24,30,17,23,29,35.
Generation of scaffolding pathways
One of the unique features of DNAmazing is its ability to automatically generate the scaffolding pathways. For the existing programs, users have to manually design the folding of the scaffold into the desired shapes. This process is tedious for complex structures such as smiling faces in Rothermund's paper. In DNAmazing, users only have to conceptualize the DNA Origami structures into series of squares which was described in the previous part. This is definitely less time-consuming and much easier.
Basically, the process of generation of scaffold folding pathways is to thread the scaffold strand to all the squares, and each square is visited only once. This is very similar to the algorithm of the Hamiltonian circuit (or the Hamiltonian path). In the graph theory, a Hamiltonian circuit is a path in an undirected graph that visits each vertex exactly one (6). Another example of Hamiltonian circuit is the problem of a business man to visit all the cities only once to deliver goods.
Each square in DNA Origami is modeled as a vertex which can be linked to its 4 adjacent neighbors in 4 directions, but not diagonal neighbors. The null squares are isolated squares and there is not be any links to them, and "null" square is not included in the folding pathway. The scaffolding path starts with the first square and extend by adding one of 4 neighbors of the first square. A Hamiltonian circuit can be solved by exploring all the possible paths that satisfy the condition.The process is repeated until it can no longer extend because of there are not any possible choices or the path has passed through all squares. If the latter happens, the process is done and a scaffolding pathway is successfully generated. In the former cases, the program will take one step back and explore other choices.
By using the algorithm of the Hamiltonian circuit, DNAmazing is able to find all the possible scaffold pathways. However, not all of these ways are reasonable for the DNA Origami. A filter must be included to select the paths which are suitable for DNA Origami. Below are some rules which we use in the filtering process:
- The first square is either square 0 or the square at the middle of the first row
- If the first square is square 0, the scaffold should run continuously and only turn over to the next row at either of the two ends. If the first square is the middle one of the first row, the last square in the scaffold way must be on the right of the first square.
- The scaffold should not run in the vertical direction.
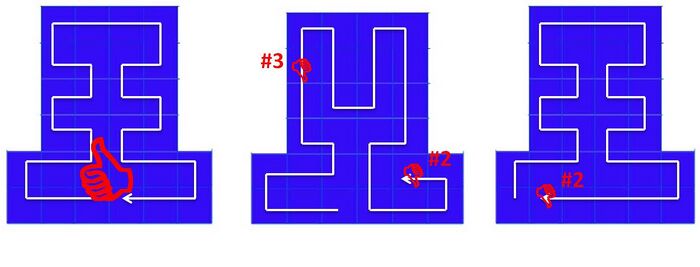
The result of this stage is a 1D matrix containing the ordinal numbers of the squares that the scaffold passes through. For instance,the scaffold way in the above figure will be presented as C=[2,1,0,6,7,8,14,13,19,20,26,25,31,32,33,34,28,27,21,22,16,15,9,10,11,5,4,3]
Determination of crossover positions
The next step in the Design part is the determination of crossover positions. Crossovers are the positions where the staple strands switch to bind to another segment of the scaffold located on the next row. The crossovers are crucial to the folding of the scaffold strand; in fact, they are the only linkages which prevent the helix from unfolding. The basic principle to determine the positions of crossovers was laid out by Rothermund: the spacing between crossovers in 2D DNA Origami structures must be an odd number of half turn. In other words, 2 vertically adjacent staples meet at their tangent points every an odd number of half turn. Thus, the staples will be in the least strained state at the crossovers. Particularly, in this project, we will stick to 1.5 turns as the unit for the spacing of crossovers.
The algorithm to determine the crossover positions starts with the generation of an ArrayList, which is a matrix with flexible dimensions. We named it PosCros. The Poscros Arraylist is used to add the squares which contain the crossover position. The first element of PosCros is always the first element in the scaffolding pathway. The next elements are determined based on the category of the previous element; the categorization is done based on the relative distance between the element and the closest turning point of the scaffold.
Generation of Sticky ends' Sequence
Sticky ends serving as an extra ends of a staples should not interfere with the scaffold folding, and must not bind to the scaffold, in the formation of DNA Origami. So, sticky end sequences must not have any stable binding to any segment of the scaffold. To generate sticky end sequences, DNA sequences of a defined length are generated randomly. The newly generated sequences are then to be examined for its binding ability via the binding free energy. Sequences which have a rather stable binding with any position in the scaffold are discarded. Only those without stable scaffold binding are kept and can be used as sticky ends’ sequences.
To determine whether the sticky end would have any stable binding to the scaffold, one needs to know binding energy of the sticky end to every sequence in the scaffold. In addition, a threshold below which the binding is considered stable is also required.
Calculation of binding energy
The Sticky end sequence given is mapped along the scaffold length and the binding energy [math]\displaystyle{ \Delta G^o }[/math] is calculated for each match/mismatch binding. The calculation was done using the formula and complete thermodynamic database for internal single mismatches discussed in SantaLucia’s studies (2006) (7). The formula and parameters are shown bellow:
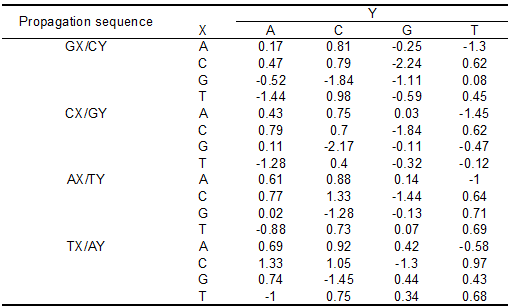
Nearest-neighbor [math]\displaystyle{ \Delta G^o }[/math] increments (kcal/mol) for internal single mismatches next to Watson-Crick pairs in 1 M NaCl
For example, consider the total binding energy of following DNA duplex. The mismatch base pair is bold:
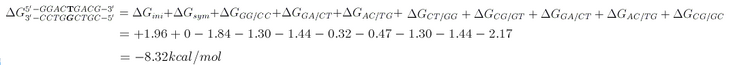
In our program, [math]\displaystyle{ \Delta G_{sym} }[/math] and [math]\displaystyle{ \Delta G_{ini} }[/math] were not included in the [math]\displaystyle{ \Delta G }[/math] calculation as sticky ends are merged with the staple sequences
Set up a threshold
To determine if the mismatched complement between the sticky ends and the scaffolds are stable or unstable, a threshold of binding energy ([math]\displaystyle{ \Delta G^o }[/math]) is required. Binding energy less than or equal to this threshold would be consider stable. There should not be an absolute threshold value for every DNA sequence with different length. Longer DNA sequences require lower [math]\displaystyle{ \Delta G^o }[/math] for a stable binding. Therefore, the threshold is set up as a variable calculated based on the sequence length: Let n be the length of DNA sequence. If n is even, the threshold is calculated as follow:
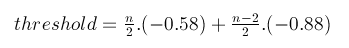
if n is odd, then the formula to calculate the threshold is:
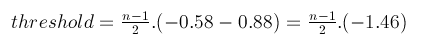
In the above equation, -0.58 is the binding energy between 5’-TA-3’/3’-AT-5’, and -0.88 is the binding energy between 5’-AT-3’/3’-TA-5’. This means that the right side of the equation equal the binding energy of the complement 5’-(AT)n-3’/3’-(TA)n-5’of the same length. In other words, there would be no binding between the sticky end and scaffold which is more stable than the least stable Watson-Crick fully complemented DNA duplex
Generation of staples sequence
This final step provides the most meaningful and necessary information for users, the staples sequence. Together with the scaffold sequence, the staple sequence is the most important parameter to generate DNA Origami structures in wet lab experiments. The program firstly obtains the sequence of the scaffold strand extracted from the genome of Mp13 virus. This can be done by calculating the number of squares in the DNA Origami=>number of base pairs=> get from the beginning until that point. The sequence of the complementary strand to scaffold strand will be determine after that. This complementary strand is divided into smaller fragments. Each fragment’s length is 11 base pairs. For the purpose of merging, each fragment is cut into 2 smaller fragments: one contain 6 base pairs and the other 5 base pairs. Thus we have 2 types of staples: A with 6 base pairs and B with 5 base pairs. Basically, A is always at the 3’ end while B is at 5’ end. The next step is to append the sticky ends into the staples. The location of appending can be either the beginning or the end of the square. A merging process of staples (which includes sticky ends) to form the crossover must be done
The prediction of the thermal stability of the duplex produced from sticky end
Predict the thermal stability of short DNA duplex which is formed upon the binding of the sticky end and its complementary single-stranded strand.
The capability to estimate the thermal stability will aid in numerous applications such as (i) predicting the stability of a local sequence on DNA duplex, or of a probe-gene complex, (ii) calculating the melting temperatures of short sequences in hybridization experiments, (iii) determining the optimal length of the probe oligomer to produce stable duplexes with the sticky ends (8,9).
Research has shown that the thermal stability of duplex is affected by sequence information and base compositions. However, the sequence of DNA strand is the major determinant of [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ H^o }[/math], [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ S^o }[/math], and [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ G^o }[/math]. We apply the nearest-neighbor (NN) method to determine the transition enthalpy, entropy, free energy, and melting point of short DNA duplex (7,8). This method calculates those thermodynamic values using the stacking interaction between Watson-Crick neighboring bases in the DNA strands.
DNAmazing program will not only assist in random generating stick ends attached to pre-determined positions on DNA Origami, but also allow users to input their preferred sequence information of the sticky ends. Since different sequences have different thermal stability (represented by [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ H^o }[/math], [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ S^o }[/math], and [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ G^o }[/math]) upon binding, knowing those thermodynamic values is crucial to study the function and applications of the sticky ends.
There are many groups have dedicated researching on NN method to determine [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ H^o }[/math], [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ S^o }[/math], [math]\displaystyle{ \Delta }[/math][math]\displaystyle{ G^o }[/math], and [math]\displaystyle{ T_m }[/math] of short DNA oligomers and have arrived on the same formula as demonstrated below. However, since difference researches used different starting materials (short DNA oligomers, polymers, etc.), the values for one parameter slightly vary. We have chosen the latest results obtained by SantaLucia et al (7) to incorporate into our software.
- [math]\displaystyle{ \Delta H^o_{} = \Delta H^o_{ini} + \Delta H^o_{sym} + \Delta H^o_{AT term.} + \Sigma \Delta H^o_{stacking}\! }[/math]
Where [math]\displaystyle{ \Delta H^o_{} }[/math] is the helix initiation enthalpy of the transition process; [math]\displaystyle{ \Delta H^o_{sym} }[/math] is the symmetry term only applies to self-complementary duplexes, accounting for the enthalpy difference between a duplex formed from a self-complementary sequence and a duplex formed from 2 complementary strands; [math]\displaystyle{ \Delta H^o_{AT term.} }[/math] is applied for each end of a duplex that has a terminal AT, accounting for the end-fraying caused by AT base pair; [math]\displaystyle{ \Sigma \Delta H^o_{stacking} }[/math] is the total of enthalpy of propagation step in the sequence.
For example:
- [math]\displaystyle{ \begin{align} \Delta H^o_{} (5'-CGTTGA-3') & = \Delta H^o_{ini} + \Delta H^o_{sym} + \Delta H^o_{AT term.} + \Sigma \Delta H^o_{stacking} \\ & = 0.2 + 0.0 + 2.2 + ( - 10.6 - 8.4 - 7.6 - 8.5 - 8.2) \\ & = -40.9 (kcal/mol) \\ \end{align} }[/math]
[math]\displaystyle{ \Delta S^o }[/math], [math]\displaystyle{ \Delta G^o }[/math] are calculated using the same formula (7) above.
There are 10 propagation steps, 1 initiation, and 1 terminal AT correction to make up a total of 12 NN parameters shown in Table 1. These values are obtained via multiple linear regression of the results from differential scanning calorimetry (DSC) of 108 short DNA sequences.
| Propagation step | [math]\displaystyle{ \Delta H^o }[/math] (kcal/mol) | [math]\displaystyle{ \Delta S^o }[/math] (e.u.) | [math]\displaystyle{ \Delta G^o }[/math] (kcal/mol) |
|---|---|---|---|
| AA/TT | -7.6 | -21.3 | -1.00 |
| AT/TA | -7.2 | -20.4 | -0.88 |
| TA/AT | -7.2 | -21.3 | -0.58 |
| CA/GT | -8.5 | -22.7 | -1.45 |
| GT/CA | -8.4 | -22.4 | -1.44 |
| CT/GA | -7.8 | -21.0 | -1.28 |
| GA/CT | -8.2 | -22.2 | -1.30 |
| CG/GC | -10.6 | -27.2 | -2.17 |
| GC/CG | -9.8 | -24.4 | -2.24 |
| GG/CC | -8.0 | -19.9 | -1.84 |
| Initiation | +0.2 | -5.7 | +1.96 |
| Terminal AT penalty | +2.2 | +6.9 | +0.05 |
| Symmetry correction | 0.0 | -1.4 | +0.43 |
The melting point of short DNA chain, defined as the temperature at which half of double-stranded DNA sequences have dissociated, is calculated as following:
- [math]\displaystyle{ T_m = \frac{\Delta H^o \times 1000} {\Delta S^o + R \times \ln( \frac{C_t}{x} ) - 273.15} }[/math]
where [math]\displaystyle{ C_t }[/math] is the total molar strand concentration. For nonself-complementary duplexes x=4, and for self-complementary, x=1.
NN method is just an approximation because it neglects the secondary interactions in the DNA duplexes (we assume that the DNA duplexes undergo two-state transition), and the heat capacity [math]\displaystyle{ C_p }[/math] is constant over different temperatures. To reduce such inaccuracy in calculation, short DNA oligomers (less than 30 base pairs) were used to minimize the secondary interaction within the DNA molecule.
Sodium dependence of [math]\displaystyle{ \Delta S^o }[/math] and [math]\displaystyle{ \Delta G^o }[/math]
The entropy and free energy calculated from formula (1) above apply at 37oC and 1M NaCl. To extend the results to various salt condition, the following correction formulae have been derived by (***)
- [math]\displaystyle{ \Delta S^o [Na^+] = \Delta S^o [1M NaCl] + 0.368 \times N/2 \times ln[Na^+] }[/math]
- [math]\displaystyle{ \Delta G^o [Na^+] = \Delta G^o [1M NaCl] + 0.114 \times N/2 \times ln[Na^+] }[/math]
where N is the total number of phosphate in the duplex and [Na^+] is the total concentration of monovalent cations ([math]\displaystyle{ Na^+ }[/math], [math]\displaystyle{ K^+ }[/math], [math]\displaystyle{ NH^{4+} }[/math]) in the solution. [math]\displaystyle{ \Delta H^o }[/math] is assumed to be sodium-independent.
To calculate the value of [math]\displaystyle{ \Delta G^o }[/math] at temperature different than [math]\displaystyle{ 37^o }[/math], the following equation is used:
[math]\displaystyle{ \Delta G^o = \Delta H^o - T\Delta S^o }[/math]
in which T is in Kelvin, [math]\displaystyle{ \Delta H^o }[/math] is in cal/mol, and [math]\displaystyle{ \Delta S^o }[/math] is in entropy units (e.u.). [math]\displaystyle{ \Delta H^o }[/math] and [math]\displaystyle{ \Delta S^o }[/math] are assumed to be independent of temperature.
References
1. Rothemund, P. W. K. (2006). "Folding DNA to create nanoscale shapes and patterns". Nature. 2006 Mar 16;440(7082):297-302.
2. Ke, Y., Lindsay, S., Chang, Y., Liu, Y., Yan, H. (2008). "Self-assembled water-soluble nucleic acid probe tiles for label-free RNA hybridization assays". Science. 2008 Jan 11;319(5860):180-3.
3. Li, Z., Liu, M., Wang, L., Nangreave, J., Yan, H., Liu, Y. (2010). "Molecular behavior of DNA origami in higher-order self-assembly". J Am Chem Soc. 2010 Sep 29;132(38):13545-52.
4. Pearson, A. C., Pound, E., Woolley, A. T., Linford, M. R., Harb, J. N., Davis, R. C. (2011). "Chemical alignment of DNA origami to block copolymer patterned arrays of 5 nm gold nanoparticles". Nano Lett. 2011 May 11;11(5):1981-7.
5. Ke, Y., Douglas, S. M., Liu, M., Sharma, J., Cheng, A., Leung, A., Liu, Y., Shih, W. M., Yan, H. (2009). "Multilayer DNA origami packed on a square lattice". J Am Chem Soc. 2009 Nov 4;131(43):15903-8.
6. Baumgardner, J., Acker, K., Adefuye, O., Crowley, S. T., Deloache, W., Dickson, J. O., Heard, L., Martens, A. T., Morton, N., Ritter, M., Shoecraft, A., Treece, J., Unzicker, M., Valencia, A., Waters, M., Campbell, A. M., Heyer, L. J., Poet, J. L., Eckdahl, T. T. (2009). Solving a Hamiltonian Path Problem with a bacterial computer. J Biol Eng. 2009 Jul 24;3:11.
7. SantaLucia, J. and D. Hicks (2004). "The Thermodynamics Of Dna Structural Motifs". Annual Review of Biophysics and Biomolecular Structure 33(1): 415-440.
8. SantaLucia, J., H. T.m Allawi, et al. (1996). "Improved Nearest-Neighbor Parameters for Predicting DNA Duplex Stability†." Biochemistry 35(11): 3555-3562.
9. Breslauer, K. J., R., Frank, et al. (1986). "Predicting DNA duplex stability from the base sequence." Proceedings of the National Academy of Sciences 83(11): 3746-3750.