Capillary Number (Ca) - Christopher Sparages
Introduction
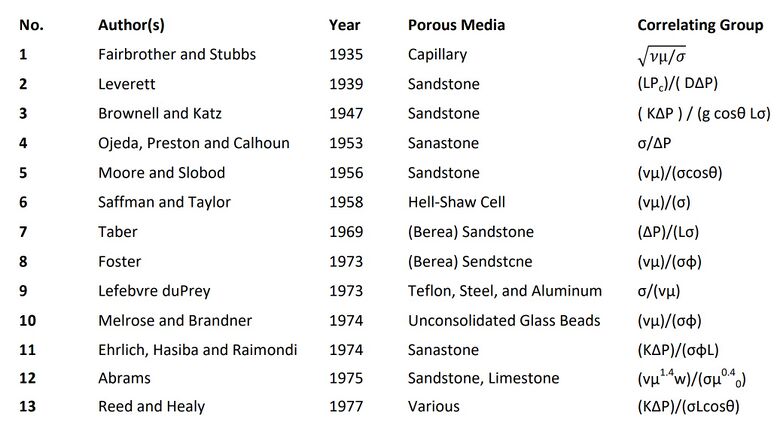
The capillary number (Ca) is a dimensionless number and it represents the relation between viscous forces and capillary forces, which occur between two immiscible liquids. Over the years, the capillary number has been represented by a series of different forms across literature with one of the most common one being the formalism by Saffman and Taylor (Figure 1, No. 6).[1]
The Saffman-Taylor definition for capillary number describes the ratio of (vμ)/σ with v as the fluid velocity, μ as the fluid viscosity, and σ as surface tension between the two immiscible liquids or gas and liquid. The capillary number is used to determine which forces dominate in a specific scenario.[2] When Ca>>1, surface forces are dominated by the viscous forces. When Ca<<1, surface forces dominate the viscous forces. making the viscous forces negligible.[1]
Capillary Number Theory

The capillary number theory was originally developed by basing the idea off of capillary tube bundles and Darcy's law.[4] Darcy's law predicts that residual oil will not be able to be moved until it reaches a critical capillary number. The goal of the experiments driving this theoretical discovery was to determine the saturation movement of this residual oil after it is in contact with water forcing imbibition, which is the expansion of solid when it absorbs water.[5] Putting this theory to the test through experiments has made it possible for progress to be made in developing enhanced methods to contribute towards gas recovery operations. The capillary number is used for example in chemical flooding situations where a decrease in capillary number corresponds to a decrease in remaining oil saturation.[4]
Applications
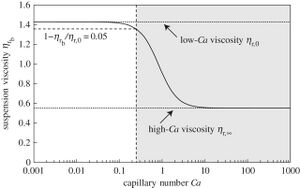
Bubble Suspension
As mentioned above the capillary number is a representation of forces between two immiscible liquids (gas or liquid). In the case of bubble suspension, the interaction is between a liquid and gas. A large reason for studies conducted with bubble suspension is to learn more about to develop models, characterize, and control the flow of the respective gas.[7] In order to achieve these goals, rheology tests are conducted while values for viscosity, velocity, and surface tension are taken see how capillary number effects the behavior of this bubbling. Comparing the bubble viscosity to the capillary number, results can be seen that with an increase in capillary number there is a sigmoidal response in the bubble viscosity (Figure 3).[6]
Chemical Flooding
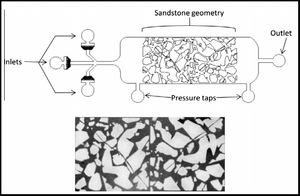
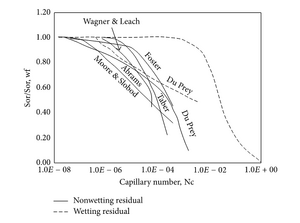
The capillary number theory is also used as a basic theory for chemical flooding. Chemical flooding includes things such as oil/gas as mentioned above as well as polymer flooding, alkali-surfactant-polymer flooding, and polymer-surfactant flooding. The capillary number is influential for chemical flooding because it is crucial in determining oil saturation.[9] A common way to represent this data is by using a capillary desaturation curve (CDC) (Figure 3). The CDC shows the pore arrangement within the media and fluid distribution within the pores. However, to produce a corresponding CDC to a data set one must first test the wettability effect of the solids involved which has an effect on the overall saturation (Figure 3). Wettability is one of the factors that contributes to relative permeability, which is effected by capillary number within a certain range.[4]
In terms of a microfluidic device, the use of rock and sand acts in a microfluidic way and can be developed into a controlled device. In the example provided here, uses a PDMS fabricated microfluidic device that was based on the geometry of sandstone. Oil is flooded through the system and in order to increase its contrast with the PDMS has been dyed with Sudan Blue, which is oil-soluble. The percent of oil remaining in the channel is calculated based on the flow rate of fluids such as water being passed through the device to obtain shear rate. This can also be measured as a function of capillary number versus the percent of oil remaining, where the closer capillary number approaches one the closer the percent remaining of oil reaches zero.
Relative permeability takes into consideration wettability as mentioned above, capillary end effects, geometry of the pore, rock type, and imbibition or drainage. It was found through experimentation by isolating wetting as the independent variable that at low capillary numbers capillary end effects had high influence. As a result, in order to produce consistently successful results for the relative permeability very high capillary numbers were achieved and monitored to ensure the capillary end effects did not become influential. These types of experiments show the just how important capillary number is to chemical flooding, especially when it comes to investigating relative permeability.[4]
Droplet Microfludics
Droplet formation is controlled by the formation and deformation of the liquid-liquid interface between the two immiscible phases. There are many forces which acts on droplet formation, but the most prominent among them is the capillary number.[10] The capillary number represents the ratio of viscosity to interfacial tension and with an increase in capillary number, there is a decrease in droplet diameter.[11] To be more specific, spherical droplets form at low capillary values and long liquid plugs at high capillary values (Droplet Microfluidics: T-Junction).
Squeezing, dripping, and jetting are other events that occur in droplet microfluidics. In the case of squeezing mode, low capillary numbers are used to produce droplets, in doing so a pressure gradient is formed across the droplet upon being formed. They droplets travel as plugs. In the case of dripping mode, viscous shear stress and interfacial tension compete as the capillary number increases with flow rate and the droplet fluid is broken up along its pathway through the channel. The droplets travel as small drips. Lastly, by increasing the capillary number and forces farther jetting occurs, resulting in droplets traveling as either spheres or plugs (Droplet Microfluidics: T-Junction).[12]
Capillary Valving
Capillary valves have been implemented frequently on CD fluidic platforms. The idea behind them is that they are controlled by surface tension, which occurs when the cross-section of the hydrophilic capillaries drastically expands. This expansion typically leads into a reservoir for the liquid to gather in. The pressure resulting from the rotation of the CD device increases the forces and capillary number in the channel.[13] As a result, the capillary valve can be overcome and droplets can form and progress into the larger expanded portion of the microfluidic channel. Based on the forces and capillary number affecting the fluid, this determines the potential of overcoming the forces of the capillary valve.[14]
References
- ↑ 1.0 1.1 1.2 Kantzas, A., Bryan, J., & Taheri, S. (n.d.). Capillary Number | Fundamentals of Fluid Flow in Porous Media. Retrieved February 23, 2018, from http://perminc.com/resources/fundamentals-of-fluid-flow-in-porous-media/chapter-2-the-porous-medium/multi-phase-saturated-rock-properties/dominance-capillary-forces-viscous-forces/capillary-number/
- ↑ Squires, T. M., & Quake, S. R. (2005). Microfluidics: Fluid physics at the nanoliter scale. Reviews of Modern Physics, 77(3), 977-1026. https://dx.doi.org/10.1103/revmodphys.77.977
- ↑ Gerbis, M., Gunter, W. D., & Harwood, J. (n.d.). Introduction CO2 capture and geological storage in energy and climate policy. Global CCS Institute, Retrieved February 23, 2018, from https://www.globalccsinstitute.com/archive/hub/publications/114711/building-capacity-co2-capture-and-storage-apec-region.pdf.
- ↑ 4.0 4.1 4.2 4.3 4.4 Guo, H., Dou, M., Hanqing, W., Wang, F., Yuanyuan, G., Yu, Z., Li, Y. (2017). Proper Use of Capillary Number in Chemical Flooding. Journal of Chemistry, 2017, 1-11. https://dx.doi.org/10.1155/2017/4307368
- ↑ Ding, M., & Kantzas, A. (2004). Capillary Number Correlations for Gas-Liquid Systems. Canadian International Petroleum Conference, 46(2), 27-32. https://dx.doi.org/10.2118/2004-062
- ↑ 6.0 6.1 Truby, J. M., Mueller, S. P., Llewellin, E. W., & Mader, H. M. (2014). The rheology of three-phase suspensions at low bubble capillary number. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 471(2173), 40557-40643. https://dx.doi.org/10.1098/rspa.2014.0557
- ↑ Ramakrishnan, T. S., & Wasan, D. T. (1986). The Relative Permeability Function for Two-Phase Flow in Porous Media: Effect of Capillary Number. Proceedings of SPE Enhanced Oil Recovery Symposium, 48(2). https://dx.doi.org/10.2523/12693-ms
- ↑ Nilsson, M. A., Kulkarni, R., Gerberich, L., Hammond, R., Singh, R., Baumhoff, E., & Rothstein, J. P. (2013). Effect of fluid rheology on enhanced oil recovery in a microfluidic sandstone device. Journal of Non-Newtonian Fluid Mechanics, 202, 112-119. https://dx.doi.org/10.1016/j.jnnfm.2013.09.011
- ↑ Zheng, B., Tice, J. D., & Ismagilov, R. F. (2004). Formation of Droplets of Alternating Composition in Microfluidic Channels and Applications to Indexing of Concentrations in Droplet-Based Assays. Analytical Chemistry, 76(17), 4977-4982. https://dx.doi.org/10.1021/ac0495743
- ↑ Jeong, S. (2005). Evaluation of the use of capillary numbers for quantifying the removal of DNAPL trapped in a porous medium by surfactant and surfactant foam floods. Journal of Colloid and Interface Science, 282(1), 182-187. https://dx.doi.org/10.1016/j.jcis.2004.08.108
- ↑ Tice, J. D., Lyon, A. D., & Ismagilov, R. F. (2004). Effects of viscosity on droplet formation and mixing in microfluidic channels. Analytica Chimica Acta, 507(1), 73-77. https://dx.doi.org/10.1016/j.aca.2003.11.024
- ↑ Ralf Seemann et al. (2012). Droplet Based Microfluidics. Reports on Progress in Physics, 75(1), 16-60. https://dx.doi.org/10.1088/0034-4885/75/1/016601
- ↑ Lepercq-Bost, E., Giorgi, M., Isambert, A., & Arnaud, C. (2008). Use of the capillary number for the prediction of droplet size in membrane emulsification. Journal of Membrane Science, 314(1-2), 76-89. https://dx.doi.org/10.1016/j.memsci.2008.01.023
- ↑ Madou, M., Zoval, J., Jia, G., Kido, H., Kim, J., & Kim, N. (2006). Lab on a CD. The Annual Review of Biomedical Engineering. https://dx.doi.org/10.1146/annurev.bioeng.8.061505.095758
