Brownian Ratchet/Deterministic Lateral Displacement - Matthew Tiller
Key Background Information
2nd Law of Thermodynamics
In order to discuss what exactly a Brownian Ratchet machine is, it is first important to be aware of and familiar with the Second Law of Thermodynamics.
This law states that entropy, or disorder per say, will always increase in a system that is isolated. Or that, at the very least, given a system that is ideal or is reversible, that the entropy will remain constant.
A good example of this is if you have two equal chambers separated by a semipermeable barrier with two different aqueous solutions. The components of one solution will diffuse across the barrier, increasing entropy within the overall system, until that component which can cross the membrane is at equilibrium on both sides of the barrier. The mixing of these two components reduces the order of the system.[7]
Brownian Motion
This is the process by which a particle in a medium can move in a random nature as a result of numerous kinetic collisions with surrounding particles.
Maxwell's Demon
A rudimentary thought experiment that is founded on the idea that you have a demon controlling a door between two equal chambers. One chamber has a mix of fast and slow particles. The other chamber is empty. As a fast particle approaches the door, the demon opens it to allow that particle to pass. Over time this implies that one chamber is predominantly filled with fast particles, and the other with slower particles. Initially this is fine, but later on as the 2nd chamber becomes filled with faster, higher-energy particles as the 1st chamber becomes lower energy, the entropy of the system decreases as the system becomes further and further from thermodynamic equilibrium which is a clear violation of the 2nd Law of Thermodynamics. [2]
Somewhat obviously however, the violation is rescinded if one accounts for the entropy of the demons actions by increasing the scale of the overall system to include the demon.
Brownian Ratchet Machine
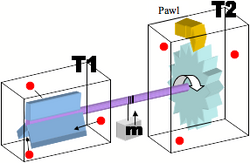
Such a machine is one that is theoretically capable of producing work from random variations that are a result of a heat bath that has no net flow of energy or mass. An image of the machine is shown below. The size of this machine is so small that the energy of a single molecule hitting the paddle wheel (the blue object in the T1 chamber) will be sufficient to rotate the system at least one notch on the ratchet and raising the the block that is tied to the axle in the process. The paddle wheel cannot spin backwards due to the pawl (the yellow object) and so clearly this starts to look like a classic example of a Maxwell Demon where the entropy of the system is decreased as the axle spins in only one direction based solely on the disorderly energy of the heat bath of T1. [3][4]
Ultimately, a Brownian Ratchet is something that appears to have a directional force induced by Brownian Motion despite its overall net force being zero.
Deterministic Lateral Displacement
This mechanism can be described briefly as an abstract sieve used to sort cells/molecules/etc. by their sizes that is only effective at low Reynolds numbers and with a specialized array of pillars within the channel.
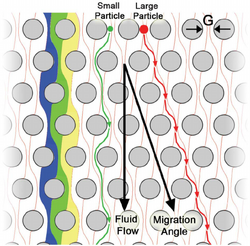
Often pillars/obstructions placed in a channel have little overall effect on the materials moving within that channel unless your intention is to mix them. However, when we start using more obscure pillar shapes or altering the arrays of those obstructions so that they are tilted (rather than having rows and columns that are perfectly horizontal and vertical), we can start to observe some interesting results. The first of which is the sieve nature, where the smaller materials are essentially unobstructed and continue with the flow, but the larger objects start to drift down a different direction despite the flow regime being uniform over the whole array. Most interestingly, this is exactly opposite of what you would expect to happen in regards to the entropy of the system, which would often prefer a thoroughly diffused mixture of materials. This is a result of the low Reynolds number creating a highly laminar flow that effectively prevents diffusing. In addition, the low Reynolds number has allowed us to reduce the Navier stokes equation
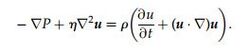
down to the Laplace equation
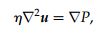
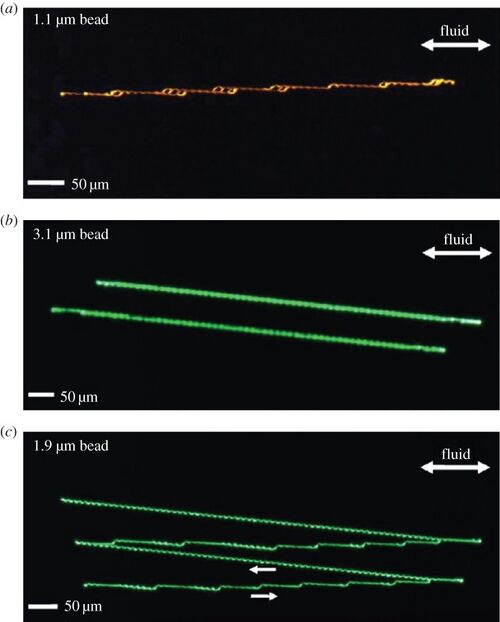
which has no time derivatives, and because of this, all of the flow paths becomes reversible. It is important to note however, that despite the flow being reversible, the non-hydrodynamic forces initiated by the collisions between the large materials and the obstructions causes the flow trajectories to be irreversible for some material sizes as is shown by the image below. [1][5][6]
A video displaying DLD and if you weren't already excited about witnessing the mechanism in action, the soundtrack featuring Carl Orff's Carmina Burana is surely gonna get you pumped up for this.
Uses of Deterministic Lateral Displacement
One of the uses for DLD is in the separation of larger objects such as cells from other components in the flow. It is entirely feasible to attempt to separate out metastasizing tumor cells which are noticeably larger than most other cells in the bloodstream. [6]
It can also be used for the isolation of smaller objects from the blood that are on a nanometer scale such as exosomes, which are otherwise exceedingly difficult to see or study.[6]
References
[1] Sturm J, Cox E, Comella B, Austin R. Ratchets in hydrodynamic flow: more than waterwheels. Royal Society Publishing. 2014, 4(6), (accessed Feb 17, 2017) [1]
[2] Leff H, Rex A. Maxwell's Demon Entropy, Information, Computing, Princeton University Press: Princeton. 1990 (accessed Mar 24, 2017) [2]
[3] Oudenaarden A, Boxer S. Brownian Ratchets: Molecular Separations in Lipid Bilayers Supported on Patterned Arrays. Science. 285(5430), 1046-048 (accessed Feb 17, 2017) [3]
[4] Ait-Haddou R, Herzog W. Brownian ratchet models of molecular motors. Cell Biochemistry and Biophysics. 2003, 38(2), 191–213 (accessed Feb 17, 2017) [4]
[5] Zeming K, Salafi T, Zhang Y & C. Asymmetrical Deterministic Lateral Displacement Gaps for Dual Functions of Enhanced Separation and Throughput of Red Blood Cells. Nature. 2016, 6 (accessed Feb 17, 2017) [5]
[6] Duffy S, Deng X, Tavasolli P, Black P. Technologies for label-free separation of circulating tumor cells: From historical foundations to recent developments. RSC Publishing. 2013, (accessed Feb 17, 2017) [6]
[7] Reckitt Benckiser. Why passive diffusion happens – entropy considerations. RSC Publishing. www.rsc.org/learn-chemistry/resource/download/res00000880/cmp00001061/pdf
