BioSysBio:abstracts/2007/Vinayak Doraiswamy

• Add or delete the sections that you require.

Computational Modeling of Chemotaxis in Cooperative Phenomena in Bacterial populations

Author(s): Vinayak Doraiswamy, Dr.Andrew Goryachev, Dr.Martin Buist
Affiliations: Graduate Programme in Bioengineering, National University of Singapore, Singapore; Centre for Integrative Systems Biology, University of Edinburgh, Edinburgh; Division of Bioengineering, National Univerity of Singapore, Singapore
Contact:email: vinayak@nus.edu.sg
Keywords: 'Bacteria' 'probabilistic models' 'Chemotaxis' 'Quorum Sensing'

Introduction

There has been considerable progress and advancement in computational cell biology and this has given researchers powerful tools to simulate metabolic, genetic and signal transduction networks. However there has been little development in designing computational tools to incorporate biologically realistic simulations of systems comprising many interacting biological cells. The necessity to model large ensembles of interacting cells commonly arises in the studies of disease pathology, cancer progression, embryonic development, wound healing and many other important biological processes, and in our case, bacterial quorum sensing.

Bacterial quorum sensing has become a very popular area of study in bacteriology. It is a phenomenon in which individual bacteria regulate gene expression by detecting changes in their population density. This is achieved by secretion and detection of auto inducer molecules, whose local concentration increase gives rise to altered gene expression. The ability of bacteria to congregate and reach the threshold density leads to this behavior. This ability might be because of bulk cell growth, or alternatively an efficient method for bacteria to achieve this is by chemotactic motion to form a congregate.

Aim of the Study

Our aim in this study is to first derive a model for bacterial chemotaxis that can take into account single cell dynamics and derive & describe the behavior of macroscopic transport coefficients like population velocity, diffusion coefficient etc. A single cell model that takes into account individual cell parameters like cell speed, chemotactic sensitivity, dissociation constant and give us a physiologically relevant model that can - account for single cell dynamics

- extract Population parameters and describe their behavior.

- be inserted into larger scale models on parallel computing platforms

- help predict convergence times to know behavior

- help us study the role of chemotaxis in cooperative behavior in bacterial populations

Outline of Methodology

Model:

We have derived a single cell level probabilistic model based on the cellular dynamics study by Frymer, that involves simulation of individual bacterial trajectories. The basic flowchart is given by

Fig.1. Flowchart of the simulation algorithm. The time delay is given to account for the time that the bacteria take to tumble (0.1s)

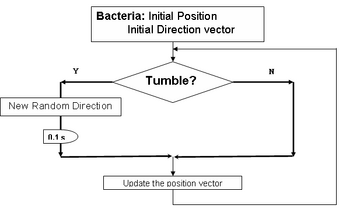
The crucial element in our model design is the tumbling probability(pt) term that causes the normal random-walk motion of bacteria to bias in the presence of a chemoattractant.

[math]\displaystyle{ Where, }[/math]

     [math]\displaystyle{  pt_0,  }[/math] is the basal tumbling probability in the absence of gradients
     [math]\displaystyle{  \chi\, }[/math]  is the chemotactic sensitivity coefficient
     [math]\displaystyle{ \nu\ , }[/math] is the velocity of the bacteria
     [math]\displaystyle{  K_d , }[/math] is the dissociation constant
     [math]\displaystyle{  \hat s\,  }[/math] is the direction vector
     [math]\displaystyle{  a , }[/math] is the concentration of the chemoattractant

Results: Unbiased Motion

The first simulation is performed in the absence of any chemo attractant. What we expect is a random walk similar to a Brownian motion of colloids. We do this to test the model and to find out the behavior of the parameters involved in the simulation.

Probability Density Function PDF: The probability density function of the bacterial population approaches a bivariate normal distribution at higher time values. As seen here in the figure, the pdf's at t=1s and t=100s.

Fig.2.Bacterial Probability density function at (a) t=1 seconds and (b)t=100 seconds. The density functions evolves to become a bi-variate normal distribution

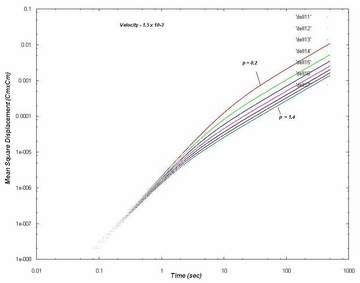
Mean Square Displacement(MSD): The mean square displacement vs. time curve on a log scale is show below. We expect it to behave in accordance with the Einstein’s relation for a random walk in a 2d plane which predicts a linear curve with the diffusion coefficient as the slope. We see the effects of stationary tumbling state on the rate of diffusion by varying tumbling probability.

Fig.3. Logscale plot of Mean square displacement versus time(500 seconds) for different values of tumbling probabilities from p=0.2 to p=1.4.

Covergence:

We observe that the bacterial population converges to diffusive behavior after a short period of time. To analyse this time of convergence, we use a Chi-Squared test and fit the radial bacterial displacement values to a Rayleigh distribution, and thereby extract the points of convergence. We find this pivotal point for various values of tumbling probabilities and bacterial velocities.

Fig.4. Time taken to converge to diffusive behavior versus the tumbling probability value (error bars indicate slight variations for different velocities). Overlaid plot of y= const/p

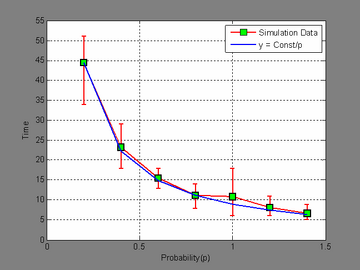
There is an inverse relation between convergence time and the tumbling probability with a scaling factor of 8.896. The run time therefore is proportional to the convergence time T. We can conclude that the bacteria tumbles 9 times before convergence. [math]\displaystyle{ T \sim\ 9 \times\ \tau\ }[/math]

Results: Gradient Field

A simple constant gradient was introduced along the x-axis to observe the resulting effects on the bacterial motion.

Dimensionless Trial: The problem was simplified by introducing two dimensionless variables, A & B, as follows:

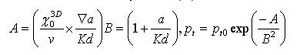
This was done to allow us to define a family of parabolic curves. Sets of these curves each define a behavior of the bacterial population with regards to the extent of skewing and value of convective velocities.

To better understand the population transport parameters, we simplify the problem to a single parameter. We observe that for the times we are looking at, the concentration values are very small, we can define a value epsilon such that

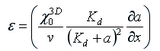
We can now vary this parameter (which in essence is varying the constant gradient field), and observe the change in behavior of the bacterial population.

Convective Velocity The convective velocity or the chemotactic velocity is the velocity with which the bacterial population moves as a whole in the direction of the gradient. In the results of the simulations, we take it as the rate at which the centre of mass is moving. Using the Berg & Brown equations, we have

[math]\displaystyle{ V_C = m \nu\ \tanh \epsilon\ \ }[/math]

The results of the simulation show that the chemotactic velocity approaches 0.9 times that of the bacterial velocity and also fit the curve given by the equation above.

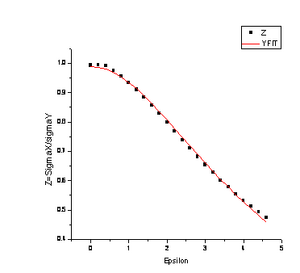
Diffusivity The diffusion along x and y axes are different in the presence of a gradient. The ratio of the diffusion coefficients is related to the epsilon value as follows:

[math]\displaystyle{ \mu\ = m \mu_0\ \cosh \epsilon\ \ }[/math]

This relation succinctly describes the change in diffusive behaviour for different gradients as seen here in a fit of the simulation curve with the hyperbolic function.

Fig.5. Plot of Ratio of standard deviations in x and y for different values of epsilon at t=400 seconds. Overlaid plot of y = sqrt (m*sech(n* ε)).

Cooperative Phenomenon in Bacteria

Under certain conditions, bacteria interact with each other by producing and sensing their own chemotactic signals. These signals include L-asparate, L-serine etc. There have been experiments demonstrating this behavior and formation of a quorum by this phenomenon. We aim to model this using our basic modeling framework.

The distinction in this phenomenon is that the chemoattractant gradient field is self generated by bacteria & therefore we need to account for the diffusivity of the attractant along with the bacterial diffusivity. The two basic equations for diffusion are thus given by:

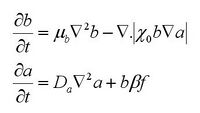
[math]\displaystyle{  Where,  }[/math]
     [math]\displaystyle{  b  }[/math]  is the local bacterial density
     [math]\displaystyle{  \mu_b\ , }[/math] is the bacterial diffusivity
     [math]\displaystyle{  a , }[/math] is the chemoattractant local concentration
     [math]\displaystyle{  \mu_a\,  }[/math] is the chemoattractant diffusivity
     [math]\displaystyle{  \beta\ , }[/math] is the metabolic coefficient that converts food f to self attractant a.

The concentration term in simulation protocol will now include the transient gradient given by the above equation.

Conclusion & Future Work

The current model describes bacterial motion in the presence of chemoattractant gradient. The population parameters compare very well with models from literature and we plan to test against other existing descriptions. We are incorporating this model into a large scale model that describes the complex cooperative phenomenon in bacteria like quorum sensing.

The advantage of single cell level model like ours is that it makes it possible for the model to be incorporated into larger systems like a parallel computational platform and define intracellular dynamics within that system using an agent based modeling technique. Further, this technique can be extended to other biological cells and also in cell-cell communication in multicellular organisms.

References

[1] Frymer,P.D., Ford,R.M., Cummings,P.T., 1993, Cellular Dynamics Simulation of Bacterial Chemotaxis, Chemical Engineering Science Vol 48, No.5, 687-699

[2] Berg,H.C. and Brown,D.A. 1972. Chemotaxis in Escherichia coli analyzed by three-dimensional tracking, Nature 239, 500-504.

[3] Park,.S. et. Al. 2003, Motion to form a quorum, Science, 301, 188.

[4] D.-J. Toh, F. Tang, T. Lee, D. Sarda, A. Krishnan, and A. Goryachev, Parallel computing platform for the agent-based modeling of multicellular biological systems. In: K. M. Liew, H. Shen, S. See, et al. (Eds.) Parallel and distributed computing: applications and technologies. (2004) Springer, Heidelberg.

For further help on editing, please see [ http://en.wikipedia.org/wiki/Help:Editing here]