BioSysBio:abstracts/2007/Vilda Purutcuoglu

From OpenWetWare

Jump to: navigation, search
  • Add or delete the sections that you require.

Bayesian Inference of a Realistic MAPK/ERK Pathway

Author(s): Vilda Purutcuoglu and Prof. Ernst Wit
Affiliations: Department of Mathematics and Statistics, Lancaster University
Contact:v.purutcuoglu@lancaster.ac.uk, e.wit@lancaster.ac.uk
Keywords: Bayesian inference, diffusion approximation, MAPK/ERK pathway, stochastic modelling

Features of the MAPK pathway

All cellular activations are regulated by various signal transduction pathways. The cellular signal transduction is the process of carrying over a signal in the cell's environment for producing an associate response [10]. This transfer is initiated by an external stimulus of the pathway by binding of an external protein to a receptor, and ends with the production of the target protein. The MAPK (mitogen-activated protein kinase) or its synonymous ERK (extracellular signal regulated kinase) pathway is one of the major signal transduction systems which regulates the cellular growth control of all eukaryotes including cell proliferation, differentiation, and apoptosis [6]. The activation of this pathway is triggered by an external stimulus of the growth factor EGF which binds to activated tyrosine kinase receptors and ends with the transcription and translation of the c-Fos gene [9].

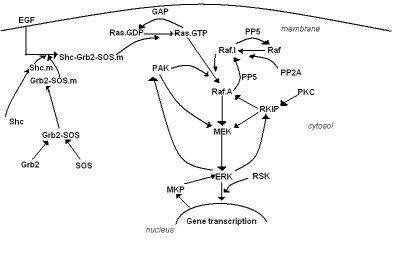
Image:Simple_MAPK_Figure_resized.jpg

(Figure 1:Simple representation of the structure of MAPK/ERK pathway)

The MAPK/ERK pathway has several organizational properties, which explain its complexity. The ultrasensitivity, the bistability, the periodic behaviour, and the existence of location-depended proteins are some of these characteristics [9]. On the other hand the structure of this mechanism whose main components are Ras, Raf, and MEK proteins (Figure 1), includes a number of phosphorylations on the protein level. The functionality of these proteins is stochastic in nature and directed by positive and negative feedback loops that cause either activation or inhibition of other proteins [9,6]. Due to the large number of interactions at the protein level, the outcome of the signaling is not a simple linear function of the signal. Interaction maps of the proteins or simple representation of the pathway like given in Figure 1 are not sufficient to exhaustively describe this complex system.

Representation of the pathway by quasi-reactions

Since the MAPK/ERK pathway is important in the cellular lifecycle, it has been intensively studied [8,5,6,1]. Some give a qualitative description of this regulatory mechanism [9,11]. However, none of the sources describe the system by an explicit set of reactions. We combine these qualitative sources for a representation of the pathway as a list of (quasi) reactions. We use multiple parametrizations to indicate different localization of the molecules in the cell and to describe the protein using different binding sites and various phosphorylations. The following set of equations, which describes the activation of the MAPK pathway by the EGF receptor, is part of the reaction list with 94 reactions and 51 substrates, representing 33 proteins and genes.

  • EGF + Shc \rightarrow EGF + Shcm (translocation)
  • Grb2 + SOS \rightarrow Grb2-SOS
  • EGF + Grb2-SOS \rightarrow EGF + Grb2-SOSm (translocation)
  • Shcm + Grb2-SOSm \rightarrow Shc-Grb2-SOSm
  • Shc-Grb2-SOSm + Ras.GDP \rightarrow Shc-Grb2-SOSm + Ras.GTP

Here, Grb2, SOS, Shc, EGF, Ras.GTP, and Ras.GDP are single proteins, Grb2-SOS and Shc-Grb2-SOS are protein complexes in the cytosol, and Shc-Grb2-SOSm is a protein complex near the membrane. As can be seen from the reactions, the translocation of substrates to the membrane is expressed by the notation m. For instance the protein Shcm denotes the Shc protein translocated from the cytosol towards the membrane. The different levels of the phosphorylation, on the other hand, are denoted by the index p or p1 and p2 where the first two abbreviations show the mono-phosphorylation and the latter implies the double-phosphorylation of a protein. For example, MEK.p2 represents the double-phosphorylated MEK protein on the S218 and S222 binding sites.

Modelling by diffusion approximation

Gene regulation is commonly modelled via ordinary differential equations (ODEs), which are based on the law of mass action and continuous concentrations of each chemical substrate. Although ODEs are successful to represent some reactions like linear production and degradation, they cannot describe the small system variability of the actual reactions. For biochemical systems, stochastic processes are a natural choice [2,12] as these kinds of dynamic formalization take into account the probabilistic manner of the different biological activations, such as the transcription of certain proteins, which occurs with low frequency in biological time [7].

In this study under the assumption that the probability distribution of the number of the molecules of each species at t depends on the continuous t and continuous number of molecules, we use the diffusion approximation to explain the change of state of each substrate at t. In this modelling the current state is found by a Langevin approach, where a correlated noise term describes the stochastic behaviour of the model over and above the drift term

dY(t)=\mu(Y,\Theta)dt+\beta^{\frac{1}{2}}(Y,\Theta)dW(t)

in which dW(t) is a s - dimensional vector representing the change of a Brownian motion over time and s is the total number of substrates in the system. \mu\,(Y_{t},\Theta)=V'a(Y_{t},\Theta) and \beta\,(Y_{t},\Theta)=V'diag\{a(Y_{t},\Theta)\}V are mean, or drift, and variance, or diffusion, matrices, respectively, both depending on the state of the system Y at time t, and the parameter vector \Theta=(\Theta_1,\Theta_2,\ldots,\Theta_r)^{\prime} explicitly. \Theta_{j}(j=1,\ldots,r) represents the stochastic rate constant of the jth reaction and r denotes the total number of reaction. Accordingly V is the net effect matrix and r-dimensional vector a\,(Y_{t},\Theta) describes the hazard of each reaction at time t. The algorithm computes the next state at t + dt by replacing Y(t) by Y(t) + dY [3,4].

Diffusion approximation for inference

For estimating the model parameters, i.e. the stochastic rate constants, we apply the discretized version of diffusion approximation, which is known as Euler approximation,

\Delta Y_{t}=\mu(Y_{t},\Theta)\Delta t+\beta^{\frac{1}{2}}(Y_{t},\Theta)\Delta W_{t}

where \Delta\ W_{t} shows a s-dimensional iid N(0,I\Delta\ t) random vector.

We define our data vector as a (n+1)x s matrix in which each column indicates a vector of Y_i=(Y_{t_0,i},Y_{t_1,i},\ldots,Y_{t_n,i}) and n stands for the total number of observed time step. Finally i is the indicator of the ith substrate.

Since the change in state for a given \Delta\ t has a multivariate normal distribution, the probability density function associated with this time increment is given by the following equation:

f(Y_{t+\Delta\ t}|Y_{t},\Theta):=N(Y_{t}+\mu(Y_{t},\Theta)\Delta t, \beta(Y_{t},\Theta)\Delta t)

f(Y_{t+\Delta\ t}|Y_{t},\Theta)=\exp ( {-\frac{1}{2}(\Delta Y_{t}-\mu(Y_{t},\Theta)\Delta t)'|\beta(Y_{t},\Theta)\Delta t|^{-1}(\Delta Y_{t}-\mu(Y_{t},\Theta)\Delta t)}\times(2\pi)^{-1/2}|\beta(Y_{t},\Theta)\Delta t|^{-1/2}


where \Delta\ Y_{t}=Y_{t+\Delta t}-Y_{t}. Then from equation above, we derive the likelihood as

L(Y|\Theta)=f(Y_{0}|\Theta)\prod_{i=0}^{n-1}f(Y_{t_{i+1}}|Y_{t_{i}},\Theta)

L(Y|\Theta)=f(Y_{0}|\Theta)\prod_{i=0}^{n-1}(2\pi)^{-1/2}|\beta(Y_{t_i},\Theta)\Delta t_i|^{-1/2}\times\exp ( {-\frac{1}{2}(\Delta Y_{t_i}-\mu(Y_{t_i},\Theta)\Delta t_i)'|\beta(Y_{t_i},\Theta)\Delta t_i|^{-1}(\Delta Y_{t_i}-\mu(Y_{t_i},\Theta)\Delta t_i))}

which is proportional to

L(Y|\Theta)\propto {\prod_{i=0}^{n-1}|\beta(Y_{t_i},\Theta)|^{-1/2}} \times\exp ( {-\frac{1}{2}\sum_{i=0}^{n-1}(\Delta Y_{t_i}-\mu(Y_{t_i},\Theta)\Delta t_i)'|\beta(Y_{t_i},\Theta)\Delta t_i|^{-1}(\Delta Y_{t_i}-\mu(Y_{t_i},\Theta)\Delta t_i))}

where Y_{t_i} shows the state of the ith substrate at time t.

As can be seen from the last expression of L(Y|\Theta\ ), the conditional posterior densities of reaction rates \Theta\ does not have a known distribution. We compute the posterior distribution of \Theta\ using the MCMC method. Under a symmetric candidate generator for each \Theta_j(j=1,\ldots,r), we apply a Metropolis-Hasting algorithm where the acceptance probability \alpha\ is found as follows

\alpha(\Theta,\Theta^{*}|Y)=\min ( {1,\frac{L(\Theta^{*}|Y)}{L(\Theta|Y)}})

in which \Theta\ ^{*} is the candidate value.

On simulated data the sampler converges well and is able to identify the dynamics of the MAPK/ERK pathway.

References

[1] L. Chang and M. Karin. Mammalian map kinase signalling cascades. Nature, 410(6824):37–40, 2001.

[2]N. Fedoroff and W. Fontana. Genetic networks: Small numbers of big molecules. Science, 297: 1129–1131, 2002.

[3]D. T. Gillespie. The chemical langevin equation. Journal of Chemical Physics, 113:297–306, 2000.

[4]A. Golightly and D. J. Wilkinson. Bayesian inference for stochastic kinetic models using a diffusion approximation. Biometrics, 61(3):781–788, 2005.

[5]J. J. Hornberg. Towards integrative tumor cell biology control of MAP kinase signalling. PhD thesis, Vrije Universiteit, Amsterdam, 2005.

[6]J. J. Hornberg, F. J. Bruggeman, H. V. Westerhoff, and J. Lankelma. Cancer: A systems biology disease. BioSystems, 83:81–90, 2006.

[7]D. A. Hume. Probability in transcriptional regulation and its implications for leukocyte differention and inducible gene expression. Blood, 96:2323–2328, 2000.

[8]W. Kolch. Meaningful relationships: the regulation of the ras/raf/mek/erk pathway by protein interactions. Biochemical Journal, 351:289–305, 2000.

[9]W. Kolch, M. Calder, and D. Gilbert. When kinases meet mathematics: the systems biology of mapk signalling. FEBS Letters, 579:1891–1895, 2005.

[10]E. Lawrence. Henderson’s Dictionary of Biology. Pearson Prentice Hall, 2005.

[11]B. Schoeberl, C. Eichler-Jonsson, E. D. Gilles, and G. M¨uller. Computational modelling of the dynamics of the map kinase cascade activated by surface and internalized egf receptors. Nature Technology, 20:370–375, 2002.

[12]T. E. Turner, S. Schnell, and K. Burrage. Stochastic approaches for modelling in vivo reactions. Computational Biology and Chemistry, 28:165–178, 2004.


Retrieved from "http://www.openwetware.org/wiki/BioSysBio:abstracts/2007/Vilda_Purutcuoglu"
Personal tools