BioSysBio:abstracts/2007/Stefano Lanzeni
- Add or delete the sections that you require.
Towards Metabolic Networks Phylogeny using Petri Net based expansional analysis
Author: Stefano Lanzeni, Enza Messina
Affiliations: Department of Computer Science and Communication, University of Milan-Bicocca
Contact:email: stefano.lanzeni@unimib.it, messina@disco.unimib.it
Author: Francesco Archetti
Affiliation 1: Department of Computer Science and Communication, University of Milan-Bicocca
Affiliation 2: CMR, Consorzio Milano Ricerche
Contact:email: archetti@milanoricerche.it
Keywords: 'metabolic networks' 'Petri Nets' 'Network phylogeny' 'Kullback-Leibler distance '
Abstract
Natural evolution acts on metabolism both at level of network functionalities and at level of single biochemical enzyme, breeding specificities in the metabolic network organization. Under an evolutionary point of view a reaction is integrated in a metabolism if and only if its substrates are made available by metabolic reactions in previous generations. Here we develop a novel approach, based on Petri Net, for simulating and analyzing the process of progressive network expansion. The method proceeds by seeding initially an arbitrary set of metabolites and incorporating new synthesized chemicals according to metabolic network structure. The proposed approach is applied on the well annotated metabolisms of red blood cells (Barrett et al. 2006), Escherichia coli (Honisch et al. 2004), Saccaromyces Cerevisiae (Duarte et al. 2004), Staphylococcus aureus (Becker & Palsson 2005), Mannheimia succiniciproducens (Hong et al. 2004) and Helycobacter pilory (Thiele et al. 2005). Results confirm the crucial evolutionary relevance of metabolic cofactors,and permit to characterize the usages of specific compounds among organisms. Given its ability in characterizing qualitative and qualitative differences between metabolisms our method ,used in association with proper measures of profiles similarity, could be thought of as a first step towards a network based philogeny.
Background
Petri nets constitute a mathematical formalism broadly used for modelling and analyzing discrete event systems with inherent concurrency (Petri 1962). They have shown to be suitable also to model biological systems (Pinney et al. 2002). A Petri net is represented by a bipartite graph [math]\displaystyle{ N=(P,T,I) }[/math], with [math]\displaystyle{ |P| }[/math] places, [math]\displaystyle{ |T| }[/math] transitions and [math]\displaystyle{ |I| }[/math] arcs connecting places with transitions and vice versa. Metabolic networks can be represented as a Petri Net [math]\displaystyle{ |N| }[/math] in which places are associated with metabolites and transitions to biochemical reactions. The structure of the Petri Net N is described by an incidence matrix [math]\displaystyle{ |S| }[/math] of dimension [math]\displaystyle{ (|P|,|T|) }[/math], also called Stoichiometric matrix, whose single element [math]\displaystyle{ s_{ij} }[/math] represents the stoichiometric coefficient of metabolite [math]\displaystyle{ i }[/math] in reaction [math]\displaystyle{ j }[/math]. We use Petri Nets for metabolic networks profiling with respect to specific environmental conditions characterized by the availability of certain compounds. The method is based on the concept of hierarchical ordering of metabolic reactions considered in (Handorf et al. 2005), which supposes that only those reactions may take place which could use available substrates, and these reactions produce new substances which may be used by further reactions. To capture these interdependencies we simulate and analyze the process of metabolic network expansion starting from arbitrary sets of biochemical compounds and progressively incorporating new synthesized compounds. We seed one or more metabolites in the network, then we search for the enabled reactions that lead to the synthesis of new chemicals. The process is iterated, breeding a process of network expansion, until no new compounds could be synthesised from the available metabolites. We denote as [math]\displaystyle{ scope }[/math] of a specific compound subset [math]\displaystyle{ x }[/math] ([math]\displaystyle{ scope(x) }[/math]) as the set metabolites that could be synthesized from the initial metabolites, in a non constrained number of reactive steps. For an extended mathematical description of the proposed algorithm, a more deep discussion on Petri nets, MatLab code and stoichiometric matrix of the considered organisms we remand the reader to our web site
Results
Role and ordering of metabolic co-factors

Metabolic co-factors are crucial biochemical compounds that act as a “currency”, since they are chemical energy carriers promoting exchanges of relevant functional groups needed in a large fraction of reactions. In order to investigate the different roles of these compounds in the considered metabolisms we computed the scope of each biochemical seeding initally also one co-factors set. In particular we considered five sets of co-factors: two sets respectively composed by {ATP, ADP, AMP} and {GTP, GDP} for energetic co-factors and by {NAD, NADH}{NADP, NADPH}, and {FAD, FADH2} for redox co-factors. Figure 1 reports the distributions of [math]\displaystyle{ scope }[/math] sizes ([math]\displaystyle{ |scope(x)| }[/math]) for all metabolites in the different metabolisms cited previously. Even if the biochemical mechanism of co-factors action is the same, each metabolism reacts to the introduction of specific co-factors sets in different ways. It is possible to qualitatively identify two groups of metabolisms: one in which the maximum and mean scope dimensions are obtained by seeding red-ox cofactors, and the other in which they are obtained by seeding energetic co-factors. According to the increase in the scope sizes it produces, each organism shows a specific ordering among co-factors sets, leading to a specific metabolic characterization. This finding suggests that, even if the biochemical action of a co-factor is the same in each life realm, its specific usage can be different, depending on environmental constraints and evolutionary pressures.
Profiling metabolic behaviours of biochemical compounds
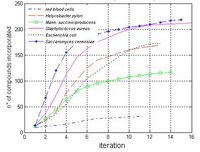
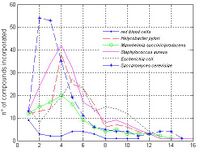
Our method has been used to characterize the usages of specific substrates in different metabolisms. At each step [math]\displaystyle{ t }[/math] of the network expansion process the method identifies the subset of metabolites [math]\displaystyle{ s(t) }[/math] that could be synthesized from the compounds available in the step [math]\displaystyle{ t-1 }[/math]. The information concering the size [math]\displaystyle{ |s(t)| }[/math] of each set [math]\displaystyle{ s(t) }[/math] could be used to derive absolute and relative profiles, describing both the total number of compounds progressively incorporated and the number of new compounds synthesized in each algorithm step [math]\displaystyle{ t }[/math]. In order to illustrate how to use our method in profiling metabolisms we simulated in each organism the process of network expansion seeding glucose as substrate, supposing that all the subsets of metabolic cofactors were initially available. The qualitative trend of the expansion process absolute profile, depicted in figure 2, is similar in all the metabolisms, with the exception of red blood cells, probably due to its little dimensions. Profiles are characterized by a rapid incorporation of compounds in the first iterations. In the terminal steps instead the size of the scope reach a saturation, since unavailable factors are required for the synthesis of novel compounds. The relative profiles, depicted in figure 3, show the relevance of each algorithm step, allowing the identification those steps in which a large number of compounds are synthesized because of the incorporation of critical compounds. The number of iterations required to reach critical compounds differs among organisms, and give an indication of the distance between the seeded compound and these metabolic hubs. The method proposed here may be used to characterize each organism in terms of “metabolic distances” among a benchmark of compounds. This requires the definition of a similarity metric between generated network expansion profiles based on the symmetric version of the Kullback-Leibler distance (Cover & Tomas 1991).
Conclusions
It is commonly recognized that natural selection acts on every structural entity of life, as it has been proven from the common practice that infers phylogenies based on the relationships among genomic and proteomic sequences. According to this observation it is plausible to suppose that also the structure of the biological network is selected through evolution, and we prospect phylogeny approaches based on networks comparisons. A fundamental element required for phylogenetic tree construction is the measurement of “similarity” among the biological entities that have to be correlated. For biological sequences local and global alignment algorithms give this information, leading to the inference of coherent evolutionary trees (Qi & Luo 2004). In the case of biological network comparison the situation is more complicated, because of a lack of techniques. The methodology we applied in this paper is in our opinion a first step in filling this gap, since it reveals some features relevant for compare systemic properties of entire metabolisms, like co-factors usage, nutrients catabolism and networks robustness. In this direction similarity metric between metabolisms based on the symmetric version of the Kullback-Leibler distance (Cover & Tomas 1991) among probability distributions, applied on the profiles obtained using Petri Net based network expansion, will be useful.
References
Barrett C L, Price N D, Palsson, B Ø (2006) Network-level analysis of metabolic regulation in the human red blood cell using random sampling and singular value decomposition. BMC Bioinformatics 7:132.
Becker S A & Palsson B Ø (2005) Genome-scale reconstruction of the metabolic network in Staphylococcus aureus N315: an initial draft to the two-dimensional annotation. BMC Microbiol 5(1):8.
Cover T M, Thomas J A (1991). Elements of Information Theory. John Wiley & Sons.
Duarte N C, Herrgard M J, Palsson B Ø (2004) Reconstruction and Validation of Saccharomyces cerevisiae iND750, a Fully Compartmentalized Genome-scale Metabolic Model. Genome Res 9: 1298-1309.
Handorf T, Ebenhoh O, Heinrich R (2005) Expanding Metabolic Networks: Scopes of Compounds, Robustness and Evolution. J Mol Evol 61(4): 498-512.
Hong S H, Kim J S, Lee S Y, In Y H, Choi S S, Rih J K, Kim C H, Jeong H, Hur C G, Kim J J (2004) The genome sequence of the capnophilic rumen bacterium Mannheimia succiniciproducens. Nature Biotechnol 22:1275-1281.
Honisch C, Raghunathan A, Cantor C R, Palsson B Ø, van den Boom D (2004) High-throughput Mutation Detection Underlying Adaptive Evolution of Escherichia coli-K12. Genome Res 14(12):2495-2502.
Petri, C.A. (1962) PhD Thesis, Institut fur Instrumentelle Mathematik, Bonn
Pinney J W, Westhead D R, McConkey G A (2003) Petri Net representations in systems biology. Biochem Soc Trans 31:1513–1515.
Qi J, Luo H (2004) CVTree: a phylogenetic tree reconstruction tool based on whole genomes, Nucleic Acids Res 32:W45-W47.
Thiele I, Vo T D, Price N D, Palsson B Ø (2005) An Expanded Metabolic Reconstruction of Helicobacter pylori (iIT341 GSM/GPR): An in silico genome-scale characterization of single and double deletion mutants. J Bacteriol 187(16): 5818-5830.