BioSysBio:abstracts/2007/Gabriela Kalna
- Add or delete the sections that you require.
Progression of oral carcinomas revealed by spectral reordering of a bipartite graph
Author(s): Gabriela Kalna, Keith Vass, Des Higham
Affiliations: University of Strathclyde
Contact:email: gabriela.kalna@strath.ac.uk
Keywords: 'spectral reordering' 'microarray' 'singular value decomposition'
Background/Introduction
Spectral, singular value decomposition-based, algorithms for dimension reduction and clustering are known to be useful in a range of areas of science and engineering. Motivation for this work is in the analysis of microarray data from a number of different samples leading to a natural bipartite graph framework. Spestral biclustering of microarray data was for the first time considered in [3]. In this work we generalize the ideas in [1] in order to present further theoretical support and illustrate the usefulness of the approach in an important application in cancer research.
We give a simple and informative derivation of a spectral algorithm for reordering weighted bipartite graphs with (a) positive and negative or (b) only non-negative weights. Thus, we attempt to identify sets of related genes and the corresponding samples in which the genes are (a) active or inactive or (b) behave uniformly. We start with a discrete optimization problem, then adding constraints relax it into a tractable continuous analogue. Natural data preprocessing is a part of the algorithm. Dominant singular vectors (the first in the case of positive and negative weights and the second in the case of non-negative weights only) can be used not only for reordering samples but also for identifying informative genes.
Results
Encouraging numerical tests of the graph bi-partitioning method on artificial test data and benchmark microarray datasets led us to an investigation of a complex picture of oral cancer progression that can be revealed from an multiclass dataset.
By current histopathological methods, it is impossible to predict prognosis of oral cancers and premalignancies in individual patients. There is an urgent need to be able to identify oral cancer subtypes and predict which premalignancies are most likely to progress to cancers.
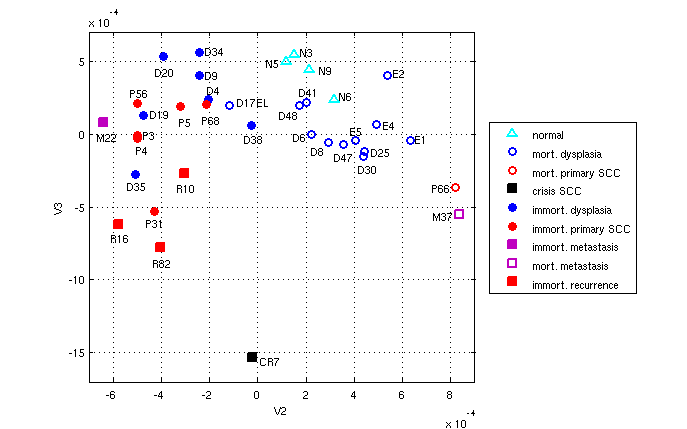
Application of the bi-partitioning algorithm to the overall gene expression profiles of different stages of head and neck cancer (dysplasias, primary oral cancers, metastases and recurrences) revealed a major distinction between two phenotypes, mortal and immortal, and indicated that the two oral cancer types use different mechanisms of invasion. Further, well known findings were confirmed as well as atypical samples were recognised by the algorithm. Two main types of premalignancy are well documented: erythroplakias and leukoplakias. Erythroplakias are much more likely to progress to cancer (marked E in the figure below, close to mortal cancers). Immortal erythroleukoplakias (D19, D35) and one immortal leukoplakia (D20), which later also progressed to cancer, show high similarity to immortal cancers. The immortal cancer P68 that clustered closest to the immortal leukoplakias is very atypical since it retains wild-type p53. Further details can be found in [2].
From the figure below, immortality is clearly a dominant factor influencing the overall gene expression profiles of both cancers and dysplasias. Genes consistently associated with immortality or differences between dyspasias and normal mucosa samples can be identified using dominant singular vectors.
Images/Tables
Materials/Methods
We consider first the problem
[math]\displaystyle{
\min \sum_{i=1}^M \sum_{j=1}^N (p_i - q_j)^2 w_{ij}
}[/math]
with [math]\displaystyle{ w_{ij}\gt =0 }[/math] and add the balancing constraints
[math]\displaystyle{
\sum_{i=1}^M p_i d_{gene_i} \approx 0
}[/math]
and
[math]\displaystyle{
\sum_{j=1}^N q_j d_{sample_j} \approx 0
}[/math]
to avoid the trivial solution where all genes/samples are put into a
single group. After relaxing, we impose the normalization constraints
[math]\displaystyle{
\sum_{i=1}^M p_i^2 d_{gene_i} =1
}[/math]
and
[math]\displaystyle{
\sum_{j=1}^N q_j^2 d_{sample_j} = 1
}[/math]
which damp down the influence of genes and samples with large overall
connectivity. Then we show that the new problem is solved by taking
normalized form of the first or second left and right singular vectors
of the matrix
[math]\displaystyle{
D_{gene}^{-1/2} W D_{sample}^{-1/2},
}[/math]
where [math]\displaystyle{ W }[/math] is the original gene expression matrix and [math]\displaystyle{ D_{gene} }[/math] and [math]\displaystyle{ D_{sample} }[/math] are fixed positive diagonal weight matrices.
Conclusion
The main aims of this study were to provide theoretical and algorithmic insight into graph bipartitioning based on the singular value decomposition and to apply these ideas in a cancer research setting. We showed that the algorithm is insensitive to the presence of outliers and can discover meaningful hidden patterns in the data. Results on the oral cancer multiclass dataset show the method is capable of revealing the whole picture of disease progression as well as detailed differences between its particular stages.
References
[1] D. J. Higham, G. Kalna and M. Kibble, Spectral clustering and its use in bioinformatics, to appear in J. Computational and Applied Math.
[2] K. D. Hunter, J. K. Thurlow, J. Fleming, P. J. H. Drake, J. K. Vass, G. Kalna, D. J. Higham, P. Herzyk, D. G. MacDonald, E. K. Parkinson,and Paul R. Harrison, Divergent routes to oral cancer, Cancer Res. 66, 7405-7413 (2006).
[3] Y. Kluger, R. Basri, J. T. Chang and M. Gerstein, Spectral biclustering of microarray data: coclustering genes and conditions, Genome Research 13, 703-716 (2003).
For further help on editing, please see here