BioSysBio:abstracts/2007/Daniel Mateus
Modeling Genetic Regulatory Networks from specified behaviors
Author(s): Daniel Mateus (1), Jean-Paul Comet (2), Jean-Pierre Gallois (1), Pascale Le Gall (2)
Affiliations: (1) CEA/LIST Saclay, France, (2) IBISC, université d'Evry, France
Contact:email: daniel.mateus at cea.fr
Keywords: 'Gene networks' 'Qualitative dynamical models' 'temporal properties' 'kinetic parameters'
Background/Introduction
Tools for modeling and simulation are needed to understand the functioning of genetic regulatory networks. The difficulty of determining the parameters of the models motivates the use of automatic methods able to find the parameters of the models whose dynamics match the behavior of the actual system. We propose a method applied on the qualitative modeling approach developed by R. Thomas. The logical parameters of the model, which are related to the kinetic parameters of a differential description, can be unknown. Translating the model into a symbolic transition system, and the known behaviors into temporal logic formulas, the method gives the constraints on the logical parameters corresponding to all the models having the specified behavior.
This work has been implemented in the AGATHA tool, which is also used in the validation process of industrial specifications [1, 2].
Models
The asynchronous and multivalued logical modeling of regulatory networks, which has been developed by R. Thomas and co-workers [3, 4, 5], generalizes the previously introduced asynchronous boolean modeling [6]. This generalized formalism has been used to model various gene networks.
A logical description is constituted of n variables, each representing the concentration of a constituent of the actual network, mainly the proteins produced by the genes of the network. Each variable xi can take an integer value between 0 and bi (bi is the maximum value of xi, and is less than or equal to the number of variables regulated by xi). A logical state E=(E1 ,…, En ) is a vector of values of the variables. With each state E, and each variable xi, is associated a logical parameter K(xi , E), which has an integer value between 0 and bi. The logical parameter is the value toward which the associated variable tends in the associated logical state. It means that in the logical state E:
- if K(xi , E)>Ei , then (E1 ,…, Ei +1,…, En ) is a successor of E;
- if K(xi , E)<Ei , then (E1 ,…, Ei -1,…, En ) is a successor of E;
- if K(xi , E)=Ei , for all i, then E is called a steady state, and has only itself as successor.
The graph of sequences of states is constituted of the logical states, and the transitions between each state and its successors.
Examples
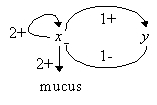
Pseudomonas aeruginosa are bacteria that secrete mucus (alginate) in lungs affected by cystic fibrosis, but not in common environment. As it increases respiratory deficiency, this phenomenon is a major cause of mortality in this disease. The simplified regulatory network, as proposed in [7], contains the protein AlgU (product of algU gene), and an inhibitor complex anti-AlgU (product of muc genes) (see figure 1. on the left: x stands for AlgU, y for anti-AlgU. The mucus production occurs when x=2).
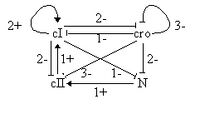
Bacteriophage lambda is a virus whose DNA can integrate into bacterial chromosome and be faithfully transmitted to the bacterial progeny. After infection, most of the bacteria display a lytic response and liberate new phages, but some display a lysogenic response, i.e. survive and carry lambda genome, becoming immune to infection. Figure 2. on the right is the graph of interactions described in [8] and involves four genes called cI, cro, cII and N.
The lytic response leads to the states (cI,cro,cII,N) is (0,2,0,0) or (0,3,0,0,) where cro is fully expressed. The lysogenic response leads to the state (2,0,0,0), where cI is fully expressed, and the repressor produced by cI blocks the expression of the other viral genes, leading to immunity.
In this two cases the logical parameters are unknown.
Methods
Given a constraint C on the logical parameters, and an initial logical state E, we generate a symbolic transition system (STS). Then the symbolic execution of the STS is made. This method constructs a tree of sequences of logical states, with the following rules:
- The root of the tree is the initial state E;
- For each possible successor of E, there can be a path constructed, if and only if the condition D on the logical parameters that makes a logical state E’ a successor of the initial state is compatible with C; then E’ is constructed, and an edge is constructed from E to E’;
- E’ is associated with a new constraint C’, which is the conjunction of C and D;
- The process is repeated with the successors of E’ and the constraint C’;
- If a new logical state has already been reached in the same path, then the execution of this path stops;
- The symbolic execution is over when all the possible paths have been treated.
We see that every state in the tree is associated with a constraint, which is called path condition, and is the constraint on the parameters which is necessary to the existence of the associated path in the logical model of the network.
To search a specific path in the symbolic execution tree we have adapted model-checking techniques for Linear Temporal Logic (LTL) [9]. A LTL formula expresses properties of a path. The method we use selects all the paths verifying the LTL formula, and synthesizes the disjunction of the path conditions associated with the last state of each path. The resulting constraint represents all the parameters compatible with the behavior specified by the formula.
Results
It has been observed that mucoid P. aeruginosa can continue to produce mucus isolated from infected lungs. The common explanation is that the mucoidy of P. aeruginosa is due to a mutation which cancels the inhibition of algU gene. But the hypothesis that this mucoid state occurs in reason of an epigenetic modification, i.e. without mutation, has been made [7, 10, 11]. With the method described here it is possible to find the constraints such that the resulting models has two stable behaviors, one mucoid (where x=2) and one non-mucoid (where x<2): 8 models are compatible with the epigenetic hypothesis.
In the case on lambda-phage, there are 2156 different models that have the following behaviors: lytic and lysogenic states are stable, and there is a pathway from initial state to lysis and to lysogeny. But in all these models, there is a common path to lysis, and one of two different paths to lysogeny.
Conclusion
Modeling genetic regulatory networks is generally confronted by the partial knowledge on the system: usually there is not only one model that is certainly accurate whereas the others are certainly false. Even with a qualitative formalism, different models can fit with experimental results. With our method, it is possible to manipulate not only one model, but a set of models compatible with experimental results. Then it is possible to verify if a hypothetic behavior is possible considering all the models (as the epigenetic modification in P. aeruginosa) or to see common behaviors over all the possible models (as possible pathways to lysis or lysogeny in lambda-phage); this kind of results is difficult to reach with only one complete model, as it is generally impossible to justify the unobserved behaviors it reveals. Moreover, by keeping a set of possible models, when a new behavior is discovered experimentally, the new result can be added to restrict the set of models, refining the knowledge on the system.
References
-
Bigot C, Faivre A, Gallois JP, Lapitre A, Lugato D, Pierron J Y, and Rapin N (2003). Automatic test generation with AGATHA. In TACAS, LNCS 2619, 591-596.springer
-
Gaston C, Le Gall P, Rapin N, and Touil A (2006). Symbolic execution techniques for test purpose definition. In Testing of Communication Systems, LNCS 3964, 1-18.springer
- ISBN:0849367662
- Thomas R, Thieffry D, and Kaufman M. Dynamical behaviour of biological regulatory networks--I. Biological role of feedback loops and practical use of the concept of the loop-characteristic state. Bull Math Biol. 1995 Mar;57(2):247-76. DOI:10.1007/BF02460618 |
- Thomas R and Kaufman M. Multistationarity, the basis of cell differentiation and memory. II. Logical analysis of regulatory networks in terms of feedback circuits. Chaos. 2001 Mar;11(1):180-195. DOI:10.1063/1.1349893 |
- Thomas R. Boolean formalization of genetic control circuits. J Theor Biol. 1973 Dec;42(3):563-85. DOI:10.1016/0022-5193(73)90247-6 |
- Guespin-Michel J and Kaufman M. Positive feedback circuits and adaptive regulations in bacteria. Acta Biotheor. 2001;49(4):207-18. DOI:10.1023/a:1014294120243 |
- Thieffry D and Thomas R. Dynamical behaviour of biological regulatory networks--II. Immunity control in bacteriophage lambda. Bull Math Biol. 1995 Mar;57(2):277-97. DOI:10.1007/BF02460619 |
- ISBN:0262032708
- Guespin-Michel JF, Bernot G, Comet JP, Mérieau A, Richard A, Hulen C, and Polack B. Epigenesis and dynamic similarity in two regulatory networks in Pseudomonas aeruginosa. Acta Biotheor. 2004;52(4):379-90. DOI:10.1023/B:ACBI.0000046604.18092.a7 |
- Bernot G, Comet JP, Richard A, and Guespin J. Application of formal methods to biological regulatory networks: extending Thomas' asynchronous logical approach with temporal logic. J Theor Biol. 2004 Aug 7;229(3):339-47. DOI:10.1016/j.jtbi.2004.04.003 |