BioSysBio:abstracts/2007/Alper Kucukural
Discrimination of Proteins Using Graph Theoretic Properties
Author(s): Alper Küçükural, Uğur Sezerman
Affiliations: Sabancı University
Contact:email: kucukural@su.sabanciuniv.edu
Keywords: 'Graph Theory' 'Bioinformatics' 'Delaunay Tesselation' 'Contact Maps'
Abstract
Graph theoretic properties of proteins can be used to perceive the differences between correctly folded proteins and well designed decoy sets. Graphs are used to represent 3D protein structures. We used two different graph representations of protein structures which are Delaunay tessellations of proteins and contact map graphs. Graph theoretic properties for both graph types showed high classification accuracy to discrimination of proteins. Fisher, linear, quadratic, neural network and support vector classifiers were used to classification of the protein structures. The best classifier accuracy was about %97.5. The results showed that characteristic features of graph theoretic properties can be used many fields such as prediction of fold recognition, structure alignment and comparison, detection of similar domains, and definition of structural motifs in high accuracy.
1 Introduction
Graphs are employed to solve many problems in protein structure analysis as a representation method[17, 19]. Contact maps are used for representation of 3D protein structures besides Delaunay tessellation of proteins. The aim of this paper is to find out properties to discriminate correctly folded proteins from misfolded artificial helices and well-designed decoy sets [3, 4] by the helping of graph theory. [7, 8]
11 different network properties of protein structures were calculated for further analyses with their averages and standard deviations of each protein.
First different feature selection methods such as principle component analysis are applied to determine the properties which have relative importance from others. Correlations of the properties are eliminated more fields. However the best results comprehend using with all the properties.
Classification and clustering methods are employed to decide the accuracy of the discrimination. In this paper we showed that graph theoretic properties can be used to differentiate the correctly folded protein structures from decoy sets in high accuracy which is very close to 97.5%.
2 Background and Related Work
Contact maps and Delaunay tessellated graphs are most common representation methods of 3D protein structures. If a protein consists of N residue, the contact map is an N×N matrix S. If the distance between Cα atoms for i. an j. residues in a protein smaller than 6.8 Aº [1], they are in contact and Si,j = 1 otherwise Si,j = 0. [2, 16] Delaunay tesselated graphs consist of partitions that are produced between a set of points. A point represented by an atom position in the protein for each different residue. This atom position can be chosen as α carbon, β carbon or the center of mass of the side chain. There is a certain way to connect these points by edges to have delaunay simplicies which form non-overlapping tetrahedral. [7] Delaunay tessellated graph includes the neighborhood information of these delaunay simplicies. When there are N residue in a protein, Delaunay tessellated graph is N×N matrix D. If two atoms in the protein such as i, j are neighbor according to Delaunay tessellation, Di,j = 1 otherwise Di,j = 0. Voronoi tesellation of proteins needs one step further process of Delaunay tesellation. Soyer et. al. reveal that Voronoi tesselation can be used for a representation method of folded proteins.[15]
Potential scores from averages of atom-atom contact preferences for each protein and graph theoretic properties were calculated for both types of graphs.
The definition of degree or connectivity k is the number of edges incident of a vertex or a residue i. [7] Average of the shortest paths between all the residues called characteristic path length L. These paths are also called geodesics. [9] Dijsktra algorithm is one of the fastest ways to calculate characteristic path length. [10] Determining weighted characteristic path length of a protein is made by the help of potential score matrices which are produced by Jernigan et. al. and Dill et. al. [5, 6]
Some classes have clustering property in the graph. Clustering coefficient measures this property. The clustering coefficient for each node Cn=2En / k (k−1), where En is actual edges of the residue n and k is the degree. The clustering coefficient of the graph C is the average of all the Cn. [7, 14]
Several measures are addressed to discover the centrality of a node in a graph. Betweenness, clossness, stress and graph centrality measures count as standard measures of centrality.[11, 20] If the centrality measure of a node is high, this node has a central role in the structure of a protein and can be crucial its folding. [7]
An atom-atom contact scoring function was applied by McConkey et. al. on delaunay tesselated protein structures to make comparisons with decoy sets. They can correctly identify the native proteins, if contacts are in quaternary structures with their scoring function. However the results in subunits of the proteins are not satisfactory. [3]
Another density based scoring function was formed by Wang et. al. to distinguish native, correctly folded protein structures from decoy sets. Their function was based on to calculate Root Mean Square Deviation (RMSD) between all Cα atoms in a given decoy set. The success rate of this function was about 90%. [4]
Taylor et. al. stated that limited ability to distinguish proteins using network properties on delaunay tessellated graphs.[7]
Another research by Gatchel et. al. declared the correlation coefficient between RMSD and free energy and minimum discriminatory slope (MDS) together provide much more information about discrimination of native proteins from decoy sets. [12]
Hydrophobic effect on protein folding and its importance to discrimination of proteins were stated by Fain et. al. Their scoring function was based on Z-Score optimization and the Chebyshev expansion of the potential scores. [13]
Classification, clustering methods such as neural network based approaches and support vector machines are widely used in differentiation analysis and structure prediction of proteins. [16, 21, 22] Prediction accuracy of T.N. Petersen et. al is up to 80%. [18]
3 Datasets
First data set in three which is from PISCES has 1364 non-homologus proteins, and their resolution < 2.2Å, crystallographic R factor < 0.23, and maximum pair wise sequence identity < 30%. Second data set consists of 1364 artificially generated and well designed decoy set and the third one is 101 artificially generated straight helices. [7, 23]
4 Experimental Methods
Produced graphs for both types of representation methods that are Delaunay tessellation and contact maps are used for the calculation of some of the graph theoretic properties shown in Table 1. for all the datasets. Delaunay tessellated graphs were produced by Qhull program. [24] Averages and their standard deviations are calculated for each protein. These values are employed as dimensions of the classification methods. Than pair wise correlation table are calculated to eliminate one of the highly correlated features. Feature selection methods are used such as backward, forward and principle component analysis to discover the principle components. Classification methods are used to find out whether the graph theoretic properties can discriminate the native proteins or not.
Table1. Abbreviations of graph theoretic properties and potential scores
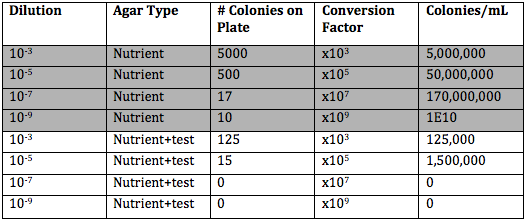
5 Results
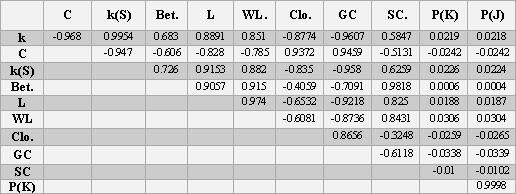
Classification results are obtained from PRTools. [22] The results from Delaunay tessellated graphs are given in Table 2. a-d and Contact map results are given in Table 3.a-d. Although the results were produced by 10 different classification methods, it is given 4 classifier results which have minimum classification error. Pairwise correlations of graph theoretic properties given in Table 4.br>
Table 2. Results from the Delaunay Tessellated Graphs
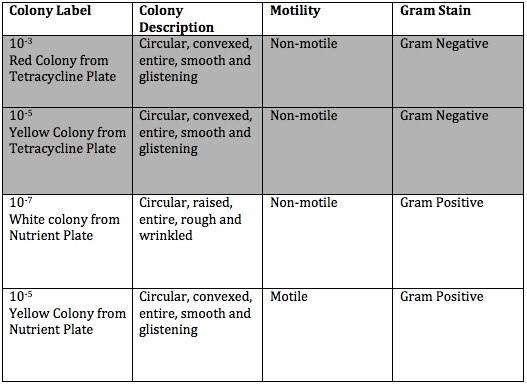
Table 3. Results from the Contact Maps
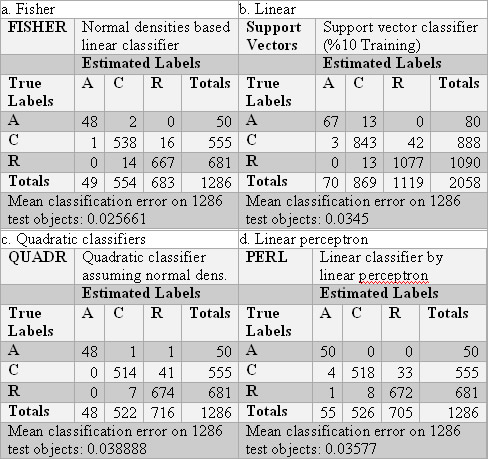
Table. 4. Pairwise correlations of graph theoretic properties.
6 Conclusions
All of the feature selection and principle component analysis methods gave high importance to characteristic path length, weighted characteristic path length and theirs standard deviations. As long as there are highly correlated properties, any feature selection and elimination methods reduced the accuracy of the results. The discrimination features of standard deviations are higher than the averages. As far as graph types are concerned, the classification accuracy rates of the contact map graphs are higher for the results of the same classification methods. Stress centrality results have much more importance of the other centrality methods according to PCA results.
In conclusion, graph theoretic properties which were mentioned in this paper can be used to differentiate the correctly folded proteins in very high accuracy.
7 References
1. A. R. Atilgan, P. Akan, C. Baysal, "Small-World Communication of Residues and Significance for Protein Dynamics," Biophys. J., 86, 85-91 (2004)
2. Vendruscolo, M., E. Kussel, and E. Domany, Recovery of Protein Structure from Contact Maps. Structure Fold. Des., 1997. 2:p.295-306.
3. McConkey, B.J., Sobolev, V., and Eldman, M. 2003. Discrimination of native protein structures using atom–atom contact scoring. Proc. Natl. Acad. Sci. 100: 3215–3220.
4. Wang K., Fain B., Levitt M., Samudrala R. Improved protein structure selection using decoy-dependent discriminatory functions. BMC Struct. Biol. 2004;4:296.
5. Miyazawa, S. & Jernigan, R. L. (1996) J. Mol. Biol. 256, 623–644.
6. Liang, J.and K.A. Dill, Are proteins Well-Packed? Biophys, J.,2001. 81:p. 751-766.
7. Taylor T., Vaisman I.I. (2006) Graph theoretic properties of networks formed by the Delaunay tessellation of protein structures. Phys. Rev. E. Stat. Nonlin. Soft. Matter Phys.: 73: 041925
8. Alper Küçükural, Uğur Sezerman, Finding Common Domains of Proteins Using Parallelized Attributed Inexact Sub-graph Matching Algorithm, TAM 2006.
9. L. Freeman, Sociometry 40, 35 _1977_.
10. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 24.3: Dijkstra's algorithm, pp.595–601.
11. Ulrik Brandes (2001) A Faster Algorithm for Betweenness Centrality. Journal of Mathematical Sociology 25(2):163-177. 2001.
12. Gatchell D, Dennis S, and Vajda S. Discrimination of near-native protein structures from misfolded models by empirical free energy functions. Proteins, 41: 518-534, 2000.
13. Fain B, Xia Y, Levitt M. Determination of optimal Chebyshev expanded hydrophobic discrimination function forglobular proteins. IBM J Res Dev 2001; 45:525-532.
14. M. Vendruscolo et al., Phys. Rev. E 65, 061910 2002.
15. Soyer, A., J. Chomiller, J.-P. Mornon, R. Jullien, and J.-F. Sadoc, Voronoi Tesselation Reveals the Condensed Matter Character of Folded Proteins. Phys. Rev. Lett., 2000. 85:p.3532-3535.
16. Fariselli, P. and R. Casadio, A Neural Network Based predictor of Residue Contacts in Proteins. Protein Eng., 1996. 9:p.941-948.
17. Strogatz S.H.,Exploring Complex Networks, 2001.410:p.268-276.
18. Petersen, T.N., C. Lundegaard, M. Nielsen, H. Bohr, S. Brunak, G.P. Gippert, and O. Lund, Prediction of Protein Secondary Structure at 80% Accuracy. Proteins,2000.41:p.17-20.
19. Albert, R. and Barabasi, A.-L., Statistical mechanics of complex networks, Rev. Mod. Phys. 74, 47–97 (2002).
20. A Measure of Betweenness Centrality Based on Random Walks, M. E. J. Newman, DOI: cond-mat/0309045, arXiv, 2003-09-01.
21. Zhao, Y., Karypis, G.: Prediction of contact maps using support vector machines. In: Proceedings of the IEEE Symposium on BioInformatics and BioEngineering, IEEE Computer Society (2003).
22. Ferdi van der Heijden, Robert P.W. Duin, Dick de Ridder and David M.J. Tax, John Wiley & Sons, Classification, parameter estimation and state estimation - an engineering approach using Matlab, 424 pages, ISBN 0470090138, (2004).
23. G. Wang and R. L. Dunbrack, Jr., Bioinformatics 19, 1589, (2003).
24. C. B. Barber, D. P. Dobkin, and H. Huhdanpaa, ACM Trans. Math. Softw. 22, 469 (1996).