Ashley Rhoades Week 2
Chemostat Model
Part 1: Nutrient/Cell Population Model
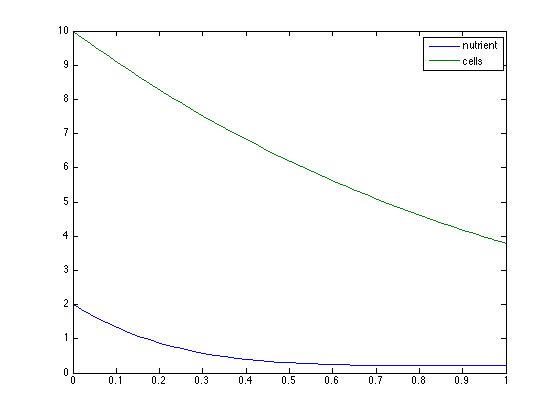
In this model the inflow rate, concentration inflow, growth rate, saturation, and consumption are all parameters. The dependent variables are the nutrient concentration and cell population and these are functions of time. There is one differential equation for the change in the nutrient concentration and one for the change in cell population over the change in time. By putting the differential equations into MATLAB the cell population and nutrient concentration can be observed given different parameters. For this first model I played with the five parameters mentioned earlier. After inputting different values I wanted to see what each parameter did to the cell population and nutrients when increased dramatically, while keeping the other parameters constant. The base values I used for each was 1 and for the consumption rate(or waste production) it was 0.1. When I changed the inflow rate from 1 to 10 I observed that the cell population approached zero and the nutrient levels increased. This result was more apparent when I increased the inflow rate to 100 volume units per unit time. Because we are at a constant volume in the chemostat this makes sense because inflow increasing the outflow and the cells aren't growing fast enough to maintain their population.The image below shows the plot before any parameters were changed.
Next when I changed the nutrient concentration of the inflow the nutrients slowly surpassed the cell population. Then when I put 100 of some concentration units in for the inflow concentration the cell population again did not change but the nutrient population sky rocket. Since there's only so many cells with the other parameters like population growth rate are low the cell population cannot grow much even with nutrients increased. So when I did dramatically increase the growth rate, and left the other values low, the nutrient levels dropped to zero. The level of saturation of nutrients had little effect of the cell population and nutrient levels.
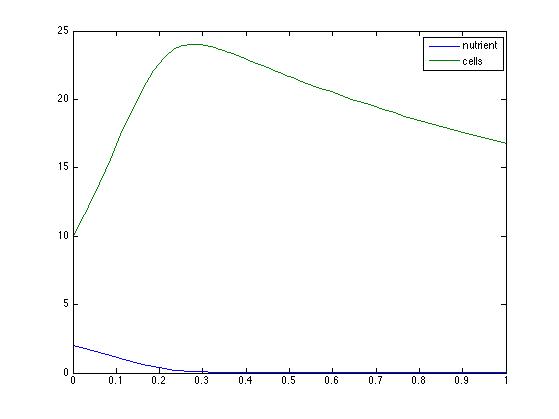
Since the consumption rate started at only 0.1 I just rose it to 2 and then 10. With the increase to 2 the cell population increased and then began falling, in accordance with the minimal nutrients available. When I raised it to 10 the bump in the cell population is more exaggerated and the nutrient levels drop quickly as seen in the image below.
Part 2: Logistic Growth Model
This model factors in the carrying capacity of the population. Overall increasing each parameter from 1 to 10 to 100 with the exception of the consumption rate( that was increasing from 1 to 2 to 10) yielded similar results to the earlier model. The graph with all the parameters for this model looks very similar to the first image above.
Again increasing inflow rate sent the cell population to zero and the nutrients increases to a steady level. A dramatic increase in nutrient concentration of the inflow, with other parameters constant, did not change the cell population but the nutrients skyrocketed. When the growth rate was increased to 10 instead of 1 a slight hump in the cell population growth was visible, showing a moment of population growth before the nutrients were quickly gone. Again with all other parameters constant saturation seemed to have little affect on the system. The consumption rate increase showing a dramatic hump in the cell population mirroring the decrease of nutrients levels.
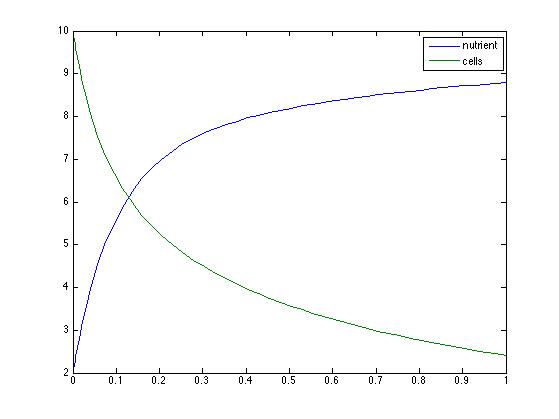
Because my results were very similar I played around with the parameters a little more. I found that when I increased all parameters the cell population and nutrient levels crossed over each other as can be seen below.
Suggestions
As far as my suggestions for this models, I feel that knowing more information about the behavior of the yeast would be helpful. This would allow the parameters to be realistically adjusted. For example, maybe yeast has a certain range of growth rate or waste production. Then the parameters can be manipulated within the ranges. It would be interesting to look at the nutrient solution as well. Yeast can react differently with each nutrients. Also, if the yeast is using up nutrients and producing waste the waste could be performing reactions with the nutrients solution. Knowing the chemical reactions occurring in the chemostat could add significantly to the success of the model.