20.309:Homeworks/Homework2
Introduction
Here we will look at power spectra in matlab, and some issues associated with discrete-time Fourier analysis. You should save your matlab code in an m-file, which will make it easy to modify and reuse it, and submit your m-file along with your plots.
Remember, when in doubt about any of the matlab commands given below, use the help command to get info about how to use each one - the Windows installation of matlab will have this same info and more accessible via the Help menu.
Matlab command for computing power spectra is pwelch. To get a feeling of what pwelch
does, here is a diagnostic problem and answer to the problem associated with the command. Try
problem 1 in the problem section first, and then come back to the diagnostic problem. It is
also beneficial to take a look at the Matlab help page for pwelch for its input and output arguments
and other detailed information as you read through this section.
1.1 Diagnostic problem
An important feature of pwelch is that it always correctly normalizes the total power of the PSD,
but - depending on the parameters you use|you can get quite different PSD shapes for the same
signal. For example, the default parameters give a lot of spectral leakage. To see a low-leakage
spectrum, try running pwelch with the nfft and window parameters satisfying the following conditions:
- the sinusoid frequency f_SIN is an integer multiple of the quantity fsamp/Nfft
- window is the same length as nfft.
Can you suggest what causes spectral leakage? Plot the low-leakage PSD on the same axes as your previous linear and log plots (use hold after plotting one waveform to freeze a figure, before plotting a second). Considering the relative magnitudes, how much does the leakage matter?
1.2 Answer
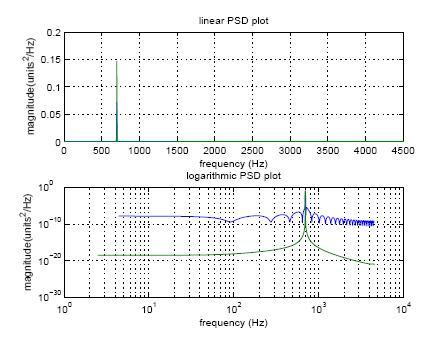
(See Figure on next page.)
In order to get a low-leakage PSD, the distribution of FFT points along the frequency axis must be such that one of the points exactly coincides with the frequency of the sinusoid. Leakage happens when signal power exists at frequencies between those represented by FFT points. Since, in practice, this happens anytime you don't know precisely what the input function is (and if you do, there's no point in measuring its spectrum), leakage is seen. Being aware of it, and knowing how it can be reduced is important.
There are Nfft points in a PSD computed by pwelch, which are distributed evenly through
the region of the spectrum between -fsamp=2, and fsamp=2 (the positive and negative frequencies
are then combined for a one-sided PSD, since the FFT of real signals is symmetric) therefore Nfft
must be chosen to obey
f_SIN = k*(fsamp/Nfft), [k = 1,2,3,...].
In other words, the frequency of the sinusoid needs to be an integer multiple of fsamp/nfft. Of
course, nfft should be large enough to give a decently tight spacing of points in the PSD.
Problems
1. Use matlab to generate a time vector y(t), approximately one second long, with a sampling frequency fsamp of a few kHz (the syntax "vector=start_value:increment:end_value;" will be useful here - increment is the time between your samples or 1/fsamp). Then create a sinusoid based on that time vector - choose a frequency fSIN of a few hundred Hz:
y = sin(ω_SINt) = sin(2πf_SINt)
Calculate the PSD of your sinusoid using the pwelch (1) command, and plot it on a linear scale and a logarithmic scale; use the plot and loglog commands, respectively. What is the significance of the highest and lowest frequencies that appear on the plot?
2. Recall that one of the consequences of Parseval's theorem is the following relationship between
a time-domain signal f(x) and its PSD F(ω):
<f(x)^2> = ʃF(ω)dω.
Verify that this is the case for the sine wave you've been using by computing its mean-square
value in the time domain, and the integral of its PSD in the frequency domain (matlab's
var and sum functions will be useful here). Remember that you're effectively calculating an
area, and make sure that units match up: pwelch gives you the PSD in units^2/Hz, while the
integral of your PSD needs to be equal to a mean-square value (units^2).
3. Now use the randn command to generate a noise signal with the same length as your time
vector. Calculate its PSD with the pwelch parameters of your choice, and plot it on a new
log plot. To observe the benefits of averaging, generate a noise signal that is 10× longer in
duration, calculate its PSD, using the same pwelch parameters, and plot its spectral density
on the same plot.
4. Take the sinusoid from problem 1, but with its amplitude reduced tenfold, and the first
(short duration) noise signal from problem 3, and add them together. Look at a section of
the summed waveform in the time domain - can you find the sine wave at all? Now plot the
PSD of the combined signal - can you find the sine wave peak in the noise? What can you
do to get it to resolve more clearly? (Problem 3 should provide a clue.) Plot your result on
the same axes.
5. (BONUS) Finally, take the original sinusoid from (a), compute its Discrete Fourier Transform using the fft command, and plot its magnitude (an FFT is complex-valued) on a
semi-log plot (see the semilogy command). Compare this to the PSD of the sine wave given
by pwelch, and comment on the FFT's features: Why two peaks? What is the meaning of
its x-axis values? Why are the values along the y-axis so large?
__________________________
1The syntax is [PSDvect, freqvect]=pwelch(signal,window,n overlap,nfft,f samp) and only requires you to
supply a signal vector and a number for f_samp to properly scale and calculate the frequencies for the PSD { i.e.
pwelch(signal,[ ],[ ],[ ],fsamp) will get you a result. The result is stored in the two vectors before the = sign.
Use matlab's help</code< to find out what the other parameters do. For parameters that you leave out by entering "[ ]",
matlab uses its defaults (also found in help).