20.181/Lecture8
FAQ
Probability of a tree
- How do we get from what we know (score of data given a tree) to what we want (score of the tree, given the data)?
- [math]\displaystyle{ P(T|D) \rightarrow P(D|T) }[/math]
- From last time, one of the assumptions that we made is that without knowing anything about the data, two trees (T1 and T2) are equally likely.
- [math]\displaystyle{ \frac{P(T_1|D)}{P(T_2|D)} = \frac{P(D|T_1)P(T_1)}{P(D|T_2)P(T_2)} }[/math]
- Note: when we propose a tree, we'll also find the branch lengths that work best for that tree. We'll treat that as part of the topology.
- Expression for the joint probability of all data:
- [math]\displaystyle{ P(D|T) = P(A,C,C,C,G,x,y,z,w|T) }[/math]
- T = topology of the tree (includes t1,t2... all the branch lengths)
- We're going to refer to x,y,z,w as "nuisance parameters"
- We don't care what their values ARE, we're just going to try ALL of them, and just integrate through.
- Join probability of the data can be separated into each of the independent events (mutations), and the probability of each event is exactly what the J-C formula gives us the way to calculate!
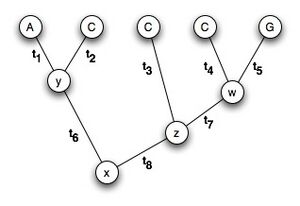
- [math]\displaystyle{ P(A,C,C,C,G,x,y,z,w|T) = P_x*P_y*P_z*P_w }[/math]
- [math]\displaystyle{ P(x) = P_x }[/math]
- [math]\displaystyle{ P(y|x, t_6)*P(A|y, t_1)*P(C|y, t_2) = P_y }[/math]
- [math]\displaystyle{ P(z|x, t_8)*P(C|z, t_3) = P_z }[/math]
- [math]\displaystyle{ P(w|z, t_7)*P(C|w, t_4)*P(G|w, t_5) = P_w }[/math]
- Now that we have an expression for the joint probability, we can sum over the nuisance paramaters. For each possible set of values for the nuisance parameters, the joint probability distribution will take on a particular value. We then ADD these because we don't care what the nuisance parameters' values are, they can be one set of values, OR another set of values, OR another set of values ... (each sum is over the 4 possibilites ACGT)
- [math]\displaystyle{ \sum_x\sum_y\sum_z\sum_w P_x*P_y*P_z*P_w }[/math]
Marginalizing
In order to calculate
- [math]\displaystyle{ \sum_x\sum_y\sum_z\sum_w P_x*P_y*P_z*P_w }[/math]
- Now consider that:
- P_x doesn't depend on y or z or w,
- P_y doesn't depend on z or w,
- P_z doesn't depend on w,
- but P_w depends on x and z.
- You can pull terms in front of the sum if they don't depend on the variable you're summing over.
- [math]\displaystyle{ \sum_x P_x\left(\sum_y P_y\left(\sum_z P_z\left(\sum_w P_w\right)\right)\right) }[/math]
- When you're considering the likelihood at a partcular node ([math]\displaystyle{ P_x }[/math] for example) you have to look at 64 possibilities (4 at parent, 4 at each child)
For p in ACGT:
- For q in ACGT:
- For r in ACGT:
- [math]\displaystyle{ P = P(q) * P(r) * P(q|p,t_{pq}) * P(r|p,t_{pr}) }[/math]
- L[p] +=P
- Note:
- P is probability
- p is the state of the parent node (ACGT)
Designing an Algorithm
Remember Fibonacci!
remember Fib:
- return kth number
- return series
- the series was the smart way to do it- the other one explodes computationally
Efficient computation
In the Sankoff algorithm presented in class, we did this by simply calling this whole function again (64 times)- this will work, but it could be VERY expensive for anything but the smallest trees. Fortunately, there is a better way...
The problem is that we included the recursion in a loop, so it is called many times for each node:
def sankoff(tree,nodeSeq): #this function returns the score for a particular state at the root
- min = inf #initialization
- if tree is a leaf: #stop condition
- if tree['data'] == nodeSeq:
- return 0
- return inf
- for leftSeq in [A,C,G,T]: #now we're at a node with two children
- for rightSeq in [A,C,G,T]: #we have to try all 16 possibilities here
- sum= cost(nodeSeq,leftSeq,rightSeq) #cost is some function that looks up the cost in the table
- sum += sankoff(tree['left'],leftSeq) #we have to remember to pass the cost along!
- sum += sankoff(tree['right'],rightSeq)
- if (sum < min):
- min = sum
- return min
...but we can move the recursion out of the loop if we return the costs for each possible nucleotide at each node
def sankoff(tree): #this function returns a dictionary of scores for all possible states at the root
- for parentSeq in [A,C,G,T]: #initialization
- scores[parentSeq] = inf #infinity
- if tree is a leaf: #stop condition
- if tree['data'] == nodeSeq:
- scores[tree['data']] = 0 #every state except the observed is set to infinity
- return scores
- leftScores = sankoff(tree['left']) #recursion moved outside of loop
- rightScores = sankoff(tree['right'])
- forparentSeq in [A,C,G,T]: #try all seqs at the current node
- for leftSeq in [A,C,G,T]: #now we're at a node with two children
- for rightSeq in [A,C,G,T]: #we have to try all 16 possibilities here
- sum = cost(nodeSeq,leftSeq,rightSeq) #cost is some function that looks up the cost in the table
- sum += leftScores[leftSeq] #we have to remember to pass the cost along!
- sum += rightScores[rightSeq]
- if (sum < scores[parentSeq]):
- scores[parentSeq] = sum
- return scores #return the dictionary
Note that this is exactly what we did with the fibonacci function to prevent unnecessary recursion - we returned a list of values instead of a single case. This is the dynamic programming approach: efficiently break a problem up into independent (and non-redunant) subproblems.
OK... now to apply these lessons to a maximum likelihood computation:
We want to define a function outside our main loop, and we want it to grab the probabilities P(q) for all q in ACGT P(r) for all r in ACGT
where q is state at the left subtree, and r is state at the right.
To do this we'll need a function that returns the probabilities for all possible states. For example:
def ml(tree,pos):
- (insert code here)
- return {'A':0.1,'C':0.2,'G':0.1,'T':0.1} #values are just as an example!
- This is the trick we really want to see you implement in HW5; this is where dynamic programming comes in.
- We're not going to compute these probabilities 64 times.
- Recall how we pulled terms out of the sum.... we can take advantage of that to break up the problem in an intelligent way:
- Separate computation of P_w which doesn't depend on x,y,z
- Separate computation of P_z which doesn't depend on x,y
- ...etc...
Some additional hints: in Sankoff, we took the min of the scores, but here we want to ADD all of the possible probabilities for each possible state of the internal nodes. Also, our cost function here is a function of time(distance), so we wont just look it up in a tablew. We have a separate function to calculate the probability under the Jukes-Cantor model of evolution.
Greedy Algorithm for trying trees
- A heuristic (contrast with dynamic programming)
- We give up and say we're not going to find an exact solution, but we're going to find an okay solution
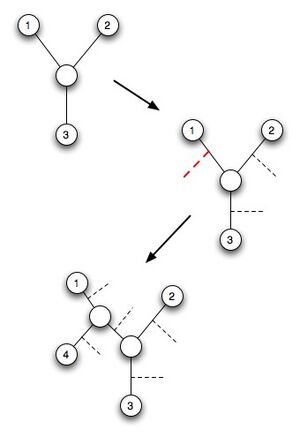
Calculate P(D|T)
- For some trees:
- compute L
- report best L
- build 3-leaf tree
- add a leaf
- try all possibilities
- keep the best one
- repeat until all leaves added
- change leaf order and repeat
Branch Lengths
- What are we going to do about branch lengths?
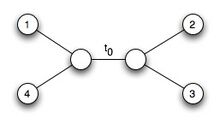
- There's no proof of this, but what we're going to do is look at one branch length at a time
- keeping all other branch lengths equal, let's find the length of t_o that maximizes the tree.
- Usually you get something that looks like:
- inverted parabola with big right shoulder (y-axis = L, x-axis = t_o)
- Branch lengths not very difficult to optimize.
- So it is a heuristic solution, but it is pretty good.