20.181/Lecture7

quick comment on upPass

• not necessary to find the best tree (you won't be tested on it)
• but here's the correct way to do it:

(from Peter Beerli's website)

definitions

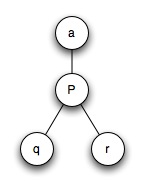
1. F_x: the upPass set we want to get to
   
2. S_x: the downpass set we got to
   
3. ancestor = a
   
4. parent = p, node we're looking at
   
5. children = q,r

Revisit overall strategy

• Although up until now we've always started with a tree of known topology, a lot of times you wouldn't know the tree topology beforehand

for all possible trees:

compute score (tree)

return best tree

Scoring functions

1. max parsimony (fewest mutations)
2. generalized parsimony (Sankoff: weighted mutation costs)
3. Maximum Likelihood

ML intro

• examples of a ML estimator:
  1. for normally distributed random var X, X(bar), the mean of the data you observe, is a ML estimator of the mean of the distribution they were drawn from
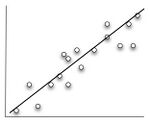
  2. A best fit line thru data is a ML estimator.

Probability Refresher

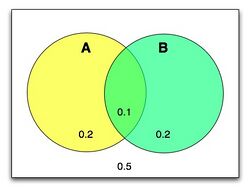
total area of a box = 1

p(A)= 0.3 , p(B)= 0.3
p(A,B)= 0.1
p(A|B)= 0.1 / (0.1+0.2) = 1/3 = p(A,B) / p(B)
p(B|A) = 0.1 / (0.1+0.2) = p(A,B) / p(A)
With a little manipulation we can derive Bayes' Rule:
p(A|B) = p(B|A) * p(A) / p(B)

ML in trees

• We are looking for the best tree, given some data. What is the best tree T given the data D?

p(T|D) is what we want to maximize

Not obvious how we want to do that... use Bayes Law to rearrange into something we can intuitively understand

p(T|D) = p(D|T) * p(T) / p(D)

• p(D) is a constant ... we don't have to worry about it
• What is p(T), the a priori probability of the tree ?

Well, without looking at the data, do we have a way of saying any tree is more likely than another one if they don't have any data associated with them ?

No... not really

• So what we're left maximizing is just p(D|T) and that sounds like a familiar concept!

NOTE: Tree now consists of topology AND distances We ask, what is the probability of each mutation occuring along a branch of a certain length? What is the probability that they ALL occurred, to give us the sequences we see today?

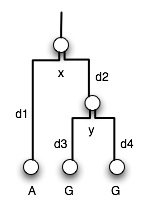
p(D|T) = p(x->A|d_1) * p(x->y|d_2) * p(y->G|d_3) * p(y->G|d_4)
p(A U B) = p(A) + p(B) - p(A,B)
p(A <intersect> B) = p(A)*p(B)

• We treat all of these mutations along the different branches as independent events (that's why you multiply the probabilities, because all the events have to happen independently.)

Jukes-Cantor

• based on a simple cost "matrix"
  

probability of changing from one particular nucleotide to another particular nucleotide is 'a'

probability of any nucleotide staying the same is '1-3a'

if x == y :

[JC eqn you'll derive in the hw]

if x != y :

[JC eqn you'll derive in the hw]

Evolutionary Model

gives us likelihood of (D|T) (need branch lengths)

downPass for ML

compute L(p|q,r,d)

q , r = likelihood of the two subtrees, d are the distances to them