20.181/Lecture5
From OpenWetWare
Jump to navigationJump to search
Downpass (cont.)
The tree we were working on last time:
Now we're going to try to code up the downpass.
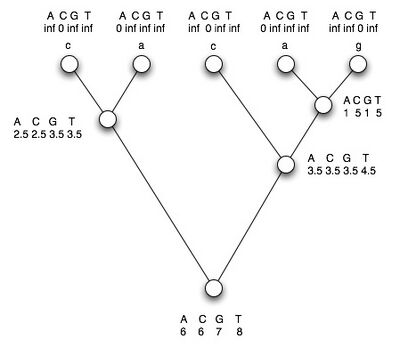
- So now we want to know: what is the sequence at this ancestor node, that we can't observe? We'll try all four possibilities, and calculate the penatly associated with each of those possibilities are.
- Remember that the good solution with the fibonacci series was to pass all the information back each time so that we don't have to repeat calculations!
- We left off at the root node, where we said there were 64 possibilities.
- So let's go through this by hand and try to write pseudo code for a function that will do the same thing.
- What we're going to do, which might seem odd at first, is to pass the node's identity (nodeSeq) (A,C,G,or T) into the function as if we know it. Our function will look at this one possibility and return one column of the cost vector. We will pass to this function each possibility, one by one.
Sankoff Downpass Algorithm
(See lecture 8 notes for a more efficient way of implementing Sankoff downpass)
def sankoff(tree,nodeSeq):
- min = inf #initialization
- if tree is a leaf: #stop condition
- if tree['data'] == nodeSeq:
- return 0
- return inf
- for leftSeq in [A,C,G,T]: #now we're at a node with two children
- for rightSeq in [A,C,G,T]: #we have to try all 16 possibilities here
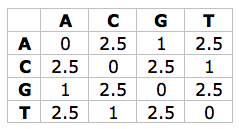
- sum= cost(nodeSeq,leftSeq,rightSeq) #cost is some function that looks up the cost in the table
- sum += sankoff(tree['left'],leftSeq) #we have to remember to pass the cost along!
- sum += sankoff(tree['right'],rightSeq)
- if (sum < min):
- min = sum
- return min
def sankoffDownpass(tree): #we don't know what the sequence is at the root
- for seq in [A,C,G,T]:
- if sankoff(tree,seq) < min:
- min = sankoff(tree,seq)
- minSeq = seq
- return min
Downpass: can we stop there?
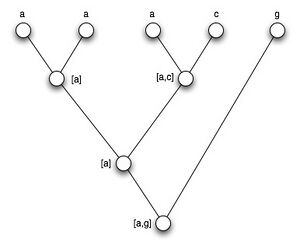
- So far we're only passing the best score obtained at each subtree down the tree to the root.
- The downPass algorithm, which you'll implement in HW4, finds the most parsimonious sequence at the root node.
- Why does it find the most parsimonious sequence only for the root ?
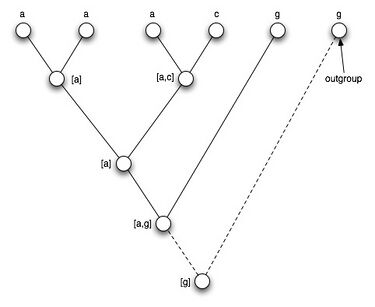
- Think about what the difference is between the root and the other internal nodes:
- the root doesn't have any parents -- only children.
- Think about what the difference is between the root and the other internal nodes:
- So far, all our information flows down tree, and we use it to make inference about older and older internal nodes. That's why the inference at the root the best possible guess we can make; it has all the information from everywhere on the tree. But the inferences we've written at the internal nodes are NOT YET correct- these internal nodes only have part of the information on the tree.
- What if we added an outgroup, such that what was the root before is now an internal node
- would this change our guess about nucleotides that are likely at the old root?
- yes! because we would have additional information that had not been taken into account in our prior best guess
Fitch's upPass
We'll pass the information back up from the root node to the other internal nodes in order to decide what their most likely sequences were!
- computer science jargon: three ways to traverse trees
- pre-order: do some operation, then call left subtree, then call right subtree
- like typing into a calculator: + 5 3
- in-order: L, op, R
- like typing into a calculator: 5 + 3
- post-order: L, R, op
- like typing into a calculator: 5 3 +
- pre-order: do some operation, then call left subtree, then call right subtree