20.109(S08):Data analysis (Day7)

Introduction

This is it, folks! Moment of truth. Time to find out how the proteins that you worked so hard to make, purify, and test really behave. Although you should be able to produce reasonable titration curves by following the example of Nagai, the introduction/review of binding constants below may help contextualize your analysis.

Simple Binding Curve The binding fraction y at first increases linearly as the starting ligand concentration is increased, then asymptotically approaches full saturation (y=1). The dissociation constant [math]\displaystyle{ K_D }[/math] is equal to the ligand concentration [L] for which y = 1/2.

Semilog Binding Curves By converting ligand concentrations to logspace, the dissociation constants are readily determined from the sigmoidal curves' inflection points. The three curves each represent different ligand species. The middle curve has a [math]\displaystyle{ K_D }[/math] close to 10 nM, while the right-hand curve has a higher [math]\displaystyle{ K_D }[/math] and therefore lower affinity between ligand and receptor (vice-versa for the left-hand curve).

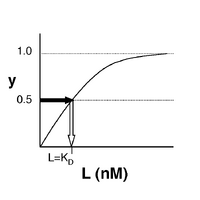
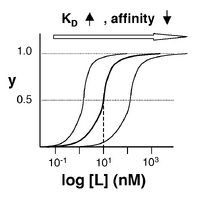
Let’s start by considering the simple case of a receptor-ligand pair that are exclusive to each other, and in which the receptor is monovalent. The ligand (L) and receptor (R) form a complex (C), which reaction can be written

[math]\displaystyle{ R + L \rightleftharpoons\ ^{k_f}_{k_r} C }[/math]

At equilibrium, the rates of the forward reaction (rate constant = [math]\displaystyle{ k_f }[/math]) and reverse reaction (rate constant = [math]\displaystyle{ k_r }[/math]) must be equivalent. Solving this equivalence yields an equilibrium dissociation constant [math]\displaystyle{ K_D }[/math], which may be defined either as [math]\displaystyle{ k_r/k_f }[/math], or as [math]\displaystyle{ [R][L]/[C] }[/math], where brackets indicate the molar concentration of a species. Meanwhile, the fraction of receptors that are bound to ligand at equilibrium, often called y, is [math]\displaystyle{ C/R_{TOT} }[/math], where [math]\displaystyle{ R_{TOT} }[/math] indicates total (both bound and unbound) receptors. Note that the position of the equilibrium (i.e., y) depends on the starting concentrations of the reactants; however, [math]\displaystyle{ K_D }[/math] is always the same value. The total number of receptors [math]\displaystyle{ R_{TOT} }[/math]= [C] (ligand-bound receptors) + [R] (unbound receptors). Thus,

[math]\displaystyle{ \qquad y = {[C] \over R_{TOT}} \qquad = \qquad {[C] \over [C] + [R]} \qquad = \qquad {[L] \over [L] + [K_D]} \qquad }[/math]

where the right-hand equation was derived by algebraic substitution. If the ligand concentration is in excess of that of the receptor, [L] may be approximated as a constant, L, for any given equilibrium. Let’s explore the implications of this result:

• What happens when L << [math]\displaystyle{ K_D }[/math]?

→Then y ~ [math]\displaystyle{ L/K_D }[/math], and the binding fraction increases in a first-order fashion, directly proportional to L.

• What happens when L >> [math]\displaystyle{ K_D }[/math]?

→In this case y ~1, so the binding fraction becomes approximately constant, and the receptors are saturated.

• What happens when L = [math]\displaystyle{ K_D }[/math]?

→Then y = 0.5, and the fraction of receptors that are bound to ligand is 50%. This is why you can read [math]\displaystyle{ K_D }[/math] directly off of the plots in Nagai’s paper (compare Figure 3 and Table 1). When y = 0.5, the concentration of free calcium (our [L]) is equal to [math]\displaystyle{ K_D }[/math]. This is a great rule of thumb to know.

The figures at right demonstrate how to read [math]\displaystyle{ K_D }[/math] from binding curves. You will find semilog plots (bottom) particularly useful today, but the linear plot (top) can be a helpful visualization as well. Keep in mind that every L value is associated with a particular equilbrium value of y, while the curve as a whole gives information on the global equilibrium constant [math]\displaystyle{ K_D }[/math].

Of course, inverse pericam has multiple binding sites, and thus IPC-calcium binding is actually more complicated than in the example above. The [math]\displaystyle{ K_D }[/math] reported by Nagai is called an ‘apparent [math]\displaystyle{ K_D }[/math]’ because it reflects the overall avidity of multiple calcium binding sites, not their individual affinities for calcium. Normally, calmodulin has a low affinity (N-terminus) and a high affinity (C-terminus) pair of calcium binding sites. However, the E104Q mutant, which is the version of CaM used in inverse pericam, displays low-affinity binding at both termini. Moreover, the Hill coefficient, which quantifies cooperativity of binding in the case of multiple sites, is reported to be 1.0 for inverse pericam. This indicates that inverse pericam behaves as if it were binding only a single calcium ion per molecule. Thus, wild-type IPC is well-described by a single apparent [math]\displaystyle{ K_D }[/math].

Protocols

Part 1: Titration curve in Excel and first estimate of K_D

Today you will analyze the fluorescence data that you got last time. Begin by analyzing the wild-type protein as a check on your work (your curve should resemble Nagai's Figure 3L), then move on to your mutant samples. If you are not familiar with manipulations in Excel, use the Help menu or ask the teaching faculty for assistance.

1. Open an Excel file for your data analysis. Begin by making a column of the free calcium concentrations present in your twelve test solutions. Assuming a 1:1 dilution of protein with calcium, the concentrations are: 0.1 nM, 1 nM, 10 nM, 50 nM, 100 nM, 180 nM, 250 nM, 500 nM, 1 μM, 10 μM, 100 μM, 1000 μM. Be sure to convert all concentrations to the same units.
2. Now open the text file containing your raw data as a tab-delimited file in Excel (you can download the file from today's "talk" page). Convert the row-wise data to column-wise data (using Paste Special → Transpose), and transfer each column to your analysis file. Add column headers to indicate which protein is which. Also include a column of your control samples that did not contain protein.
3. Begin by calculating the average of your blank samples, and bold this number for easy reference. It is the background fluorescence present in the calcium solutions and should be quite low. Subtract this background value from each of your raw data values. It may help to have a 3-column series called “RAW”, and another called “SUBTRACTED.”
4. To get a sense of your data, you can plot the subtracted data as is (choose to plot points connected by a smooth line) and have a quick look at it. Note the approximate inflection points of the curves: these indicate the approximate values of the apparent [math]\displaystyle{ K_D }[/math]'s.
   • If your two replicate values for a given protein are wildly different, you may want to plot each curve separately. On the other hand, if your replicates are similar (as we expect), you will want to average them prior to plotting – this will improve the signal:noise of your dataset. When you do this, be sure to add error bars to your final plot.
5. To get a slightly more precise value of [math]\displaystyle{ K_D }[/math], you should normalize your data to resemble Figure 3L in the Nagai paper. The maximum and minimum fluorescence values for a given protein should be defined as 100% and 0% fluorescence, respectively, and every other fluorescence value should be expressed as a percentage in between. Plot this normalized data versus calcium concentration.
6. Once you have analyzed the data you obtained from the fluorescence plate reader in this way, load your old Nanodrop data for the wild-type protein, and analyze it as above. How does the benchtop, single replicate assay compare to the plate reader data? (Comment on this in your notebook.)
7. In class today or on your own time, prepare representative fluorescence curves for your wild-type and mutant proteins. These will be included in the data analysis portion of your portfolio.

Part 2: Improved estimate of K_D using MATLAB modeling

1. Download these three files: Fit_Main, Fit_SingleKD, and Fit_KDn. Move them to the C:/MATLAB72/work folder on your PC.
2. Double-click on the MATLAB icon to start up this software.
3. The main window that opens is called the command window: here is where you run programs (or directly input commands) and view outputs. You can also see and access the command history, workspace, and current directory windows, but you likely won’t need to today.
4. In the command window, type more on; this command allows you to scroll through multi-page output (using the spacebar), such as help files.
5. In addition to the command area, MATLAB comes with an editor. Click File → Open and select the program Fit_Main. It has the .m extension and thus is executable by MATLAB. Read the introductory comments (the beginning of a comment is indicated by a % sign), and then input your fluorescence data.
6. Read through the program, and as you encounter unfamiliar terms, return to the workspace and type help functioname. Feel free to ask questions of the teaching faculty as well.
   • You might read about such built-in functions as logspace and nlinfit.
   • You will also want to open and read Fit_SingleKD – a user-defined function called by Fit_Main – in the MATLAB editor.
   • If you type help function you will learn the syntax for a function header.
   • Note that a dot preceeding an operator (such as A ./ B or A .* B) is a way of telling MATLAB to perform element-by-element rather than matrix algebra.
   • Also note that when a line of code is not followed by a semi-colon, the value(s) resulting from the operation will be displayed in the command window.
7. Once you more-or-less follow Part 1 of the program, type Fit_Main in the workspace, hit return to run the program, and address the following questions in your notebook:
   • Why must the fluorescence data be transformed (from S to Y) prior to use in the model?
   • What [math]\displaystyle{ K_D }[/math] values are output in the command window, and how do they compare to the values you estimated from your Excel plots?
   • Figure 1 should display your wild type and mutant data points and model curves. How do they look in comparison to the curves you plotted in Excel?
   • Figure 2 should display the residuals (difference between data and model) for your three proteins. If the absolute values are low, this indicates good agreement between the model and the data numerically. Whether or not this is the case, another thing to look for is whether the residuals are evenly and randomly distributed about the zero-line. If there is a pattern to the errors, likely there is a systematic difference between the data and the model, and thus the model does not reflect the actual binding process well. What are the residuals like for each of your modeled proteins?
8. Now move on to Part 2 of the Fit_Main program. Part 2 also fits the data to a model with a single, ‘apparent’ value of [math]\displaystyle{ K_D }[/math], but it allows for multiple binding sites and tests for cooperativity among them. The parameter used to measure cooperativity is called the Hill coefficient. A Hill coefficient of 1 indicates independent binding sites, while greater or lesser values reflect positive or negative cooperativity, respectively. Again, address the following in your notebook:
   • Visually, which model appears to fit your wild-type data better (Fig. 3 vs. Fig. 1)?
   • Do the respective residuals support your qualitative assessment (Fig. 4 vs. Fig. 2)?
   • Numerically, how do the values of [math]\displaystyle{ K_D }[/math] compare for the two models? How does the value of n compare to the implicitly assumed value in Part 1?
9. Finally, you can skim Part 3 of the Fit_Main program. Don’t worry too much about the coding details, but do read through the comments.
   • Look at Part 1 of Figure 5: are the binding curves asymptotic, sigmoidal, or other? What does this indicate? You can use the zoom button to get a closer look at part of the plot, or the axis command present in the code. (Currently the latter has a % sign in front of it, so don’t worry about it unless you have time and are interested.)
   • Now look in the command window. What values of [math]\displaystyle{ K_A }[/math] and Hill coefficient (n) do you get for your three proteins? How do the [math]\displaystyle{ K_A }[/math]’s from Part 3 compare to the [math]\displaystyle{ K_D }[/math]’s from Parts 1 and 2? Don’t be discouraged if your wild-type values do not exactly match Nagai’s work, or if there is variation between Parts 1, 2, and 3. (As an example, for Part 1 I got [math]\displaystyle{ K_D }[/math] = 0.11, for Part 2 [math]\displaystyle{ K_D }[/math] = 0.14 and n = 2.8, and for Part 3 [math]\displaystyle{ K_A }[/math] = 0.060, and n = 0.63 for a wild-type protein I tested.)
   • What is the relationship between slope and intercept, and [math]\displaystyle{ K_A }[/math] and n?
   • Comparing the model and data points by eye (Part 2 of Figure 5), do you think it is a good model for any of your proteins? If so, which ones? If your mutant proteins are not well-described by these models, what kind of model(s) (qualitatively speaking) do you think might be useful?

For next time

1. Update: Part 2 due date has been moved to one week from today. Parts 1-3 of your portfolio are due next time (Thursday or Friday, depending on your lab section) by 11 am. If you have been keeping up with the homework assignments, Parts 1 and 2 should be nearly done already. Please email all three parts according to the instructions.
2. Please also email your finished journal club presentation to astachow AT mit DOT edu. The order in which your presentations are received will be the order of speakers. Suitable articles for presenting are here but you should not feel restricted to this list. If you have another article in mind please email me the citation for approval. Finally, don't forget to re-read the 20.109(S08):Guidelines for oral presentations.