Physics307L:People/Muehlmeyer/Formal
SJK 03:25, 8 December 2008 (EST)

You have some very good work in here and this is a good first draft of the formal report. There are some very important things missing (e.g. the introduction and citations to original peer-reviewed research reports. Also, I am recommending some major reorganization of some material as described below (such as moving "data" to the "results and discussion section" which right now does not have any text). After having put all this thought into this report, you should be able to approach the experiment tomorrow with a goal of trying out your "best" method and seeing if you can get even more precise data. Or investigating any other interesting aspect of the experiment further.
Measuring the Speed of Light
Author: Justin Muehlmeyer
Experimentalists: Justin Muehlmeyer and Alexander Barron
University of New Mexico
Department of Physics and Astronomy Junior Lab November 2008
jmuehlme@unm.edu
SJK 02:55, 8 December 2008 (EST)

Good contact info. For a research publication, it would be good to have a more descriptive title, so the reader would have a better idea of what he'd find in the report.
Abstract
SJK 02:53, 8 December 2008 (EST)

This abstract is very informative and easy to read. You can strengthen it by adding a "motivation" or importance statement at the beginning or end or possibly a "future work" kind of statement. Since you're including your value in the abstract, you should include the uncertainty too.
To approximate the speed of light we measured the "flight time" of pulses of light emitted by a light emitting diode by measuring the time difference between LED emission and PMT reception of the light signal down a tube via a time amplitude convertor (TAC). By varying the distance the light signal travels we plot distance vs. flight time and use the linear-least squares method to approximate the slope of our data, which gives us the speed of light. We found that our best approximation to the accepted value of 2.99 X 108 m/s was 2.94 X 108 m/s, which came from large variations in distance and from using the "time walk" correction that accounts for the changing intensity of the light as the LED distance approaches the PMT.
Introduction
SJK 03:22, 8 December 2008 (EST)

this section is important, and as you probably know it's not easy to write. Make sure you leave yourself enough time to write it. This section is also where you will cite your original research references.
Materials and methods
SJK 03:20, 8 December 2008 (EST)

You have extensive methods, which I think is good because this experiment is actually quite complicated in terms of how to get rid of systematic error. So, I think most of your information is good and necessary. However, I have some major style points to make. (1) First, typically there is not a list of equipment, but rather the equipment is mentioned in the text of the methods. For example, "...pointing in at the PMT (model N-134, Perfection Mica Company, CITYNAME)...". (2) Your text is sometimes informal. I think this can be fixed by making sure that all of your text is past tense about pertinent things you actually did and is not "how to" statements of hypothetical occurrences. For example, the statement "Then we remembered that the oscilloscope can do the averaging for us." would not be used in a formal report, and that whole paragraph may be extraneous if you only use data from the "better" method.
Instrumentation
- PMT: Perfection Mica Company N-134
- Digital Oscilloscope: Tektronics TDS 1002
- LED: Cycles on and off at around 10KHz depending on the voltage applied. Recommended voltage is around 200 volts DC.
- LED Power Supply:
- PMT Power Supply:
- Cardboard tube wide enough to fit the PMT on one end and LED on the other.
- 2 Polarizing filters: one for the PMT, one for the LED.
Set Up
A long cardboard tube has the LED on one end pointing in at the PMT receiving its signals on the other end. The LED is strapped to 3 meter sticks binded by tape so that we can push the LED down the tube and measure the change in distance from its initial point. The PMT and LED each have a polarizer attached to their fronts, so that as we push the LED in we can rotate the PMT on the other end to maintain a constant intensity (see segment on intensity and time walk below). The anode of the PMT is connected to the input on the delay module and to channel 1 of the oscilloscope.
The LED is connected to its power supply via a BNC cable. We have the LED power supply outputing 190 V. The PMT is connected via a BNC to its high voltage source outputing at 1900 V.
To measure the time difference between LED emission and PMT reception we have a time amplitude converter (TAC) which converts the time difference of its inputs into a voltage that is proportional to that time difference. The two BNC inputs are labeled the "start" time from LED emission, and the "stop" time from PMT reception through the delay module. The output ratio of the time difference between the two inputs is 10 V = 50 nS, which we read on the digital oscilloscope in channel 2.
Time Walk
Since our TAC triggers at a fixed voltage, its triggering time occurs later for small incoming amplitudes then larger ones. This creates an issue because as we push the LED in closer to the PMT, the PMT signal increases in amplitude and the "time walk" problem then becomes a large source of systematic error. To avoid this issue we must maintain a constant PMT signal by using the polarizers to maintain constant intensity on the PMT.
The intensity was kept constant by rotating the PMT by slight amounts which rotated the polarizer covering its "lens". The polarizer "filters" or "cuts" the incoming light's electric field based on the angle that the polarizer film molecules are aligned. There is a point (or angle rather) when the polarizer cuts the incoming light entirely, and no voltage can be seen from he TAC at all. This means the alignment of the polarizer with the incoming electric field from the LED is perindicular. This is found to be of great importance, if we don't maintain a constant intensity for the PMT reception then our actual time difference will be skewed due to the fact that the TAC is receiving more signals from the PMT then it should.
Procedure
We varied the distance between the LED module and the photomultiplier tube, taking voltage measurements from the oscilloscope.
We used two methods to read the data on the oscilloscope. The raw signal from the TAC when the oscilloscope is in "sample" mode is very turbulent and quite impossible to read. We first used the cursors to eye an average, then with the second cursor we eyed the deviations from this average. This was time consuming, and somewhat frustrating due to the extreme variations of the signal. Then we remembered that the oscilloscope can do the averaging for us.
Setting the oscilloscope data acquisition mode to "average", the oscilloscope does all the work for us. Over a period of time it takes an average and displays it. Therefore the signal we see is actually delayed from the actual input but is a better representation. So we decided to take all of our data using the "measure" function on the oscilloscope when the data acqusition mode was on "average". This of course is an easier way of doing it, and we took all of our data later using the measure function for efficiency sake. The measure function does not read the deviation however, so this value had to be eyed based on the fluctations of the signal from that average.
Plotting the distance vs. time and taking the slope of the line best fit line of these points via the least-squares method produced an estimate for the speed of light. Please see our data below.
Data and Analysis
SJK 03:13, 8 December 2008 (EST)

Instead of having this "Data and Analysis" section, instead it looks like most of the "analysis" section should be moved to the methods section. And the "data" section would be moved to the "results and discussion" section. Information about the methods for each trial should be in the methods. Yeah I know a little confusing, but we can talk about it tomorrow.
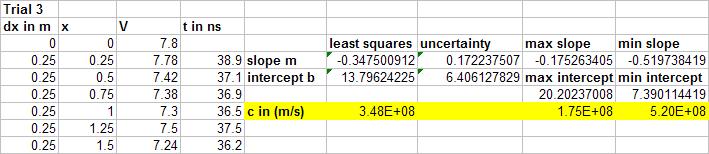
Data
We did four trials, each with different changes in distance, and the last to see the importance of the time walk correction:
Trial 1 distance changes increased rapidly from the initial point.
Trial 2 was to see what small changes in distances would give.
Trial 3 was for large changes in distance, but not as large as trial 1.
Trial 4 was to check the importance of time walk correction. We did not use the polarizers here to correct for the changing intensity.
Error
SJK 03:10, 8 December 2008 (EST)

Each of the above tables should have a caption. This information about the error could probably be put in the caption(s).
All voltages were measured to have an uncertainty of ± 0.02 V due to the oscilloscope reading. This is accounted for in our data plots where on our time axis we will see error bars of ± 0.1 nS. This comes from oour TAC ratio of 10 V = 50 nS.
Analysis
SJK 03:12, 8 December 2008 (EST)

Most of this section probably belongs in the Methods section, under an "analysis" heading (maybe that's what you intended already?). When mentioning Excel, you'd put the company name (Microsoft, Redmond, WA).
According to Taylor (see references) we determine the coefficients of a best fit linear line [math]\displaystyle{ y = A + Bx }[/math] by the relations below.
- [math]\displaystyle{ A=\frac{\sum x_i^2 \sum y_i - \sum x_i \sum x_i y_i}{\Delta_{fixed}} }[/math] [math]\displaystyle{ \mbox{,}~~~~~~~~~~~~~~~~~ \sigma_a^2 = \frac{\sigma_y^2}{\Delta_{fixed}} \sum x_i^2 }[/math]
- [math]\displaystyle{ B=\frac{N\sum x_i y_i - \sum x_i \sum y_i}{\Delta_{fixed}} }[/math] [math]\displaystyle{ \mbox{,}~~~~~~~~~~~~~~~~~ \sigma_b^2 = N \frac{\sigma_y^2}{\Delta_{fixed}} }[/math]
- [math]\displaystyle{ \Delta_{fixed}=N \sum x_i^2 - \left ( \sum x_i \right )^2 }[/math]
The LINEST function in EXCEL in fact outputs these coefficients for us, which I calculated above in my data tables. Outputs of the function are the slope of the best fit line, the y-intercepts of that slope, and the uncertainites in both the slope and the y-intercept.
The uncertainties in these values create an upper and lower bound for our values of the speed of light. The maximum slope is produced by adding the mean slope and the standard error of the slope. The minimum slope is the mean slope minus the standard error of the slope. The maximum and minimum y-intercepts, are the mean y-intercept plus and minus the standard error of the y-intercept, respectively.
By forcing the linear best fit line to the y-intercepts we can attain our maximum and minimum values for the speed of light when the least-squares method is implemented.
See results below.
My data analysis Excel workesheet can be accessed here:
File:Speed of Light Data Analysis Formal.xls
Results and Discussion
SJK 03:05, 8 December 2008 (EST)

This is an interesting way of presenting the data, a combo table / figures. It's not typically done in research papers, at least as far as I can think now...but I do like it and think it's an effective way of concisely presenting your results. I like your figures with the dotted lines for showing the range of uncertainty. Make sure to number this "figure" and to give it an overall caption and / or individual descriptive captions -- so the reader would be able to understand the data / figures without having to read elsewhere in the text.
You will probably notice that your "results and discussion" section is blank besides this table. I am commenting out of order, so I suspect that a lot of your material from above this section actually will be moved to this seciton.
| Trial | Graphic Representation | Trial | Graphic Representation |
|
Trial 1: rapid and largest distance changes
Upper Error Bound:
Lower Error Bound:
|
|
Trial 2: small and constant distance changes
Upper Error Bound:
Lower Error Bound:
|
|
|
Trial 3: larger and constant distance changes
Upper Error Bound:
Lower Error Bound:
|
|
Trial 4: no time walk correction
Upper Error Bound:
Lower Error Bound:
|
|
Conclusion
SJK 03:08, 8 December 2008 (EST)

You should include the uncertainty estimate with this final value...this of course is how you know whether your answer is "consistent" with the accepted value. Also, part of your conclusion should be some kind of "importance" or impact statement and / or some statement of work that could be carried out next after the work in this report.
The results show the importance of large changes in distance of the LED, and the necessity of the time walk correction.
Our best approximation to the true value was trial 1 with a value of [math]\displaystyle{ {c}=2.91\cdot 10^{8}\frac{m}{s} }[/math].
This trial was characterized by changes of distance that were increasingly large, showing the importance of large changes of distance. Also of importance was the time walk correction.
Our approximation has a percent error from the actual of only 2.7 %, showing that our method was systematically accurate.
Acknowledgements
SJK 03:08, 8 December 2008 (EST)

This section is good.
Thanks to my lab partner Alexander "Der" Barron, our lab professor Dr. Steven Koch, and our lab TA, Aram Gragossian.
References
SJK 03:09, 8 December 2008 (EST)

These are both good things to cite, but neither is an original peer-reviewed research publication. Your introduction section is missing, and that is where you will most likely put the original research citations.
Gold, Michael. 2006. PHYSICS 307L: Junior Laboratory. The University of New Mexico, Dept. of Physics and Astronomy. Online at <http://www-hep.phys.unm.edu/~gold/phys307L/manual.pdf>.
Taylor, John R. 1997. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books, 2 ed.