IGEM:IMPERIAL/2008/Modelling/Tutorial2
<html> <style type="text/css"> .firstHeading {display: none;} </style> </html> <html> <style type="text/css">
table.calendar { margin:0; padding:2px; }
table.calendar td { margin:0; padding:1px; vertical-align:top; } table.month .heading td { padding:1px; background-color:#FFFFFF; text-align:center; font-size:120%; font-weight:bold; } table.month .dow td { text-align:center; font-size:110%; } table.month td.today { background-color:#3366FF } table.month td {
border:2px; margin:0; padding:0pt 1.5pt; font-size:8pt; text-align:right; background-color:#FFFFFF; }
- bodyContent table.month a { background:none; padding:0 }
.day-active { font-weight:bold; } .day-empty { color:black; } </style> </html>
| <html><a href=http://openwetware.org/wiki/IGEM:IMPERIAL/2008/Prototype><img width=50px src=http://openwetware.org/images/f/f2/Imperial_2008_Logo.png></img</a></html> | Home | The Project | B.subtilis Chassis | Wet Lab | Dry Lab | Notebook |
|---|
<html> <style type="text/css"> div.Section { font:11pt/16pt Calibri, Verdana, Arial, Geneva, sans-serif; }
/* Text (paragraphs) */ div.Section p { font:11pt/16pt Calibri, Verdana, Arial, Geneva, sans-serif; text-align:justify; margin-top:0px; margin-left:30px; margin-right:30px; }
/* Headings */ div.Section h1 { font:22pt Calibri, Verdana, Arial, Geneva, sans-serif; text-align:left; color:#3366FF; }
/* Subheadings */ div.Section h2 { font:18pt Calibri, Verdana, Arial, Geneva, sans-serif; color:#3366FF; margin-left:5px; }
/* Subsubheadings */ div.Section h3 { font:16pt Calibri, Verdana, Arial, sans-serif; font-weight:bold; color:#3366FF; margin-left:10px; }
/* Subsubsubheadings */ div.Section h4 { font:12pt Calibri, Verdana, Arial, sans-serif; color:#3366FF; margin-left:15px; }
/* Subsubsubsubheadings */ div.Section h5 { font:12pt Calibri, Verdana, Arial, sans-serif; color:#3366FF; margin-left:20px; }
/* References */ div.Section h6 { font:12pt Calibri, Verdana, Arial, sans-serif; font-weight:bold; font-style:italic; color:#3366FF; margin-left:25px; }
/* Hyperlinks */ div.Section a {
}
div.Section a:hover {
}
/* Tables */ div.Section td { font:11pt/16pt Calibri, Verdana, Arial, Geneva, sans-serif; text-align:justify; vertical-align:top; padding:2px 4px 2px 4px; }
/* Lists */ div.Section li { font:11pt/16pt Calibri, Verdana, Arial, Geneva, sans-serif; text-align:left; margin-top:0px; margin-left:30px; margin-right:0px; }
/* TOC stuff */ table.toc { margin-left:10px; }
table.toc li { font: 11pt/16pt Calibri, Verdana, Arial, Geneva, sans-serif; text-align: justify; margin-top: 0px; margin-left:2px; margin-right:2px; }
/* [edit] links */ span.editsection { color:#BBBBBB; font-size:10pt; font-weight:normal; font-style:normal; vertical-align:bottom; } span.editsection a { color:#BBBBBB; font-size:10pt; font-weight:normal; font-style:normal; vertical-align:bottom; } span.editsection a:hover { color:#3366FF; font-size:10pt; font-weight:normal; font-style:normal; vertical-align:bottom; }
- sddm {
margin: 0; padding: 0; z-index: 30 }
- sddm li {
margin: 0; padding: 0; list-style: none; float: center; font: bold 12pt Calibri, Verdana, Arial, Geneva, sans-serif; border: 0px }
- sddm li a {
display: block; margin: 0px 0px 0px 0px; padding: 0 0 12px 0; background: #33bbff; color: #FFFFFF; text-align: center; text-decoration: none; }
- sddm li a:hover {
border: 0px }
- sddm div {
position: absolute; visibility: hidden; margin: 0; padding: 0; background: #33bbff; border: 1px solid #33bbff } #sddm div a { position: relative; display: block; margin: 0; padding: 5px 10px; width: auto; white-space: nowrap; text-align: left; text-decoration: none; background: #FFFFFF; color: #2875DE; font: 11pt Calibri, Verdana, Arial, Geneva, sans-serif } #sddm div a:hover { background: #33bbff; color: #FFFFFF } </style></html>
Pre-Analysis Data Processing
The outcome of the motility assay is a movie, in the form of a sequence of frames. A bacteria-tracking algorithm can be applied to these frames. For the moment we will not question the output to the tracking algorithm. The times and positions it yields are therefore considered exact.
In reality, limitations on the tracking of motile B. subtilis include
- Determining the centre of the organism as it moves in order to define a co-ordinate for the position,
- Frame-rate of video capture - can we capture all the relevant movements the organism makes?
- Resolution of the images - are the images high enough resolution to allow us to accurately resolve the location of the organism?
- Errors in the algorithm analysing the images
In order to analyse the data, they must be broken into manageable subsets
- Design a routine to convert the trajectory of a bacterium into the relevant times, angle, velocities etc…
- Apply your routine to your synthetic dataset(s)
- Crude Error Checking: Plot the relevant histograms and compare them to histograms of the synthetic dataset(s) generated in Tutorial 1 (they should be the same)
With the kind of motion mentioned in Tutorial 1, the trajectory can be split into four sets of independent data (time, velocity, angle, turning time). However, we can expect velocity and time to be linked.
How can we expect velocity and time to be linked if we are assuming normal distribution of a uniform velocity? Are we assuming that the more towards the centre of the normal distribution the run-time is, the more towards the centre of the normal distribution the velocity will be?
The turning time is not really recorded in the output from our model.
- In the likely event they are indeed linked, modify the pre-analysis data processing – and the error checking – accordingly.
Parameter Estimation
In mathematical modelling, hypotheses about the process of interest (in this case, the motility of B. subtilis) are stated as parametric families of probability distributions, called models (see Tutorial 1).
The goal of modelling is to make discoveries about the underlying process, by testing these hypotheses.
Once a model, together with its parameters, has been specified, and data has been gathered, the model can be evlaluated.
The parameters of a statistical distribution can be estimated from a set of samples in many different ways. The most common way is to apply an estimator to the distribution, in order to extract its parameters.
Maximum Likelihood
The concept of likelihood is related to the more familiar concept of probability. The best explanation that I found online is here.
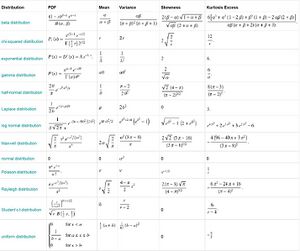
Maximum likelihood estimators of some standard distributions are given below.
| Distribution | MLE |
| Gaussian Distribution | [math]\displaystyle{ \widehat{\theta} = \left(\widehat{\mu},\widehat{\sigma}^2\right), }[/math] where [math]\displaystyle{ E \left[ \widehat\mu \right] = \mu, }[/math] and [math]\displaystyle{ E \left[ \widehat{\sigma^2} \right]= \frac{n-1}{n}\sigma^2 }[/math]. |
| Exponential Distribution | [math]\displaystyle{ \widehat{\lambda} = \frac1{\overline{x}}. }[/math] |
| Poisson Distribution | [math]\displaystyle{ \widehat{\lambda}_\mathrm{MLE}=\frac{1}{n}\sum_{i=1}^n k_i. \! }[/math] |
| Uniform Distribution | [math]\displaystyle{ \widehat{A}=a-h, \widehat{B}=a+h }[/math] |
| Von Mises Distribution | |
| Ricean Distribution | [math]\displaystyle{ \widehat{A}_c = \sqrt{\langle M^2 \rangle - 2 \sigma^2} }[/math], which is a conventional estimator. This paper discusses the derivation of MLE for a Rice Distribution [1] |
| Maxwellian Distribution |
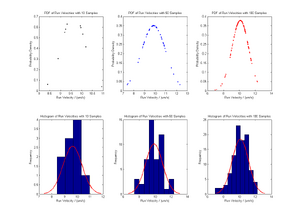
The experimental data we obtain does not give us access to the entire underlying distribution. We hope that the data are representative of the underlying distribution. The amount of data we use to estimate the parameters is therefore a crucial factor in the accuracy of the outcome. By applying the relevant estimator to the synthetic dataset we generated, we can see that increasing the size of the data set increases the accuracy with which we can estimate the parameter. The order of the data set does not influence the likelihood. Advantages and disadvantages of the MLE approach to parameter estimation are summarized here
Moments
Another possible method is to recombine the moments of the distribution in such a way that the outcome is a parameter of the distribution.
- What is the definition of mn (the nth moment of a distribution)?
The nth moment of a distribution is defined by: [math]\displaystyle{ \mu_n^'=\langle x^n \rangle }[/math]. Take a look at this site for detailed explanations.
- Often we prefer centred moment for n>1. What is their definition?
Centred moment at n=1 is defined as the mean of the distribution. By taking moments with respect to the mean, we can obtain the shape of the graph with respect to the average of the distribution. This is convenient for common distributions such as the Gaussian and Maxwell-Boltzmann distributions, among many others. Take a look at this site for more details on central moments.
- How do we call the centred moments of second, third and fourth order?
Centred moments of 2nd order is the Variance, 3rd order refers to the Skewness and 4th order refers to the Kurtosis of the distribution.
- What do they measure?
- Variance is given by: [math]\displaystyle{ \sigma^2=\int P(x)(x-\mu)^2 dx }[/math]. It gives a measure of statistical dispersion (degree of being spread out), averaging the squared distance of its possible values from the mean.
- Skewness is the third standardized moment and is defined as: [math]\displaystyle{ \gamma_1 = \frac{\mu_3}{\sigma^3} }[/math]. It is a measure of the degree of asymmetry of a distribution. If the left tail is more pronounced (elongated) than the right tail, the function is said to have negative skewness. If the reverse is true, it has positive skewness. If the two are equal, it has zero skewness. This site gives a table of skewness for common distributions.
- Kurtosis is the degree of peakedness of a distribution and is defined as: [math]\displaystyle{ \frac{\mu_4}{\sigma^4}\ }[/math]. A high kurtosis distribution has a sharper "peak" and fatter "tails", while a low kurtosis distribution has a more rounded peak with wider "shoulders". This site provides good examples of various distributions with positive and negative kurtosis.
This site gives an outline on how to derive moments using the Moment-Generating Function.
Recombining the moments [math]\displaystyle{ m_1 \dots m_n }[/math] in order to estimate the parameters [math]\displaystyle{ \alpha_1\dots\alpha_p }[/math] consists of identifying the functions [math]\displaystyle{ g_1 \dots g_p }[/math] such that
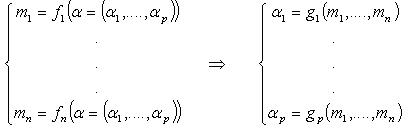
- Apply the method to the Gaussian, Exponential, Poisson distributions…
- The functions g1… gp are not unique - see the case of the exponential distribution. How do you think the discrepancies between the various formulae can be exploited?
Again we never have access to the entire distributions, only to data that we think are representative of the distribution. The amount of data we use to estimate the parameters is again crucial for the accuracy of the outcome.
- Calculate the first four moments with various amounts of data
- For instance use 10 samples, 50 samples, 100 samples
- Does the order of your data have a significant influence?
- Apply the recombination to the computed sample-moments of distributions of your choice
- Compare the accuracy of the approach to the results obtained with ML.
- Discuss the pros and cons of the method
Bayes Theorem
Bayes theorem states that [math]\displaystyle{ P(A|B)=\frac{P(B|A)P(A)}{P(B)} }[/math] where [math]\displaystyle{ P(A|B) }[/math] is termed the posterior probability, and the terms on the right hand side are the prior probabilities.
- What is Bayes’ update rule? What is its meaning?
References
<biblio>#Rice Maximum likelihood estimation of Rician distribution parameters (1998) Jan Sijbers, Arnold J. Den Dekker, Paul Scheunders, Dirk Van Dyck. IEEE Transactions on Medical Imaging[1]
<html>
|
|
|