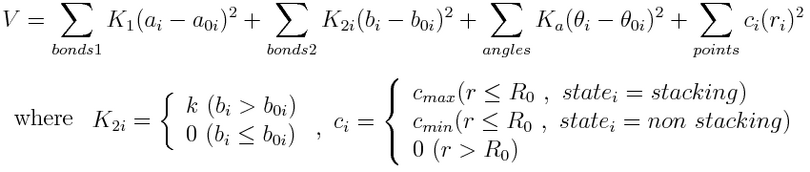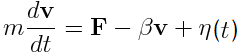Biomod/2011/TeamJapan/Sendai/Computational design/Simulation
<html>
<style rel="stylesheet" type="text/css">
.clear {clear:both;}
#verticalmenu {
/*this .CSS is inspired by http://www.javascriptkit.com/ */ font-family: "Comic Sans MS" , "Brush Script MT",serif, sans-serif, monospace, cursive, fantasy; list-style:none;}
- verticalmenu a:hover {
color: #aa1d1d; /* color when the click is over the main menu text-transform: uppercase; font-size: 10px; */
}
a:visited { color:#00a5ea; text-decoration: none }
.glossymenu, .glossymenu li ul{ list-style-type: none; margin: 0; padding: 0; width: 250px; /*WIDTH OF MAIN MENU ITEMS*/ border: 1px solid black; list-style:none; }
.glossymenu li{ position: relative; }
.glossymenu li a{ background: white url(http://openwetware.org/images/a/a7/Glossyback2.jpg) repeat-x bottom left; font: bold 17px Verdana, Helvetica, sans-serif; color: white; display: block; width: auto; padding: 10px 0; padding-left: 10px; text-decoration: none; }
.glossymenu li ul{ /*SUB MENU STYLE*/ position: absolute; width: 200px; /*WIDTH OF SUB MENU ITEMS*/
left: 0; top: 0; display: none; }
.glossymenu li ul li{ float: left; }
.glossymenu li ul a{ width: 190px; /*WIDTH OF SUB MENU ITEMS - 10px padding-left for A elements */ }
.glossymenu .arrowdiv{ position: absolute; right: 2px; background: transparent url(http://openwetware.org/images/6/69/Arrow.gif) no-repeat center right; }
.glossymenu li a:visited, .glossymenu li a:active{ color: white; }
.glossymenu li a:hover{ background-image: url(http://openwetware.org/images/5/50/Glossyback.jpg); }
/* Holly Hack for IE \*/
- html .glossymenu li { float: left; height: 1%; }
- html .glossymenu li a { height: 1%; }
/* End */
</style>
<script type="text/javascript">
/***********************************************
- CSS Vertical List Menu- by JavaScript Kit (www.javascriptkit.com)
- Menu interface credits: http://www.dynamicdrive.com/style/csslibrary/item/glossy-vertical-menu/
- This notice must stay intact for usage
- Visit JavaScript Kit at http://www.javascriptkit.com/ for this script and 100s more
- /
var menuids=new Array("verticalmenu") //Enter id(s) of UL menus, separated by commas var submenuoffset=-2 //Offset of submenus from main menu. Default is -2 pixels.
function createcssmenu(){ for (var i=0; i<menuids.length; i++){
var ultags=document.getElementById(menuids[i]).getElementsByTagName("ul")
for (var t=0; t<ultags.length; t++){
var spanref=document.createElement("span")
spanref.className="arrowdiv" spanref.innerHTML=" " ultags[t].parentNode.getElementsByTagName("a")[0].appendChild(spanref)
ultags[t].parentNode.onmouseover=function(){
this.getElementsByTagName("ul")[0].style.left=this.parentNode.offsetWidth+submenuoffset+"px"
this.getElementsByTagName("ul")[0].style.display="block"
}
ultags[t].parentNode.onmouseout=function(){
this.getElementsByTagName("ul")[0].style.display="none"
}
}
}
} if (window.addEventListener) window.addEventListener("load", createcssmenu, false) else if (window.attachEvent) window.attachEvent("onload", createcssmenu) </script>
|
<img src="http://openwetware.org/images/9/93/Simulationh.png" width="650">
|
</html> <html> <head> <style type="text/css">
- content {padding-left: 10px;width: 970px;}}
h3 {font-decoration: none;} h1.firstHeading {display: none; } </style> </head> </html>
<html> <style rel="stylesheet" type="text/css"> /*このスタイルシートの著作権はテンプレート工房TAKEにあります*/ /*ページのレイアウト用css*/
body{ background:#F5F5DC; /*壁色と壁紙設定*/ background-repeat:repeat;/*繰り返さない場合はno-repeatに変更*/ font:"メイリオ", "MS Pゴシック", Osaka, "ヒラギノ角ゴ Pro W3"; color: #333333; margin:0px; padding:0px; }
- contents{
width:900px;
margin:0 auto; background-color: #FFFFFF ;/*コンテンツ内の背景(サイズをぴったりにすること)*/ background-repeat:repeat-y; /*縦に繰り返し*/ border:solid 1px #666666;/*サイトに枠を付ける設定,色の変更可*/
position:relative;
font-size:80%;
}
/*ヘッダー部分の設定*/
- header{
background-image:url(http://openwetware.org/images/c/c4/TeamSendai-logo3.png) ;/*ヘーダー*/ background-repeat:repeat-x; /*縦に繰り返し*/ background-position:top right; height:140px; /*ヘーダーの高さ*/ }
- header p {
font-size: 26px;
color:#333333;
padding-top: 15px; padding-left: 20px; }
/*上部メニューボタンの設定*/
- navbar{
background-color:#FFFFFF;
width: 100%;
height:40px;
position:margine;
top:100px;
left:0px;
border-top:solid 1px #FFFFFF;
border-bottom:solid 1px #FFFFFF;
}
- navbar ul{
margin:0;
padding:0; list-style-type:none; font-family:Arial, Helvetica, sans-serif; font-size: 12px; line-height:40px; letter-spacing:2px; }
- navbar li{
background-color:#000099; /*上部メニューのボタンの背景*/
float:left; width:146px; /*メニューボタンの幅*/ text-align:center; padding:0; border-right:solid 1px #ffffff; }
- navbar ul a:hover{
background-color:#0033cc; /*メニューボタンにカーソルが来た時に背景*/
width:146px; /*メニューボタンの幅*/ }
- navbar a{
color:#ffffFF;/*メニューボタンの文字の色*/
display:block; }
- navbar a:hover{
color:#999999; /*メニューの文字がカーソルが来た時、この色に変わる*/ }
/*サイドメニューの設定*/
- side{
background-color:#ddffff;
width:220px;/*サイドの幅(変更するときはコンテンツ背景も変更すること)*/
position:margin; top:600px;/*上からの位置*/ left:12px; }
- side h3 {
font-size: 90%; border: double 3px #FFFFFF; color:#ffffff; text-align: center; background-color:#999999;
width:190px;
line-height: 30px; margin-top: 10px; margin-left: 5px; margin-bottom: 5px; }
- side h3 a {
color:#ffffff;
font-weight:normal; }
- side ul{
font-size:100%;
line-height:220%; /*サイドの文字と文字の行間設定*/ background-color: #ddffff; margin:0px; padding-left:10px; }
- side ul a:hover {
width:180px;
background-color: #99ffff; /*サイドのカーソルオーバー時の背景色*/ color: #999999; /*サイドのカーソルオーバー時の文字色*/ }
- side ul{
list-style-type:none;
padding-left:2px; }
- side li{
padding-left:15px; /*文字の左端からの位置*/ }
- side li a{
color:#333333;/*サイドの文字色*/
width:180px;
display:block;
}
- side .ad_list li{
background-image:none;
padding-left:0; }
/*右側メイン部分の設定*/
- main{
width:630px;
padding-top:15px;
margin-left:240px;
}
/*下部のフッター部分の設定*/
address{
font-size:80%;
font-style:normal;
text-align:center;
padding-top:5px;
}
address{
background-color:#000066;
color:#ffffff;
width:882px;
padding-bottom:10px; border:none; } address a{
color:#ff9999;
}
/*文字の設定*/ h1{ font-size:60%; letter-spacing: 2px; padding-left:10px; margin: 0px; }
h1 a{
color:#FFFFFF;
font-weight:normal; }
h2{
font-size:140%;
border-left: 10px solid #000066;
border-bottom:solid 1px #000099;/*文字の下に線を入れる設定*/
width:900px;
padding-left: 5px; color:#333333; margin-top: 15px; margin-bottom: 5px; }
h3{
font-size:120%;
border: solid 1px #111111;
color:#ffffff;
background-color:#4682B4 ; line-height: 30px; padding-left:10px; margin-top: 10px; margin-bottom: 1px; }
p{
font-size:90%;/*全体の文字サイズ*/
line-height:150%;/*全体で使う、文字と文字の行間*/
margin-left:5px;
}
p img{
float:left;
margin-top:5px; /*写真の左にスペースを空ける*/
margin-left:5px; /*写真の左にスペースを空ける*/
margin-right:10px; /:写真と文字の間隔*/ }
/*リンク文字の設定*/
a{
color:#000099;
text-decoration:none;
} a:hover { color: #FF0000;/*リンクの文字の上にマウスが来た時この色に変わる*/ text-decoration: none; }
- purple{
font-size:120%;
border: solid 1px #111111;
color:#ffffff;
background-color:#9370DB; line-height: 40px; padding-left:10px; margin-top: 10px; margin-bottom: 1px; }
h5{
font-size:120%;
border: solid 1px #111111;
color:#ffffff;
background-color:#FFA500; line-height: 30px; padding-left:10px; margin-top: 10px; margin-bottom: 1px; }
h6{
font-size:120%;
border: solid 1px #111111;
color:#ffffff;
background-color:#006400; line-height: 30px; padding-left:10px; margin-top: 10px; margin-bottom: 1px; }
- red{
font-size:120%;
border: solid 1px #111111;
color:#ffffff;
background-color:#DC143C; line-height: 40px; padding-left:10px; margin-top: 10px; margin-bottom: 1px; }
- blue{
font-size:120%;
border: solid 1px #111111;
color:#ffffff;
background-color:#191970; line-height: 40px; padding-left:10px; margin-top: 10px; margin-bottom: 1px; }
</style> </html>
<html>
3D simulation movie |
</html>
|
Provided ID could not be validated. |
Outline
<html>
<img src="http://openwetware.org/images/b/b7/Simulation_abstract.png" width="800"> |
</html>
About simulation
We did 3D simulation of the molecular rolling robot over the DNA origami field using molecular dynamics. In this simulation, the robot is represented as mass points and moves by following the Langevin equation. Hybridizing between robot legs and substrates on the field, and cleaving the substrates by legs, are described by a potential shift.
The program code was written entirely in C and OpenGL.
Model and Methods
In this simulation, we described the system as a coarse-grained model(1). In a coarse-grained model, representative points of the structures are extracted. In our case, these representative points were connected by springs and strings, and their potentials associated with them.
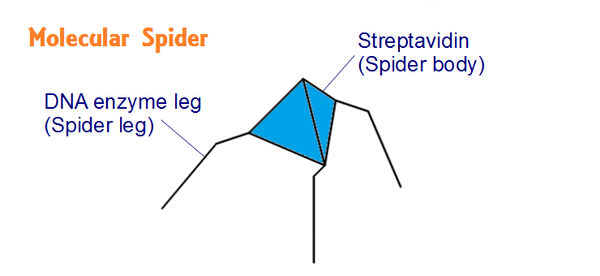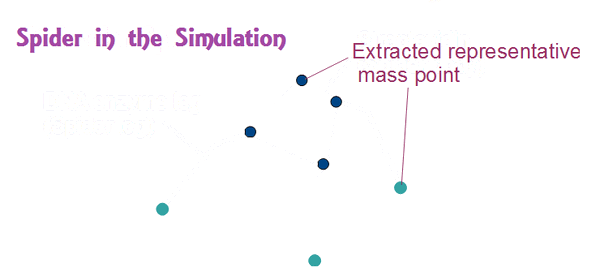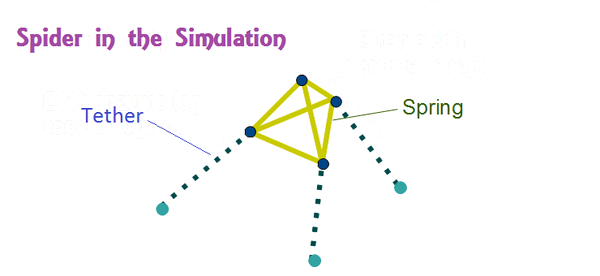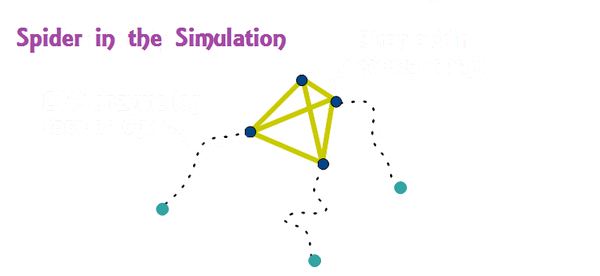
For example, see Fig.1, which represents extraction of corresponding points from the molecular spider, and a scheme of potential to maintain structure. Streptavidine structures were maintained by a spring-type potential which keeps length among points and weakly affect angles among points. Deoxyrybozyme legs were connected with a string-type potential, which is taken into consideration when points go beyond the determined length. On the spider simulation, blue points, green points, and yellow lines, represent mass points of the structure, top of spider legs, lines represents bonds, respectively.
Each mass point is moving under influence of energy V. The energy V is sum of potential energy for maintaining structure, and that for binding substrates on field. The potential of substrates is zero when legs are out of the effective area (as cut-off), and changes by distance between legs and substrates when legs enter effective area. The force from differentiation of the substrate potential is proportional to the distance.
<html></html>The motion of each mass point is described by the Langevin Equation(2). In this equation, acceleration is determined by sum of force F from the differentiation of energy V, viscosity resistance -βv , and white Gaussian random force η(t). White Gaussian random force was obtained by the box-muller methods(3). Distribution of the obtained random force is shown in Fig.2.
Langevin Equation
<html></html> <html></html>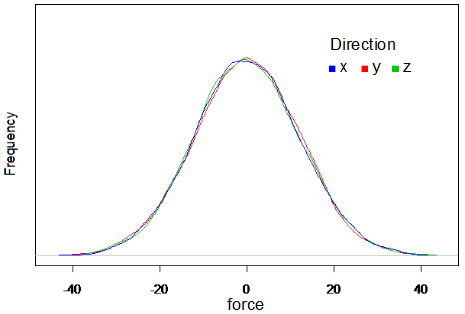
Spider simulation
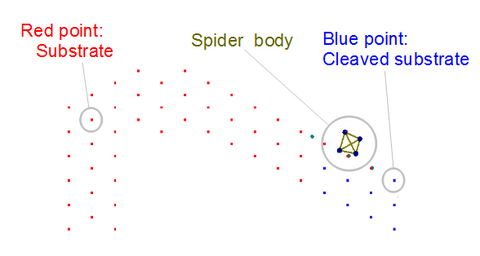
|
In order to deduce parameters, we simulated movements of DNA spider robot in the DNA spider article (Lund et al. 2010)(4). Red points and blue points represent uncleaved substrates and cleaved substrates, respectively. See the above movie, in which spider goes toward goal with cleaving substrates. |
Simulation data
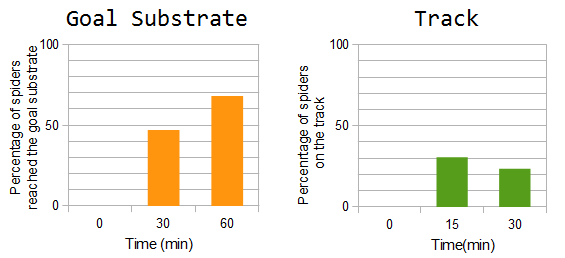
Fig.4 describes how many spiders reached the goal and how many did not at a certain time. We tuned simulation parameters to be consistence with the result in figure 2G of Lund et al. (Nature, 2010)(4). In our simulation, the time for reaching the goal substrate was about 20 times longer than the time that DNAzyme cleaved substrate. The result matched very well to the time in the article (about 21 times longer).
<html></html>Simulation of the triangular prism robot
|
Provided ID could not be validated. <html></html> |
We simulated whether our triangular prism robot can reach the goal of the field. The video in the left shows that our robot has high probability to reach the goal. We supposed that the triangular prism robot could reach the goal by only rotary motion. However, our simulation result indicated that the triangular prism moves forward by combination of, both, rotary motion and walking motion. This combined motion did not impede the robot efficiency for moving forward. Anyway, this design is satisfying our initial racing condition of reaching the goal.
|
Comparison between the spider and triangular prism robot
Provided ID could not be validated.
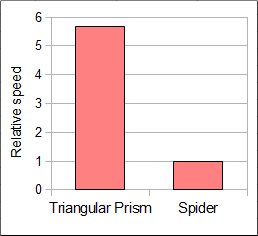
In order to examine which of the robots (our triangular prism or DNA spider) is the fastest in reaching the goal, a simulation was carried out. Locations of the substrates for the molecular spider were determined by following the design of the substrates in the original DNA spider paper, those positions are seen in the video. Locations of the substrate for our triangular prism robot were considered to be the same as our field design. Since the body of the triangular prism robot is bigger than the spider body, we could reduce the number of substrates for the prism on the field. It can be seen from this video that the triangular prism robot reaches the goal faster than the DNA spider.
Data of triangular prism simulation
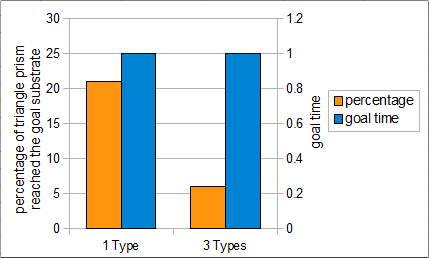
To check the effect of the number of leg-types over the time to reach the goal, speeds of triangular prism with 3 types of legs and with 1 type of legs were calculated by our simulation. The right part of Fig.6 shows the results. The goal time of both cases are very similar, but the percentage of the triangle prism was different. 1 leg type robot has a higher goal probability. Thus, we concluded that the 1 leg type robot could be better.
Other data
Cleavage rate and spider speed
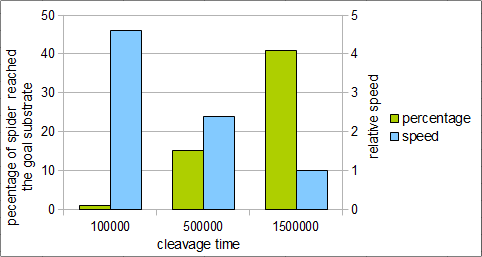
To verify effects of cleavage rates of DNAzyme, simulation of the molecular spider was done by changing cleavage time. Fig.7 is the result from our simulation. Increase of cleaving rate facilitated speed in reaching the goal, but percentage of spiders which reached goal reduced. Therefore, there is a trade-off between increasing the cleaving rate and the percentage of robots that reaches the goal.
Field design and spider speed
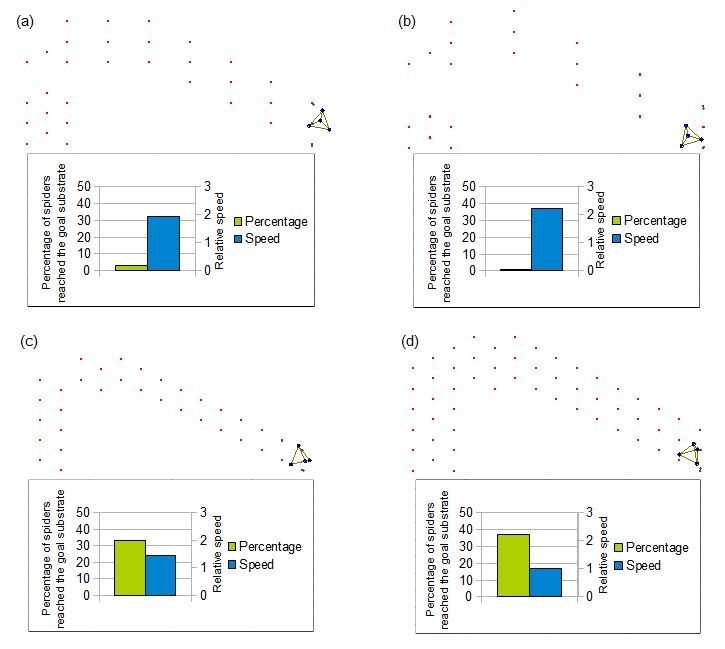
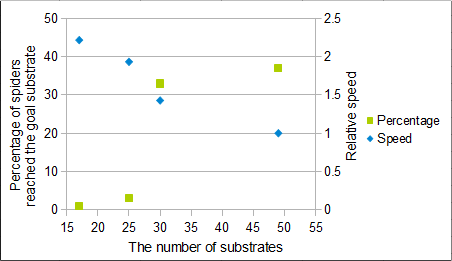
Fig.8 shows design of fields and moving data of spider over each field. Designs of these fields were based on the field used in the molecular spider article (figure 1d in Lund et al. Nature 2010))(4). Substrates in the field (a), (b), (c) are removed in a different pattern.
The results by the simulation are shown in the right figure. Less substrates gained speed to reach goal, and decreased probability of goal. But the goal probability depends on not only the number of substrates but also on the location of the substrates.
These suggested that it is better to reduce substrates on the field as much as possible to gain robot's speed.
<html></html>Body size and leg size
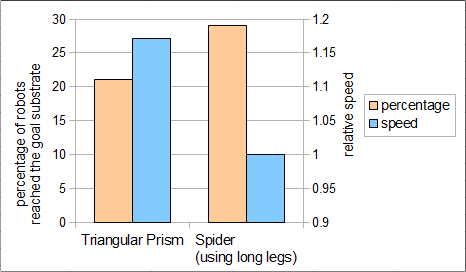
In this section, both robots, triangular prism and a modified molecular spider, were chased in silico on the same field. On this simulation, spider robot has longer legs, while design of triangular prism was the same as the one we used above. Right figure shows moving data of each robot. As a result, the molecular spider with long legs was slower than our robots, although it had more goal probability. It might be due to difference in the body size, leg length and the number of legs. Longer leg increases the probability to reach the goal, making more molecular spiders reach goal. And if the structure has more legs, it can cleave more substrates in the same time. Therefore, when the design of the fields is the same, robots with many legs are fast. This notion explained why the triangular prism was faster when comparing with the molecular spider.
Reference
(1) Fumiko Takagi et al. How protein thermodynamics and folding mechanisms are altered by the chaperonin cage: Molecular simulations, PNAS. 100, 11367 (2003)
(2) http://en.wikipedia.org/wiki/Langevin_equation
(3) http://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform
(4) Lund et al. Molecular robots guided by prescriptive landscapes, Nature. 465, 206 (2010)