User:Floriane Briere/Notebook/CHEM-496/2011/09/14
| File:BDLlogo notext ir.png Project name | |
|
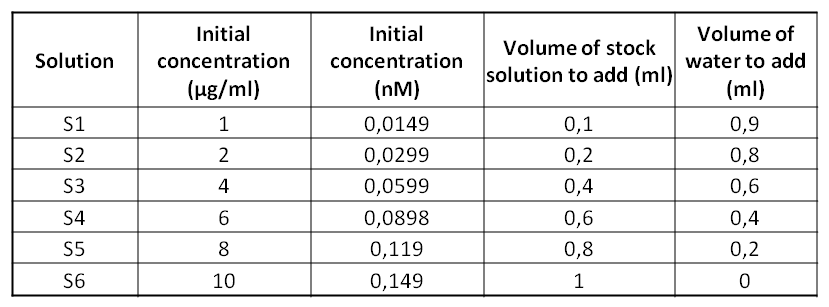
ObjectiveToday's experiment consists on performing a Bradford Assay technique which is going to allow us to determine the unknown proteins’ concentration of a solution. We are going to use 6 standards solutions of BSA whose concentrations are known. Then, thanks to a spectrophotometer, we’ll be able to determine the concentration of the MBP solution. Protocol
Results
To draw this curve, we add to take into account that the Bradford Assay was made with 5/6 diluted solutions (because we added 1ml of solution to 200µl of Bradford reagent). Red lines represent the Absorbance at 595nm of the 5/6000 diluted MPB solution. This curve allow us to determine the concentration of the MPB solution. We can calculate the unknown concentration thanks to the line’s equation (y = 2.1105x - 0.0204): Abs(595nm) = 2.1105 * concentration - 0.0204 => concentration = (0.44 + 0.0204)/2.1105 = 0.218nM So, the 5/6 diluted MPB solution has a concentration of 0.218nM. The pure MPB solution has a concentration of 0.261nM (0.218*(6/5) = 0.261nM). What are the final concentrations (in μg/mL of your standard solutions? Are they diluted from your original calculations. Your value for the concentration of MBP seems a bit low from where it should be. Also, you needed to take a spectrum of just MBP in water/buffer with NO Bradford Assay reagent. We need that so we can calculate ε. Matt Hartings 20:47, 20 September 2011 (EDT)
This curve is made with the standards solution and the 1/1000 diluted MPB solution (with bradford reagent)) measures. This curve is made with the 1/1000 diluted MPB solution (without Bradford reagent) measures.
According to Beer-Lambert law, Absorbance = molar absorptivity (L.mol^-1.cm^-1) * concentration (M) * length of the cuve (cm) So, molar absorptivity (ε) = Absorbance/(concentration (c)* length of the cuve (l)) We used the Absorbance of the 1/1000 MPB solution (without Bradford reagent) whose concentration is 29,16*10^-12M. And we know that l = 1cm
| |