Physics307L:People/Harriger/Lab 01: Measuring the Speed of Light
Summary
SJK 00:29, 13 October 2010 (EDT)

This is a very nice summary. I enjoyed reading it and could tell you learned a lot!
In this lab we measured the speed of light by timing how long it took for light to get from one point to another point and dividing that time by the distance between the points. We used an LED circuit to emit the light and a Photomultiplier tube (PMT) to detect the light. We could move the LED closer and farther from the PMT inside a cardboard tube approximately 2 meters long. We measured the voltages output from the PMT when the LED was between 0 and 100 cm from it. We moved the LED closer in increments of 20 cm, and measured the voltage for each distance 5 times. Using the average voltages over the 5 Trial sets, we made a linear fit graph of the voltage versus the distance using a least squares regression method. We obtained a conversion factor to change cm/V to cm/ns from taking into account the delay caused by the current traveling through wires of different lengths between our modules. By inverting the slope of the line and multiplying it by the conversion factor we obtained values for the speed of light.
When the Time Amplitude Converter (TAC) triggers at a fixed voltage, the time at which it triggers will be later for smaller amplitude pulses than for larger ones. This means it detects the larger amplitude pulses sooner than it should. In our set up, as the light source is moved closer to the Photomultiplier tube (PMT), the amplitude of the signal sent by the PMT increases. The effect of this is that at each progressively closer measurement, the PMT generates a larger amplitude pulse than at the measurement before, and hence the pulse output by the PMT triggers the TAC sooner than it should for the amount of distance traveled by the light. This is called time walk, and it is an important source of systematic error in particle physics. To make up for this, a polarizer is attached to the PMT that allows us to to adjust the amplitude manually in order to keep it constant for each measurement. We had to adjust the polarizer by hand for each distance at which we measured a voltage and gauge the amplitude on the oscilloscope by eye while we made the adjustment.
Error in our experiment could have come from systematic errors generated by using a meter stick to take distance measurements, by miscalibrations in our set up, or by not compensating for the time walk enough. Human error could have come from adjusting the polarizers by hand and matching the amplitude by eye, or in reading the distance.
- In this lab I worked with Brian P. Josey.
- These are my Detailed Lab Notes.

This is our set up. The oscilloscope is on the right, and the chassis is on the left. The long tube behind contains the PMT with the polarizer at the end behind the chassis, and the LED taped onto some meter sticks, so we can move it closer and farther from the PMT inside the long tube, on the other end.
Analysis
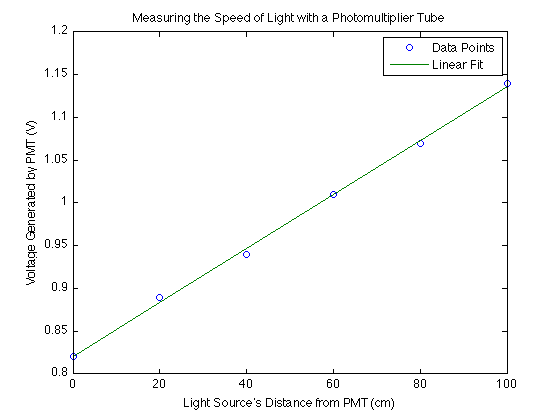
This is a linear fit model for the voltage as a function of the distance based on the average values of the velocity over our 5 Trial Sets. The graph was created with MATLAB 7.8 which uses a least squares method.
The equation for the linear fit is [math]\displaystyle{ y = .0032x + 0.8205 }[/math], so the slope is .0032 V/cm.
SJK 00:25, 13 October 2010 (EDT)

As you probably know by now, this is not correct--we've discussed in class a couple times how to produce the uncertainty using LINEST in linear regression.
The uncertainty in this slope is +/- the voltage point farthest from the linear fit subtracted from linear fit value for distance corresponding to that voltage point, all divided by the distance for that point: [math]\displaystyle{ +/-(0.94 - 0.9468)/40 = +/- 0.00017 }[/math] V/cm.
Inverting the slope, the slope plus the uncertainty, and the slope minus the uncertainty gives the average velocity, the minimum velocity, and the maximum velocity respectively.
Average Velocity: [math]\displaystyle{ 1/0.0032 = 312.5 }[/math] cm/V
Minimum Velocity: [math]\displaystyle{ 1/0.00337 = 296.7359 }[/math] cm/V
Maximum Velocity: [math]\displaystyle{ 1/0.00303 = 330.0330 }[/math] cm/V
From our initial measurement of the difference in voltage between two delay settings, we calculated the time delay to be 0.1 V/ns. This can be used to covert cm/V to cm/ns.
Average Velocity: [math]\displaystyle{ 312.5 * 0.1 = 31.25 }[/math] cm/ns
Minimum Velocity: [math]\displaystyle{ 296.7 * 0.1 = 29.67 }[/math] cm/ns
Maximum Velocity: [math]\displaystyle{ 330 * 0.1 = 33 }[/math] cm/ns
The accepted value from Wikipedia for the speed of light is 29.98 cm/ns.
SJK 00:28, 13 October 2010 (EDT)

I like how you propagate the uncertainty, using the minimum / maximum technique. That is good as we discussed in lecture after you did this. What's missing is a comparison to the accepted value. In your case, I'm not sure you estimated the uncertainty correctly (as noted above). However, ignoring that, what you want to do is compare whether it's likely that the accepted value for c is consistent with your range. In your case it is, though with Brian's analysis, it's more questionable.
I like your suggestions for better data if you were to repeat.
Conclusion
This is the first lab in which I attempted to quantify uncertainty or classify types of error. I learned about different kinds of error from and tried to follow the work of Alexandra Andrego in order to understand the propagation of uncertainty in my data. If I were to do this lab again I would measure the voltages at distances 5cm apart and take 10 measurements for each distance in order to increase the resolution and decrease the uncertainty of my data. I would also try to find a way to calibrate the set up. To improve this lab in the future, I would include very clear and concise instructions for obtaining the conversion factor and graphics showing what different parts of the oscilloscope reading represent.