IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/Results/2D Model2
From OpenWetWare
(Redirected from IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/2D Model2)
Introduction
Generalities
- The assumptions made Lotka-Volterra equation are very remote to the ones made during the derivation of our model. Consequently our model is very different from the pure Lotka-Volterra.
- We start bridging the gap between the two models by modifying the growth term of the prey population in Lotka-volterra
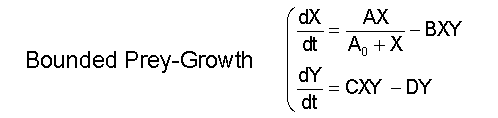
Physical interpretation of the equations
- The prey (AHL) production is limited by the limited number of promoters, which can be modelled by a Michaelis-Menten-like kinetics. For very small values of the prey-population (X) the growth can still be assumed proportional to the population (as with Lotka-Volterra). However, for larger populations it becomes constant as the system reaches saturation due to the limited number of promoters.
- For all the other terms of the system the assumptions made for Lotka-Volterra remain.
Basic Results on the Steady Points and Vector Field
Steady Points
- The Dynamical System has two stationary points
- - (0, 0), which is always a saddle point
- - (D/C, AC/(B(AoC+D)) which is always stable
Vector Field
- The resulting Vector Field is a slightly distorted version of the Vector Field of Lotka-Volterra:

Behaviour at Infinity
- It is easy to show that the trajectories remain bounded as time goes to infinity regardless of he choice of parameters.
- -We can therefore apply Poincare-Bendixson's theorem.
- -Because the system only has 2 steady points , one a saddle point the other a stable point we are sure the system will not oscillate.
- - For initial conditions (Xo,Yo) both non-null the trajectories will converge to the stable steady point
Typical Simulations
- The typical behaviour of the system (convergence to stable steady point) can be illustrated by the following simulation, and the corresponding time variations of the prey and predator populations are dampened oscillations


- Simulations using different initial conditions are assigned different colors (the open-end of the trajectories is the starting point). In the phase diagrams , red dots symbolise a steady points.
Conclusion
- The bounding of the predator growth has a dramatic effect on the system. The balance between the growth term of the preys and predators and their decay/degradations terms is broken.
- We cannot have any sustained oscillations anymore.