User:David K. O'Hara/Notebook/physics 307 lab/Electron Spin Resonance Lab
Theory
SJK 18:46, 25 October 2009 (EDT)

Good job on this lab & tackling a complicated setup. Very nice primary notebook & much better description of analysis this time. It was still not crystal clear to figure out your analysis, but definitely everything necessary was there so I could follow.
In this experiment I will be measuring the g sub s- quantity of the electron. I will do this by looking for the spin-flip transition of a free (unpaired)electron immersed in a magnetic field. A sample is placed in a uniform magnetic field, it is also wrapped inside a coil that is connected to an RF oscillator. The smaller magnetic field induced by the oscillator is at right angles to the uniform magnetic field.
The single electron of interest in the magnetic field, due to the magnetic dipole moment of the electron it can only align it's spin with the magnetic field in one of two ways, spin up or spin down. It will have energy Eo+/-gsμbB/2 with Eo the energy of the electron before the magnetic field was applied.
Resonance occurs when the frequency of the RF oscillator ν, such that the photon energy hν is equal to the energy between the two possible states of the electron. Therefore when :[math]\displaystyle{ h\nu = g_s \mu_B B \, }[/math] an electron in the lower state can absorb a photon and jump to the higher state.
Equipment
ESR probe unit.
Pair of Helmholtz Coils.
ESR adapter
Frequency Meter (Fluke 45 dual display multimeter)
HP 6236b Triple Output Power Supply (supply for the +-12 Volts for the ESR adapter)
Variac Autotransformer w5mt3
6.3 Volt transformer
Wavetek digital multimeter (DC ammeter)
Tektronix Oscilloscope TDS 1002
1000 μF capacitor
Homemade Phase Shifter Box
soar dc power supply model ps3630 (10 volt dc variable supply)
Safety
In addition to typical electrical shock hazards, this experiments requires the use of a large electrolytic capacitor, Special Care Must be taken to avoid running strictly AC current from the variac through the Cap or greater AC voltage than DC, this can result in the capacitor overheating and exploding.
On the second day of working with this lab, after a loose connection caused the DC power to be absent from the circuit, we blew the electrolytic capacitor. Once the smoke had cleared we put two capacitors wired in parallel instead of the single cap the setup called for and the circuit was much more stable.
Procedure
SJK 18:15, 25 October 2009 (EDT)

Excellent use of photos and diagrams!
Setting equipment up following procedure in the lab manual.
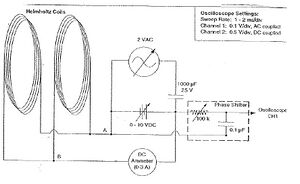
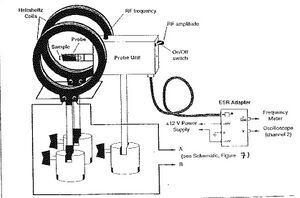
-
different shots of the apparatus setup
-
material sample (DPPH diphenyl-Pieryl-hydrazyl) and large and small coils
-
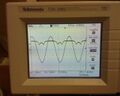
Ocilloscope readout showing resonance signal beginning to show
-
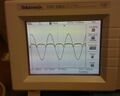
oscilloscope reading where current should be read of dmm
Data (Medium Coil)
| Res fq (MHz) | Current (A) |
|---|---|
| 25.013 | .461,.461, .452 |
| 30.003 | .542, .560, .551 |
| 35.020 | .641, .659, .641 |
| 40.041 | .731, .722, .731 |
| 45.090 | .839, .830, .830 |
| 50.313 | .902, 0.893, .911 |
| 55.092 | 1.002, 1.001, 1.010 |
| 60.046 | 1.101, 1.100, 1.101 |
| 65.019 | 1.181, 1.174, 1.173 |
| 70.010 | 1.264, 1.264, 1.264 |
SJK 18:17, 25 October 2009 (EDT)

Good idea to randomize before each measurement to try to make them independent and thus able to estimate random error.
I took three measurements for each resonance frequency, after each measurement I adjusted the current up until no trace of resonance showed on the scope and I moved the phase shifter so the curves would not line up the same and retook the measurement. Most of the measurement groups were quite tight giving me some hope that the measurements are accurate. Surprisingly, the data for the 70khz signal came out the same all three times. In fact, all the groupings where I crossed the one amp range on the dmm were remarkably similiar. Possibly, at current > than 1 amp the dmm loses some accuracy on the milliamp side to display the ones digit. I wish I could credit improved skill at measuring the points where the resonance values occur, but I don't think that's it.
data large coil)
| Res fq (MHz) | Current (A) |
|---|---|
| 19.901 | .371 |
| 21.066 | .398 |
| 23.083 | .425 |
| 25.067 | .471 |
| 27.008 | .497 |
| 30.027 | .552 |
| 32.050 | .596 |
| 34.038 | .623 |
I had to switch from a 5khz jump between measurements to a smaller step for the larger coil to get a decent range of frequency measurements as the coil would not generate a frequency higher than 34.5Khz
analysis
SJK 18:28, 25 October 2009 (EDT)

Looks like value of "R" is missing here (but is included in spreadsheet, which is good).
- To find the magnetic field between the Helmholtz coils, we had to calculate the magnetic field between the coils using the formula:
[math]\displaystyle{ \mathrm{B}=\frac{\mu\,{R}^{2}N I}{({R}^{2}+{x}^{2})^{3/2}} }[/math]
This derivation can be found on Wikipedia's page for Helmholtz coils
Which reduces to:
- [math]\displaystyle{ B = {\left ( \frac{4}{5} \right )}^{3/2} \frac{\mu_0 n I}{R} }[/math]
- [math]\displaystyle{ \mu_0\; }[/math] = 1.256 × 10-6 T·m·A-1
- N = the turns in each coil (320)
- I is the current through each coil.
To find gs
- [math]\displaystyle{ h\nu = g_s \mu_B B \, }[/math]
- [math]\displaystyle{ \nu\; }[/math] = the RF frequency
- [math]\displaystyle{ B\; }[/math] = the field at resonance
- [math]\displaystyle{ \mu_B\; }[/math] = the Bohr magneton = [math]\displaystyle{ e \hbar /2m_e }[/math] = 5.788 × 10^−9eV /G = 9.274 009 15(23) × 10-24 J•T-1
- The accepted value for gs=2.00232
For some reason my calculated g factors were off by a factor of 2, I don't know if this is due to the way current was measured, or the way the way the data was read from the scope(possibly looking at only half the actual period), but the data was good and putting a factor of two into the calculations the numbers make much more sense. I just don't have a justification for putting in that factor other than it brings the data into the reasonable realm from the way off. See comments in excel worksheet.
(Steve Koch 18:37, 25 October 2009 (EDT): For convenience, I'm copying comments over here. Dave says: "2 changes to data interpretation from the lab manual, when it shows the calculation for the energy splitting the lab manual uses B/2 for that calculation instead of B. When I used the lab manuals equation which had B by itself I was off by a factor of approximately 2, so I put in a 1/2 factor in the calculation of B. Second, the Linest function could not deal with h* freq and mu sub b * B in their raw form, it returned a slope of zero. I multiplied the data by 1e26 to give excel some range to work with. Even though it would calculate the graph the data interpretation function was not returning reasonable values.")SJK 18:37, 25 October 2009 (EDT)

I think the factor of B/2 in splitting is correct, since the electron has spin 1/2, right? But the difference between the two energy levels is twice the value listed (because it goes from -1/2 to +1/2 for total change of 1). It is really difficult to see exactly where you put your factor of 2 "fudge factor," since you seem to have just hard coded it in there. I think the answer is this: I is supposed to be "the current to EACH coil." When I look at your circuit diagram, you are measuring the total current coming out of the power supply, but then you are splitting that current in parallel into the two coils (and thus it's a factor of 2 less than you measure). Is that right?