Physics307L:People/Muehlmeyer/Formal Final
Approximating the Speed of Light via LED Emmission
Author: Justin Muehlmeyer
Experimentalists: Justin Muehlmeyer and Alexander Barron
University of New Mexico
Department of Physics and Astronomy Junior Lab November 2008
jmuehlme@unm.edu
Abstract
Is it possible to directly measure the speed of light over a distance of less than two meters? To approximate the speed of light we measured the "flight time" of pulses of light emitted by a light emitting diode by measuring the time difference between LED emission and PMT reception of the light signal down a tube via a time amplitude convertor (TAC). By varying the distance the light signal travels we plot distance vs. flight time and use the linear-least squares method to approximate the slope of our data, which gives us the speed of light. We found that our best approximation to the accepted value of 2.99 X 108 m/s was 2.91 ± .38 X 108 m/s, which came from large variations in distance and from using the "time walk" correction that accounts for the changing intensity of the light as the LED distance approaches the PMT.
Introduction
The speed of light is certainly one of the most researched constants in science. Before Galileo, the speed of light was thought to be infinite, arriving at the eye at the same time it left the source. Numerous experimental methods have been used since the first attempt in 1676 by Olaus Roemer (see figure 1) to measure its speed thus showing that light is indeed finite.
At this time light was thought to be similar to sound in that it propagates through some medium. This hypothetical medium was called the "ether". Down the road, this ether led to theoretical inconsistencies with Galilean Relativity and vector addition of velocities. This was shown in the famous 1881 Michelson-Morley experiment that disproved the existence of the ether by showing that the expected "ether wind" created by the earth propagating through the ether in fact has no effect on light beams (A.A Michelson, 1881).
Michelson later spent a considerable amount of time later in his career measuring the speed of light itself. He used a rotating mirror and prism some tens of miles away from the ligh source and measured the speed of light to be 299,794 ± 11 km/s (Michelson, 1935).

By the early 19th century light had been established as a wave, much thanks to the theoretical and experimental accomplishments of Thomas Young and Augustine (Ohanian, 2001). Also, Maxwell's electromagnetic theory had allowed for the determination of the speed of light to be done indirectly from the magnetic permeability and electric permitivity of free space. This allowed for the Rosa and Dorsey experiment of 1907 which obtained a speed of 299,788 km/s.
In 1905, Einstein's Special Theory of Relativity emerged out of the rubbles of the ether, giving new theoretical grounds for the measurement of the speed of light. Einsteins relativity is structured on two postulates. First that the laws of physics in one coordinate frame also hold in another coordinate frame moving with uniform velocity with repsect to it. Second that the velocity of light is independent of the velocity of the source (Hodgson, 1978).
Since then the speed of light has been validated in numerous ways. One example comes from the war era, with the advent of microwave cavities. In 1935, Louis Essen and A.C. Gordon Smith used a microwave cavity and measured the speed of light to be 299,792 ± 3 km/s. This was done by establishing the frequency for a variety of modes of microwaves in a cavity, which of course according to Maxwell's Electromagnetic theories travel at the speed of light. Knowledge of the associated frequencies allowed them to approximate the speed of light (Wikipedia 2008).
Today the speed of light is measured with advanced optical lasers.
Other interesting examples include the "space echo" of astronauts on the moon. The delay of communication from the astronauts during the 1972 Apollo 16 mission provided an approximate determination of the speed of light (Keeports, 2006).
Since 1983 the metre has been defined by international agreement as the length of the path travelled by light in vacuum during a time interval of 1/299,792,458 of a second. This makes the speed of light exactly 299,792.458 km/s, which is the official accepted value of the speed of light constant c.
In this experiment we use a very simple method to determine the speed of light in air, and achieved results within 3 % of the accepted value. We approximated the speed of light by measuring the time difference between LED emission and PMT reception of a light signal down a tube via a time amplitude convertor (TAC). By varying the distance the light signal travels we plot distance vs. flight time and use the linear-least squares method to approximate the slope of our data, which gives us the speed of light.
Methods
Set Up
A long cardboard tube has the LED on one end pointing in at the PMT (Perfection Mica Company N-134 ) receiving its signals on the other end. The LED Cycles on and off at around 10KHz depending on the voltage applied (recommended voltage is around 200 volts DC). The PMT is powered by a high voltage power source at about 1900 Volts. The LED is strapped to 3 meter sticks binded by tape so that we can push the LED down the tube and measure the change in distance from its initial point. The tube is a cardboard tube wide enough to fit the PMT on one end and LED on the other. The PMT and LED each have a polarizer attached to their fronts, so that as we push the LED down the tube we can rotate the PMT on the other end to maintain a constant intensity (see segment on intensity and time walk below). The anode of the PMT is connected to the input on the delay module and to channel 1 of the digital oscilloscope (Tektronics TDS 1002). Refer to figure 2.

The LED is connected to its power supply via a BNC cable. We have the LED power supply outputing 190 V. The PMT is connected via a BNC to its high voltage source outputing at 1900 V.
To measure the time difference between LED emission and PMT reception we have a time amplitude converter (TAC) which converts the time difference of its inputs into a voltage that is proportional to that time difference. The two BNC inputs are labeled the "start" time from LED emission, and the "stop" time from PMT reception through the delay module. The output ratio of the time difference between the two inputs is 10 V = 50 nS, which we read on the digital oscilloscope in channel 2.
Time Walk
Since our TAC triggers at a fixed voltage, its triggering time occurs later for small incoming amplitudes then larger ones. This created an issue because as we pushed the LED in closer to the PMT, the PMT signal increased in amplitude and the "time walk" problem then becomes a large source of systematic error. To avoid this issue we must maintain a constant PMT signal by using the polarizers to maintain constant intensity on the PMT.
The intensity was kept constant by rotating the PMT by slight amounts which rotated the polarizer covering its "lens". The polarizer "filters" or "cuts" the incoming light's electric field based on the angle that the polarizer film molecules are aligned. There is a point (or angle rather) when the polarizer cuts the incoming light entirely, and no voltage can be seen from he TAC at all. This means the alignment of the polarizer with the incoming electric field from the LED is perindicular. This is found to be of great importance, if we don't maintain a constant intensity for the PMT reception then our actual time difference will be skewed due to the fact that the TAC is receiving more signals from the PMT then it should.
Procedure and Data Methods
We varied the distance between the LED module and the photomultiplier tube, taking voltage measurements from the oscilloscope. Each trial was done with the following method:
Trial 1) Large and increasing individual Δx over large total Δx.
Trial 2) Small, constant individual Δx over small total Δx.
Trial 3) Large, constant individual Δx over large total Δx.
Trial 4) Medium Δx with no time walk correction.
For each Δx, we move the LED-pulse generator farther away from the PMT in specified intervals.
The raw signal from the TAC when the oscilloscope is in "sample" mode is very turbulent and quite impossible to read. The best method for data acquisition on the digital oscilloscope is using the "average" function which takes an average of the data over a set period of time. The deviation then is measured by eye, based on the fluctations of the signal from that average.
Plotting the distance vs. time and taking the slope of the line best fit line of these points via the least-squares method produced an estimate for the speed of light.
Analysis Methods
According to Taylor (see references) we determine the coefficients of a best fit linear line [math]\displaystyle{ y = A + Bx }[/math] by the relations below.
- [math]\displaystyle{ A=\frac{\sum x_i^2 \sum y_i - \sum x_i \sum x_i y_i}{\Delta_{fixed}} }[/math] [math]\displaystyle{ \mbox{,}~~~~~~~~~~~~~~~~~ \sigma_a^2 = \frac{\sigma_y^2}{\Delta_{fixed}} \sum x_i^2 }[/math]
- [math]\displaystyle{ B=\frac{N\sum x_i y_i - \sum x_i \sum y_i}{\Delta_{fixed}} }[/math] [math]\displaystyle{ \mbox{,}~~~~~~~~~~~~~~~~~ \sigma_b^2 = N \frac{\sigma_y^2}{\Delta_{fixed}} }[/math]
- [math]\displaystyle{ \Delta_{fixed}=N \sum x_i^2 - \left ( \sum x_i \right )^2 }[/math]
The uncertainties in these values create an upper and lower bound for our values of the speed of light. The maximum slope is produced by adding the mean slope and the standard error of the slope. The minimum slope is the mean slope minus the standard error of the slope. The maximum and minimum y-intercepts, are the mean y-intercept plus and minus the standard error of the y-intercept, respectively.
By forcing the linear best fit line to the y-intercepts we can attain our maximum and minimum values for the speed of light when the least-squares method is implemented.
See results below.
My data analysis Excel workesheet can be accessed here:
File:Speed of Light Data Analysis Formal.xls
Tables and Results
Trial 1 Data: Distance changes increased rapidly from the initial point.
Trial 2 Data: Small changes in distance.
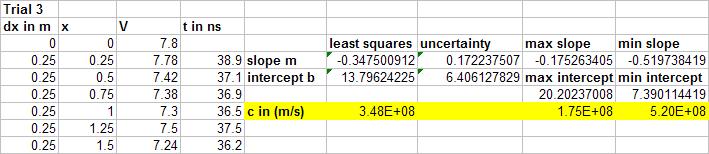
Trial 3 Data: Large changes in distance, but not as large as trial 1.
Trial 4 Data: was to check the importance of time walk correction. We did not use the polarizers here to correct for the changing intensity.
- All voltages were measured to have an uncertainty of ± 0.02 V due to the oscilloscope reading. This is accounted for in our data plots where on our time axis we will see error bars of ± 0.1 nS. This comes from oour TAC ratio of 10 V = 50 nS.
| Trial | Graphic Representation | Trial | Graphic Representation |
|
Trial 1: rapid and largest distance changes
Upper Error Bound:
Lower Error Bound:
|
|
Trial 2: small and constant distance changes
Upper Error Bound:
Lower Error Bound:
|
|
|
Trial 3: larger and constant distance changes
Upper Error Bound:
Lower Error Bound:
|
|
Trial 4: no time walk correction
Upper Error Bound:
Lower Error Bound:
|
|
Conclusion
Our best approximation to the true value was trial 1 with a value of [math]\displaystyle{ {c}=2.91 \pm .38\cdot 10^{8}\frac{m}{s} }[/math].
Our approximation has a percent error from the actual of only 2.7 %, showing that our method was systematically accurate, and that in fact the speed of light can be reasonably determined by light emission down something as simple as a cardboard tube.
The results show the importance of large changes in distance of the LED, and the necessity of the time walk correction. In this way we see where our largest sources of error comes from: inaccurate measurments on the meter sticks pushing the LED into the tube, and keeping the reference voltage constant for the time walk correction as we push the LED in.
I could imagine that greater accuracy in this final result, or at least greater consistency within trials, could be attained by more precise ways of data acquisition. The greatest source of error in this experiment came from the oscilloscope readings, during which one must keep the reference voltage as constant as possible while attempting to determine an average value for the turbulent incoming signal from the PMT. Maybe the experiment can be further developed to have better monitoring of the reference voltage, and to have a computer measure the voltages from the TAC.
In conclusion, even with these large sources of systematic error, we obtained the speed of light using a cardboard tube.
Acknowledgements
Thanks to my lab partner Alexander "Der" Barron, our lab professor Dr. Steven Koch, and our lab TA, Aram Gragossian.
References
Figure 1 from: Gibbs, Phillip. "How is the speed of light measured?", 1997, UseNet Physics FAQ Website [1]
Figure 2 from: Smith, J.J. and Martin, Kyle, "Electronically Measuring the Flight Time of Light", 2007.
Gold, Michael. 2006. PHYSICS 307L: Junior Laboratory. The University of New Mexico, Dept. of Physics and Astronomy. [2]
Taylor, John R. 1997. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books, 2 ed.
Ohanian, Hans. Special Relativity: A Modern Introduction. 2001. Sections 1.5, 1.6.
Michelson, A. A., American Journal of Science 122,120 (1881).
Michelson, A. A., Pease, F. G., & Pearson, F. (1935). Measurement of the velocity of light in a partial vacuum. Astrophysical Journal, 82.
Hodgson, P. E. "Speed of light and relativity." Nature 271 (1978): 13. Nature
Wikipedia Speed of Light Article 2008 [3]
Estimating the Speed of Light from Earth-Moon Communication. David Keeports, Phys. Teach. 44, 414 (2006), DOI:10.1119/1.2353576. [4]